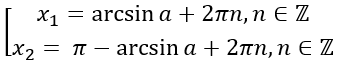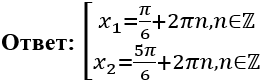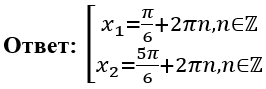Простейшие тригонометрические уравнения

Простейшие тригонометрические уравнения

Причем на месте $x$ может стоять любое выражение, содержащее $x$, а правая часть уравнения является числом.

Каждое простейшее уравнение имеет свою формулу решения, но, чтобы их не пришлось заучивать, можно использовать метод решения через тригонометрический круг.

АЛГОРИТМ РЕШЕНИЯ ЧЕРЕЗ ТРИГОНОМЕТРИЧЕСКИЙ КРУГ:

1. Рисуем тригонометрический круг.
2. Отмечаем известное значение тригонометрической функции на соответствующей оси.
3. Через полученное значение на оси проводим прямую для:

$\sin x$ – горизонтальную

$\cos x$ – вертикальную

$\text{tg\ x}$, $\text{ctg\ x}$ – через начало координат до пересечения с кругом.

4. Записываем полученные значения $\arcsin/\arccos/\ \text{arctg}/\ \text{arcctg}$ + период:

$2\pi n,\ n\mathbb{\in Z} - полный\ круг$

$\pi n,\ n\mathbb{\in Z} - половина\ круга$

УРАВНЕНИЯ ВИДА $\mathbf{\sin}\mathbf{\text{x\ }}\mathbf{= a}$:

Решением такого вида уравнения является:

$\ x = \left( - 1 \right)^{n}\arcsin a + \pi n,\ n \in Z$

Она объединяется в себя две другие:

Такие же корни уравнения получаются при нахождении их через тригонометрический круг.

Решите уравнение:

$\sin x = \ \frac{1}{2}$

Первый способ. Через формулу:

1. Первая серия корней уравнения будет:

$x_{1} = \arcsin\frac{1}{2} + 2\pi n,n\mathbb{\in Z}$

$x_{1} = \frac{\pi}{6} + 2\pi n,\ n\mathbb{\in Z}$

2. Вторая серия корней:

$x_{2} = \ \pi - \frac{\pi}{6} + 2\pi n,\ n\mathbb{\in Z}$

$x_{2} = \frac{5\pi}{6} + 2\pi n,\ n\mathbb{\in Z}$

3. Записываем в ответ либо две серии аргументов сразу, либо одну, заключённую в общую формулу:

$x = \left( - 1 \right)^{n}\frac{\pi}{6} + \pi n,\ n \in Z$

Второй способ. Через тригонометрический круг:

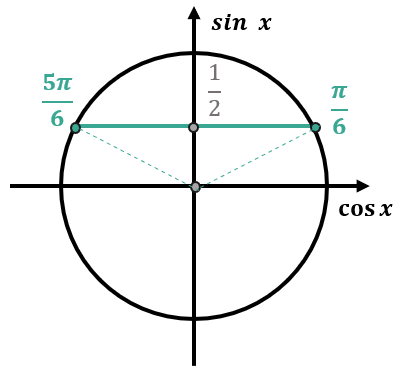
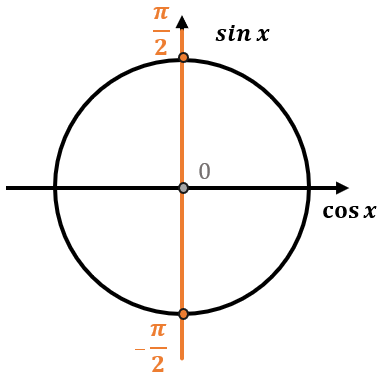
1. Рисуем тригонометрический круг и отмечаем на оси синусов значение $\sin x = \frac{1}{2}.$
2. Для синуса проводим горизонтальную прямую, параллельную оси Ох, проходящую через точку $\sin x = \frac{1}{2}.$
3. В точках пересечения этой прямой с окружностью и будут находиться корни уравнения.
4. Записываем все получившиеся корни с учетом периода.

При использовании тригонометрического круга мы получили те же значения, что и при использовании формул.

УРАВНЕНИЯ ВИДА $\mathbf{\cos}\mathbf{\text{x\ }}\mathbf{= a}$:

Решением такого вида уравнения является:

$x = \pm \arccos 0 + 2\pi n,\ n\mathbb{\in Z}$

Решите уравнение:

$\cos x = 0$

Первый способ. Через формулу:

Для косинуса существует лишь одна формула, в которую включены уже две серии корней:

$x = \pm \ \frac{\pi}{2} + 2\pi n,\ n\mathbb{\in Z}$

Ответ: $x = \pm \ \frac{\pi}{2} + 2\pi n,\ n\mathbb{\in Z}$.

Второй способ. Через тригонометрический круг:

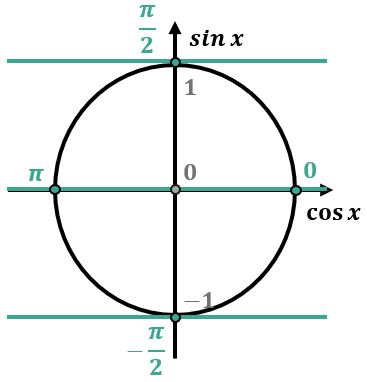
1. Рисуем тригонометрический круг и отмечаем на оси косинусов значение $\cos x = 0$
2. Для косинуса проводим вертикальную прямую, параллельную оси Оу, проходящую через точку $\cos x = 0$
3. В данном случае эта прямая совпадет с осью Оу и пересекает окружность в диаметре.
4. Записываем получившийся корень с учетом периода. В данном случае можем записать ответ как формулу в первом методе решения, а можем записать его как один из углов + период π, т.к. каждый следующий корень уравнения повторяется через пол-оборота.

Ответ: $x = \frac{\pi}{2} + \pi n,\ n\mathbb{\in Z}$

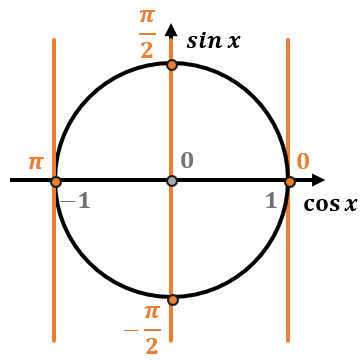
ОСОБЫЕ СЛУЧАИ:

Пример №2 является примером особого случая, когда значение тригофункции попадает на пересечения оси Ох или Оу с окружностью.

К особым случаям относятся следующие уравнения:

Синус:

1. $\sin x = 0$:

$x = \pi n,\ n\mathbb{\in Z}$

2. $\sin x = 1$:

$x = \frac{\pi}{2} + 2\pi n,\ n\mathbb{\in Z}$

3. $\sin x = \ –1$:

$x = \ –\frac{\pi}{2} + 2\pi n,\ n\mathbb{\in Z}$

Косинус:

1. $\cos x = 0$:

$x = \frac{\pi}{2} + \pi n,\ n\mathbb{\in Z}$

2. $\cos x = 1$:

$x = 2\pi n,\ n\mathbb{\in Z}$

3. $\cos x = \ –1$:

$x = \pi + 2\pi n,\ n\mathbb{\in Z}$

УРАВНЕНИЯ ВИДА $\mathbf{tg\ x = a}$ и $\mathbf{c}\mathbf{tg\ x = a}$:

Решением этих уравнения является:

$tg\ x = a$

$x = arctg\ a + \pi n,\ n\mathbb{\in Z}$

$ctg\ x = a$

$x = arcctg\ a + \ \pi n,\ n\mathbb{\in Z}$

Решите уравнение:

$\text{tg\ x} = \sqrt{3}$

Первый способ. Через формулу:

Запишем формулу для нахождения корней для тангенса:

$x = arctg\ \sqrt{3} + \pi n,\ n\mathbb{\in Z}$

$x = \frac{\pi}{3} + \pi n,\ n\mathbb{\in Z}$

Это и есть ответ к данному уравнению.

Ответ: $x = \frac{\pi}{3} + \pi n,\ n\mathbb{\in Z}$

Второй способ. Через тригонометрический круг:

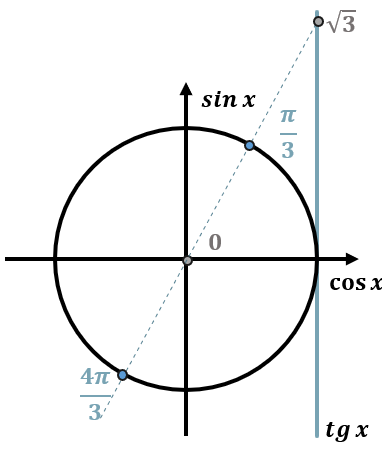
1. Рисуем тригонометрический круг и отмечаем на вертикальной оси тангенсов значение $tg\ x = \sqrt{3}$.
2. Для тангенса проводим прямую через начало координат, пока она второй раз не пересечет окружность.
3. В точках пересечения этой прямой с окружностью и будут находиться корни уравнения.
4. Записываем все получившиеся корни с учетом периода.

Ответ: $x = \frac{\pi}{3} + \pi n,\ n\mathbb{\in Z}$