Правила дифференцирования

Название производной происходит от слова «произведенная», т.е. образованная от другой величины. Производная характеризует темп изменения функции.

Процесс определения производной какой-либо функции называется дифференцированием. Если говорить совсем просто, то для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию.

Формулы нахождения производных основных функций

Число, степенная функция, функция с коэффициэнтом

Функция Формула	Пример
Число $c' = \ 0$	$7' = \ 0$ Важно! $(ln\ 7)'\ = 0$ $\pi^{'} = 0$ Так как это число, а не функция
Степенная функция $\left( x^{n} \right)^{'} = \ n \bullet \ x^{n - 1}$	$\left( x^{7} \right)^{'} = 7 \bullet x^{7 - 1} = 7 \bullet x^{6}$
Частный случай — квадратный корень $(\sqrt{x})'\ = \frac{1}{2\sqrt{x}}$	Вывод формулы: $\left( \sqrt{x} \right)^{'} = \left( x^{\frac{1}{2}} \right)^{'} = \frac{1}{2}x^{\frac{1}{2} - 1} = \frac{1}{2}x^{- \frac{1}{2}} = \frac{1}{2\sqrt{x}}$
Частный случай — обратная функция $\left( \frac{1}{х} \right)^{'} = - \frac{1}{x^{2}}$	Вывод формулы: $\left( \frac{1}{х} \right)^{'} = \left( x^{- 1} \right)^{'} = - 1 \bullet x^{- 1 - 1} = - \frac{1}{x^{2}}$
Производная от функции, умноженной на коэффициент $\left( c \bullet f\left( x \right) \right)^{'} = c \bullet f'(x)$	$\left( 7x \right)^{'} = 7 \bullet x^{'} = 7 \bullet 1 = 7$ $\left( 3x^{7} \right)^{'} = 3 \bullet {(x}^{7})' = 3 \bullet 7 \bullet x^{7 - 1} = 21 \bullet x^{6}$

Функция

Формула

Пример

Число

$c' = \ 0$

$7' = \ 0$

Важно!

$(ln\ 7)'\ = 0$

$\pi^{'} = 0$

Так как это число, а не функция

Степенная функция

$\left( x^{n} \right)^{'} = \ n \bullet \ x^{n - 1}$

\left( x^{7} \right)^{'} = 7 \bullet x^{7 - 1} = 7 \bullet x^{6}

Частный случай — квадратный корень

$(\sqrt{x})'\ = \frac{1}{2\sqrt{x}}$

Вывод формулы:

$\left( \sqrt{x} \right)^{'} = \left( x^{\frac{1}{2}} \right)^{'} = \frac{1}{2}x^{\frac{1}{2} - 1} = \frac{1}{2}x^{- \frac{1}{2}} = \frac{1}{2\sqrt{x}}$

Частный случай — обратная функция

$\left( \frac{1}{х} \right)^{'} = - \frac{1}{x^{2}}$

Вывод формулы:

$\left( \frac{1}{х} \right)^{'} = \left( x^{- 1} \right)^{'} = - 1 \bullet x^{- 1 - 1} = - \frac{1}{x^{2}}$

Производная от функции, умноженной на коэффициент

$\left( c \bullet f\left( x \right) \right)^{'} = c \bullet f'(x)$

$\left( 7x \right)^{'} = 7 \bullet x^{'} = 7 \bullet 1 = 7$

$\left( 3x^{7} \right)^{'} = 3 \bullet {(x}^{7})' = 3 \bullet 7 \bullet x^{7 - 1} = 21 \bullet x^{6}$

Производная от показательно – степенной и логарифмической функций

Показательно-степенная функция $\left( a^{x} \right)^{'} = a^{x} \bullet \ln a$	$\left( 7^{x} \right)^{'} = 7^{x} \bullet \ln 7$
Частный случай показательно-степенной функции — основание е (экспонента) $\left( e^{x} \right)^{'} = e^{x}$	Вывод формулы: $\left( e^{x} \right)^{'} = e^{x} \bullet \ln{e = e^{x} \bullet 1 = e^{x}}$
Логарифмическая функция ${{(log\ }_{a}x)' = \frac{1}{x \bullet \ln a}}_{\ }$	${(\log\ }_{7}x)' = \frac{1}{x \bullet \ln 7}$
Частный случай логарифмической функции —с натуральным логарифмом (основание логарифма — е) $(\ln x)' = \frac{1}{x}$	Вывод формулы: $\left( \ln x \right)^{'} = \frac{1}{x \bullet \ln e} = \frac{1}{x \bullet 1} = \frac{1}{x}$

Показательно-степенная функция

$\left( a^{x} \right)^{'} = a^{x} \bullet \ln a$

\left( 7^{x} \right)^{'} = 7^{x} \bullet \ln 7

Частный случай показательно-степенной функции — основание е (экспонента)

$\left( e^{x} \right)^{'} = e^{x}$

Вывод формулы:

$\left( e^{x} \right)^{'} = e^{x} \bullet \ln{e = e^{x} \bullet 1 = e^{x}}$

Логарифмическая функция

${{(log\ }_{a}x)' = \frac{1}{x \bullet \ln a}}_{\ }$

{(\log\ }_{7}x)' = \frac{1}{x \bullet \ln 7}

Частный случай логарифмической функции —с натуральным логарифмом (основание логарифма — е)

$(\ln x)' = \frac{1}{x}$

Вывод формулы:

$\left( \ln x \right)^{'} = \frac{1}{x \bullet \ln e} = \frac{1}{x \bullet 1} = \frac{1}{x}$

Производная от тригонометрических функций

Синус $(\sin{x)' = cos\ x}$	-
Косинус $(\cos{x)' = - sin\ x}$	-
Тангенс $(\text{tg}{x)' = \frac{1}{\cos^{2}x\ }}$	Вывод формулы: $\left( \text{tg}x \right)^{'} = \left( \frac{\sin x}{\cos x} \right)^{'} = \frac{\left( \sin x \right)^{'} \bullet \cos x - \sin x \bullet \left( \cos x \right)^{'}}{\cos^{2}x} = \frac{\cos x \bullet \cos x - \sin x \bullet ( - \sin{x)}}{\cos^{2}x} = \frac{\cos^{2}x + \sin^{2}x}{\cos^{2}x} = \frac{1}{\cos^{2}x\ }$
Котангенс $(\text{ctg}{x)' = - \frac{1}{\sin^{2}x\ }}$	Вывод формулы: $\left( \text{ctg}x \right)^{'} = \left( \frac{\cos x}{\sin x} \right)^{'} = \frac{\left( \cos x \right)^{'} \bullet \sin x - \cos x \bullet \left( \sin x \right)^{'}}{\sin^{2}x} = \frac{- \sin x \bullet \sin x - \cos x \bullet \cos x}{\sin^{2}x} = \frac{{- \sin}^{2}x - \cos^{2}x}{\sin^{2}x} = \frac{- 1 \bullet \cos^{2}x + \sin^{2}x}{\sin^{2}x\ } = - \frac{1}{\sin^{2}x\ }$

Синус

$(\sin{x)' = cos\ x}$

Косинус

$(\cos{x)' = - sin\ x}$

Тангенс

$(\text{tg}{x)' = \frac{1}{\cos^{2}x\ }}$

Вывод формулы:

$\left( \text{tg}x \right)^{'} = \left( \frac{\sin x}{\cos x} \right)^{'} = \frac{\left( \sin x \right)^{'} \bullet \cos x - \sin x \bullet \left( \cos x \right)^{'}}{\cos^{2}x} = \frac{\cos x \bullet \cos x - \sin x \bullet ( - \sin{x)}}{\cos^{2}x} = \frac{\cos^{2}x + \sin^{2}x}{\cos^{2}x} = \frac{1}{\cos^{2}x\ }$

Котангенс

$(\text{ctg}{x)' = - \frac{1}{\sin^{2}x\ }}$

Вывод формулы:

$\left( \text{ctg}x \right)^{'} = \left( \frac{\cos x}{\sin x} \right)^{'} = \frac{\left( \cos x \right)^{'} \bullet \sin x - \cos x \bullet \left( \sin x \right)^{'}}{\sin^{2}x} = \frac{- \sin x \bullet \sin x - \cos x \bullet \cos x}{\sin^{2}x} = \frac{{- \sin}^{2}x - \cos^{2}x}{\sin^{2}x} = \frac{- 1 \bullet \cos^{2}x + \sin^{2}x}{\sin^{2}x\ } = - \frac{1}{\sin^{2}x\ }$

Производная от обратных тригонометрических функций

Арксинус $(\arcsin{x)' = \frac{1}{\sqrt{1 - x^{2}}}}$	Арктангенс $(\text{arctg}{x)' = \frac{1}{1 + x^{2}\ }}$
Арккосинус $({\text{arc}\cos}{x)' = - \frac{1}{\sqrt{1 - x^{2}}}}$	Арккотангенс $(\text{arcctg}{x)' = - \frac{1}{1 + x^{2}\ }}$

Арксинус

$(\arcsin{x)' = \frac{1}{\sqrt{1 - x^{2}}}}$

Арктангенс

$(\text{arctg}{x)' = \frac{1}{1 + x^{2}\ }}$

Арккосинус

$({\text{arc}\cos}{x)' = - \frac{1}{\sqrt{1 - x^{2}}}}$

Арккотангенс

$(\text{arcctg}{x)' = - \frac{1}{1 + x^{2}\ }}$

Производная от суммы, произведения и частного функций

Сумма функций $\left( f\left( x \right) + g\left( x \right) \right)^{'} = f'\left( x \right) + g'\left( x \right)$	$\left( 7^{x} + 7 \right)^{'} = {(7^{x})}^{'} + 7' = 7^{x} \bullet \ln 7$
Произведение функций $\left( f\left( x \right) \bullet g(x) \right)^{'} = f^{'}\left( x \right) \bullet g\left( x \right) + f(x) \bullet g'\left( x \right)$	$\left( x^{7} \bullet \cos x \right)^{'} = \left( x^{7} \right)^{'} \bullet \cos x + x^{7} \bullet \left( \cos x \right)^{'} = 7 \bullet x^{6} \bullet \cos{x + x^{7} \bullet ( - \sin{x)}} = 7 \bullet x^{6} \bullet \cos{x - x^{7} \bullet \sin x}$
Частное функций $\left( \frac{f\left( x \right)}{g\left( x \right)} \right)^{'} = \frac{f^{'}(x) \bullet g\left( x \right) - f(x) \bullet g'\left( x \right)}{g^{2}\left( x \right)}$	$\left( \frac{x^{7}}{\cos x} \right)^{'} = \frac{\left( x^{7} \right)' \bullet \cos x - x^{7} \bullet (\cos x)'}{\cos^{2}x} = \frac{7 \bullet x^{6} \bullet \cos{x - x^{7} \bullet ( - \sin{x)}}}{\cos^{2}x} = \frac{7 \bullet x^{6} \bullet \cos{x + x^{7} \bullet \sin x}}{\cos^{2}x}$

Сумма функций

$\left( f\left( x \right) + g\left( x \right) \right)^{'} = f'\left( x \right) + g'\left( x \right)$

\left( 7^{x} + 7 \right)^{'} = {(7^{x})}^{'} + 7' = 7^{x} \bullet \ln 7

Произведение функций

$\left( f\left( x \right) \bullet g(x) \right)^{'} = f^{'}\left( x \right) \bullet g\left( x \right) + f(x) \bullet g'\left( x \right)$

\left( x^{7} \bullet \cos x \right)^{'} = \left( x^{7} \right)^{'} \bullet \cos x + x^{7} \bullet \left( \cos x \right)^{'} = 7 \bullet x^{6} \bullet \cos{x + x^{7} \bullet ( - \sin{x)}} = 7 \bullet x^{6} \bullet \cos{x - x^{7} \bullet \sin x}

Частное функций

$\left( \frac{f\left( x \right)}{g\left( x \right)} \right)^{'} = \frac{f^{'}(x) \bullet g\left( x \right) - f(x) \bullet g'\left( x \right)}{g^{2}\left( x \right)}$

\left( \frac{x^{7}}{\cos x} \right)^{'} = \frac{\left( x^{7} \right)' \bullet \cos x - x^{7} \bullet (\cos x)'}{\cos^{2}x} = \frac{7 \bullet x^{6} \bullet \cos{x - x^{7} \bullet ( - \sin{x)}}}{\cos^{2}x} = \frac{7 \bullet x^{6} \bullet \cos{x + x^{7} \bullet \sin x}}{\cos^{2}x}

Сложная функция

Сложная функция — это когда внутри функции находится другая функция. То есть аргументом функции является другая функция. Как понять, что функция сложная: если в функции вместо икс стоит что-то другое — это сложная функция.

Например:

$\cos\text{x\ }$ — простая функция	$\cos\sqrt{x}$ — сложная функция: внутри функции косинуса стоит функция корня
$e^{x}$ — простая функция	$e^{2x - 7}$ — сложная функция: внутри показательно-степенной функции стоит линейная функция $\ 2x - 7$

Общая формула:

$(f\left( g\left( x \right) \right)' = f'(g) \bullet g'(x)$

Что она означает: мы берем производную от внешней функции, сохраняя ее аргумент таким, какой он был (то есть сохраняем ту функцию, которая стояла внутри), а потом умножаем ее на производную внутренней функции.

Примеры:

$\cos{(3x - 2)}$

Косинус — внешняя функция, сначала берем производную от нее

$f^{'}\left( g \right) = (\cos{(3x - 2))' =} - \sin{(3x - 2)}$

Обратите внимание, что внутренняя функция g = 3x – 5 не изменилась, её мы не трогаем. Отдельно находим от нее производную.

$g^{'}\left( x \right) = \left( 3x - 2 \right)^{'} = 3$

Теперь перемножим функции по формуле:

${(cos}{(3x - 2))' =} - \sin{(3x - 2)} \bullet 3$

$\log_{12}{(x^{2})}$

Внешняя функция логарифмическая, сначала берем производную от нее

$f^{'}\left( g \right) = (\log_{12}{(x^{2}))' =}\frac{1}{x^{2} \bullet \ln 12}$

Внутренняя функция g = x² пока не изменилась. Отдельно находим от нее производную:

$g^{'}\left( x \right) = \left( x²\ \right)^{'} = 2x$

Теперь перемножим функции по формуле:

${(\log_{12}\left( x^{2} \right))}^{'} = \frac{2x}{x^{2} \bullet \ln 12}$

$4^{x^{2} - 2x + 7}$

Внешняя функция логарифмическая, сначала берем производную от нее

$f^{'}\left( g \right) = \left( 4^{x^{2} - 2x + 7} \right)^{'} = 4^{x^{2} - 2x + 7} \bullet \ln 4$

Внутренняя функция g = x² пока не изменилась. Отдельно находим от нее производную:

$g^{'}\left( x \right) = \left( x^{2} - 2x + 7\ \right)^{'} = 2x - 2$

Теперь перемножим функции по формуле:

${(4^{x^{2} - 2x + 7})}^{'} = 4^{x^{2} - 2x + 7} \bullet \ln 4 \bullet (2x - 2)$

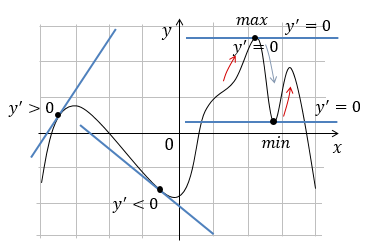
Анализ функций

Геометрический смысл производной: значение производной в точке равно тангенсу угла наклона (коэффициент k в уравнении) касательной, проведенной в данной точке.

$f^{'}\left( x_{0} \right) = tg\ \alpha = k$

Отсюда можно сделать несколько выводов о том, как можно анализировать функцию с помощью производной:

1. Функция возрастает.

Если функция возрастает, но наклон касательной, проведенной в любой точке промежутка возрастания будет вправо, значит, ее коэффициент наклона положительный (k > 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.

$Функция\ возрастает\ \Rightarrow f^{'}\left( x_{0} \right) > 0$

2. Функция убывает.

Если функция убывает, но наклон касательной, проведенной в любой точке промежутка возрастания будет влево, значит, ее коэффициент наклона отрицательный (k < 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же отрицательна.

$Функция\ убывает\ \Rightarrow f^{'}\left( x_{0} \right) < 0$

3. Экстремум.

Точки экстремума, отличаются тем, что в них функция находится в пиковом значении, она и не возрастает, и не убывает. Если провести касательную в точке экстремума, то она будет строго горизонтальна, то есть ее наклон равен 0. А значит, и производная равна 0 (из соотношения между значением производной и коэффициентом наклона касательной выше).

$Точка\ экстремума\ \Rightarrow f^{'}\left( x_{0} \right) = 0$

Максимум.

До него функция возрастает, после него убывает. В максимуме производная сменяет свой знак с плюса на минус.

$Максимум:\ f^{'}\left( x_{0} \right)\ + \ \Rightarrow \ -$

Минимум.

До него функция убывает, после него возрастает. В минимуме производная сменяет свой знак с минуса на плюс.

$Максимум:\ f^{'}\left( x_{0} \right) - \ \Rightarrow \ +$

Отсюда можно вывести общий порядок действий при анализе функций:

Находим производную от функции.

Находим точки экстремума: приравниваем производную к нулю и решаем уравнение.

Определяем знаки производной между точками экстремума.

Если в точке знак производной меняется с плюса на минус — это максимум.

Если в точке знак производной меняется с минуса на плюс — это минимум.

Урок пройден! Продолжай изучать предмет дальше -> там интересно :)

Следующие темы

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной

Анализ функций

Взаимное расположение графиков линейной функции Графики тригонометрических функций Графическое применение производной Интеграл Квадратичная функция Координатная плоскость Кусочная функция Линейная функция Первообразная Правила дифференцирования Преобразование графиков функции Свойства функций Смысл производной Функции Функция квадратного корня Функция обратной пропорциональности Экстремумы

Неравенства

Параметр

Планиметрия

Реальная математика

Стереометрия

Уравнения

Формулы и выражения

Числа и действия с ними

Содержание