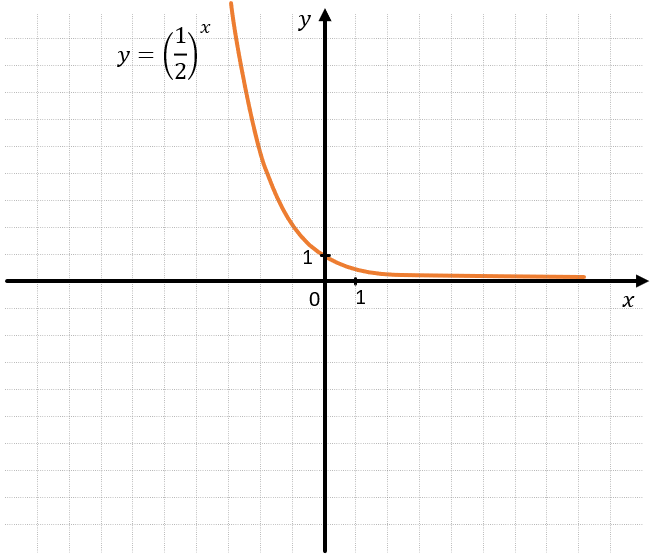Показательные выражения и свойства показательной функции
Показательные выражения и свойства показательной функции
СВОЙСТВА ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ:
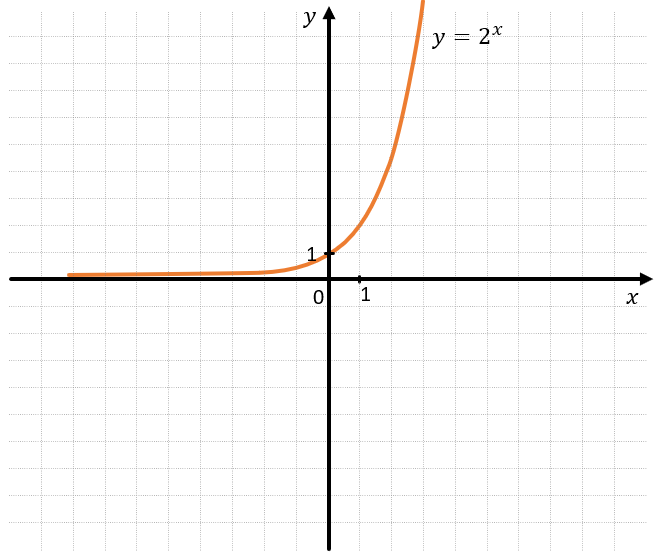
– При \(a > 1\) показательная функция монотонна возрастает:
На данном графике \(a = 2\).
– При \(0 < a < 1\ \)показательная функция монотонно убывает:
На данном графике \(a = 0,5.\)
СВОЙСТВА ГРАФИКА ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ:
| 1. Область определения: | \(D(y\mathbb{) = R}\) |
|---|---|
| 2. Область значения: | \(E(y) = (0; + \infty)\) |
| 3. Ограниченность и непрерывность: | Непрерывна, ограничена снизу |
| 4. Наибольшее и наименьшее значения | Нет |
| 5. Монотонность: | Возрастает при \(a > 1\); \(1 < a < 0.\) |
| 6. Четность: | Ни четная, ни нечетная |
| 7. Периодичность: | Не периодичная |
| 8. Пересекает ось Ох | Не пересекает ось |
| 9. Пересекает ось Оу | В точке (0; 1) |
ПОКАЗАТЕЛЬНЫЕ ВЫРАЖЕНИЯ:
Используя свойства степеней, можно преобразовывать и упрощать показательные выражения. Рассмотрим несколько примеров.
Найдите значение выражения.
\(20^{–3,9} \bullet 5^{2,9}:4^{–4,9}\)
1. Представим это выражение в виде дроби:
\(20^{–3,9} \bullet 5^{2,9}:4^{–4,9} = \frac{20^{–3,9} \bullet 5^{2,9}}{4^{–4,9}}\)
2. Представим число 20 как произведение 5 и 4:
\(\frac{20^{–3,9} \bullet 5^{2,9}}{4^{–4,9}} = \frac{{(4 \bullet 5)}^{–3,9} \bullet 5^{2,9}}{4^{–4,9}} = \frac{4^{–3,9} \bullet 5^{–3,9} \bullet 5^{2,9}}{4^{–4,9}}\)
3. По свойствам степеней объединим множители с одинаковыми основаниями:
\({\frac{4^{–3,9} \bullet 5^{–3,9} \bullet 5^{2,9}}{4^{–4,9}} = 4}^{–3,9 + 4,9} \bullet 5^{–3,9 + 2,9} = 4^{1} \bullet 5^{–1} = \frac{4}{5} = 0,8\)
Ответ: 0,8
Найдите значение выражения.
\(\frac{{(5^{\frac{3}{5}} \bullet 7^{\frac{2}{3}})}^{15}}{35^{9}}\)
1. Раскроем скобки в числителе и сократим получившиеся степени:
\(\ \frac{{(5^{\frac{3}{5}} \bullet 7^{\frac{2}{3}})}^{15}}{35^{9}} = \frac{5^{\frac{45}{5}} \bullet 7^{\frac{30}{3}}}{35^{9}} = \frac{5^{9} \bullet 7^{10}}{35^{9}}\)
2. Представим знаменатель как произведение 5 и 7:
\(\frac{5^{9} \bullet 7^{10}}{35^{9}} = \frac{5^{9} \bullet 7^{10}}{{(5 \bullet 7)}^{9}} = \frac{5^{9} \bullet 7^{10}}{5^{9} \bullet 7^{9}}\)
3. Сократим дробь:
\(\frac{5^{9} \bullet 7^{10}}{5^{9} \bullet 7^{9}} = 7\)
Ответ: 7.
Найдите значение выражения.
\(\frac{a^{3,21} \bullet a^{7,36}}{a^{8,57}}\)
Если a = 12.
1. Для начала преобразуем выражение:
\(\frac{a^{3,21} \bullet a^{7,36}}{a^{8,57}} = a^{3,21 + 7,36\ –\ 8,57} = a^{2}\)
2. Когда буквенное выражение максимально преобразовано, можно подставить данные значения:
\(a^{2} = 12^{2} = 144\)
Ответ: 144.

Содержание