Метод координат на плоскости
Метод координат на плоскости
РАЗЛОЖЕНИЕ ВЕКТОРОВ ПО ДВУМ НЕКОЛЛИНЕАРНЫМ ВЕКТОРАМ
ЛЕММА О КОЛЛИНЕАРНЫХ ВЕКТОРАХ:
Если векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\) коллинеарны и \(\overrightarrow{a} \neq 0\), то существует такое число k, что \(\overrightarrow{b} = k\overrightarrow{a}\)
Эта лемма связана со свойствами умножения вектора на число. С помощью нее доказывается следующая теорема.
ТЕОРЕМА О РАЗЛОЖЕНИИ ВЕКОРОВ:
На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем с единственными коэффициентами разложения.
\(\overrightarrow{m} = k\overrightarrow{a} + l\overrightarrow{b}\)
где k и l – единственные подходящие коэффициенты
Например,
Рассмотрим три вектора: \(\overrightarrow{a}\), \(\overrightarrow{b}\) и \(\overrightarrow{m}\).
-
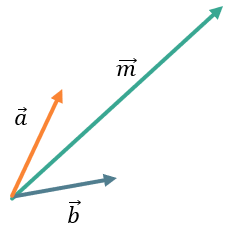
Расположим векторы так, будто вектор \(\overrightarrow{m}\) находится по правилу параллелограмма:
-
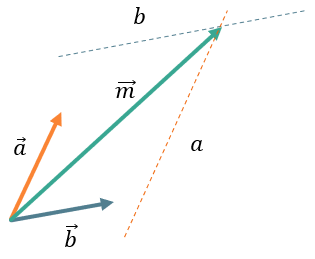
Проведем через конец вектора \(\overrightarrow{m}\) две прямые, параллельные векторам \(\overrightarrow{a}\) и \(\overrightarrow{b}\)
-
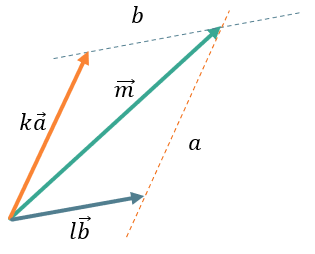
Чтобы \(\overrightarrow{m}\) являлся суммой векторов, правило параллелограмма должно выполняться верно. Тогда продлим вектора \(\overrightarrow{a}\ и\ \overrightarrow{b}\) до пересечения с прямыми b и a соответственно:
-
Действительно, сумма векторов \(k\overrightarrow{a}\) и \(l\overrightarrow{b}\) по правилу параллелограмма равна вектору \(\overrightarrow{m}\):
\(\overrightarrow{m} = k\overrightarrow{a} + l\overrightarrow{b}\)
Если бы коэффициенты k и l были равны единице, то \(\overrightarrow{m} = \overrightarrow{a} + \overrightarrow{b}\), то есть просто сумме векторов.
Таким образом можно разложить любой вектор по любым заданным неколлинеарным векторам.
КООРДИНАТЫ ВЕКТОРА
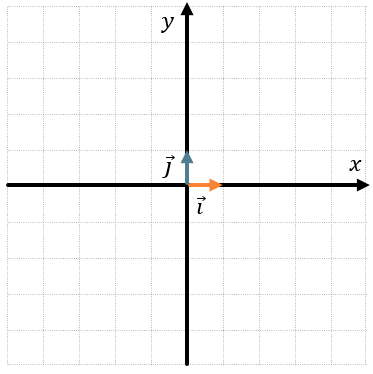
Используя разложение векторов, можно связать любой вектор с координатной плоскостью. Мы знаем, что координатная плоскость образуется двумя перпендикулярными осями, у которых есть направление и единичные отрезки. Длина и направление – две характеристики любого вектора. Рассмотрим на каждой оси единичные векторы.
Пусть вектор \(\overrightarrow{i}\) сонаправлен с осью \(Ox\), а вектор \(\overrightarrow{j}\) сонаправлен с осью \(Оy\), при этом \(\left| \overrightarrow{i} \right| = \left| \overrightarrow{j} \right| = 1\).
Получается, что длины этих векторов задают единичные отрезки, а их направления задают направления осей:
Таким образом любой вектор на координатной плоскости можно разложить по единичным векторам \(\overrightarrow{i}\) и \(\overrightarrow{j}\):
\(\overrightarrow{m} = x\overrightarrow{i} + y\overrightarrow{j}\)
где x и y – координаты вектора \(\overrightarrow{m}\)
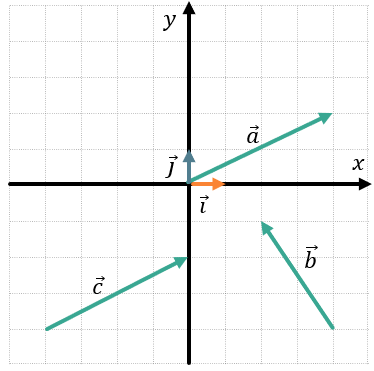
Разложите по единичным векторам и найдите координаты следующих векторов:
-
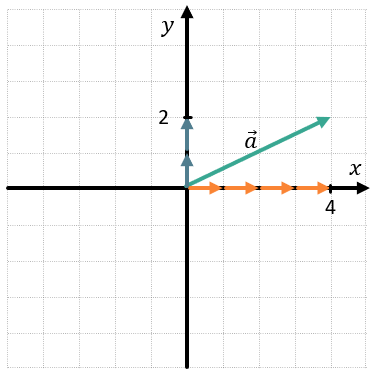
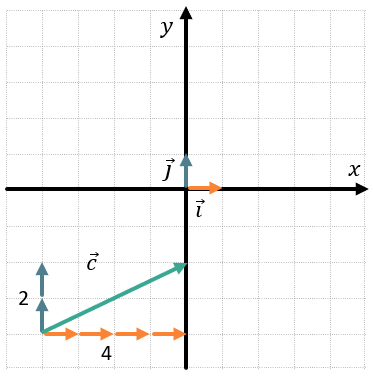
Проще всего раскладывать векторы, начало которых находится в точке \((0;0).\ \)Рассмотрим вектор \(\overrightarrow{a}\).
Для того, чтобы представить его как сумму единичных векторов, нужно посчитать, сколько отложили векторов \(\overrightarrow{i}\) и \(\overrightarrow{j}\), чтобы получить они в сумме дали вектор \(\overrightarrow{a}\). Количество отложенных векторов \(\overrightarrow{i}\) будет равнять координате x, а количество отложенных \(\overrightarrow{j}\) – координате y:
Для получения вектора \(\overrightarrow{a}\) мы сложили 4 вектора \(\overrightarrow{i}\) и 2 вектора \(\overrightarrow{j}\), то есть:
\(\overrightarrow{a} = 4\overrightarrow{i} + 2\overrightarrow{j}\)
В таком случае говорят, что вектор \(\overrightarrow{a}\) имеет координаты \(\left\{ 4;2 \right\}\) и записывают это как:
\(\overrightarrow{a}\left\{ 4;2 \right\}\)
-
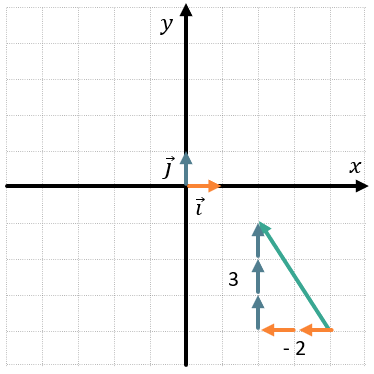
Найдем координаты вектора \(\overrightarrow{b}\) аналогично вектору \(\overrightarrow{a}\). В случае, когда начало вектора находится не в начале координат, будем отсчитывать единичные векторы от его начала:
\(\overrightarrow{b} = \ –2\overrightarrow{i} + 3\overrightarrow{j}\)
\(\overrightarrow{b}\left\{ –2;3 \right\}\)
-
Аналогично разложим вектор \(\overrightarrow{c}\) и найдем его координаты:
\(\overrightarrow{c} = 4\overrightarrow{i} + 2\overrightarrow{j}\)
\(\overrightarrow{c}\left\{ 4;2 \right\}\)
Мы видим, что координаты векторов \(\overrightarrow{a}\) и \(\overrightarrow{c}\) равны. Действительно, если мы перенесем параллельным переносом вектор \(\overrightarrow{c}\) в начало координат – точку, откуда начинается вектор \(\overrightarrow{а}\), то эти векторы совпадут. А значит векторы с одинаковыми координатами равны.
ДЕЙСТВИЯ С КООРДИНАТАМИ ВЕКТОРОВ
-
Координаты суммы векторов:
-
а) Если существуют векторы с координатами:
\(\overrightarrow{a}\left\{ x_{1};y_{1} \right\}\)
\(\overrightarrow{b}\left\{ x_{2};y_{2} \right\}\)
И есть такой вектор \(\overrightarrow{c}\), что:
\(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\)
-
б) Тогда:
\(\ \overrightarrow{a} = x_{1}\overrightarrow{i} + y_{1}\overrightarrow{j}\)
\(\overrightarrow{b} = x_{2}\overrightarrow{i} + y_{2}\overrightarrow{j}\)
\(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} = x_{1}\overrightarrow{i} + y_{1}\overrightarrow{j} + x_{2}\overrightarrow{i} + y_{2}\overrightarrow{j} = (x_{1} + x_{2})\overrightarrow{i} + (y_{1} + y_{2})\overrightarrow{j}\)
-
в) Значит координаты \(\overrightarrow{c}\) равны:
\(\overrightarrow{c}\left\{ {(x}_{1} + x_{2});{(y}_{1} + y_{2}) \right\}\)
Следовательно каждая координата суммы векторов равна сумме их соответствующих координат.
-
Координаты разности векторов:
-
а) Если существуют векторы с координатами:
\(\overrightarrow{a}\left\{ x_{1};y_{1} \right\}\)
\(\overrightarrow{b}\left\{ x_{2};y_{2} \right\}\)
И есть такой вектор \(\overrightarrow{c}\), что:
\(\overrightarrow{c} = \overrightarrow{a}\ –\ \overrightarrow{b}\)
-
б) Тогда:
\(\ \overrightarrow{a} = x_{1}\overrightarrow{i} + y_{1}\overrightarrow{j}\)
\(\overrightarrow{b} = x_{2}\overrightarrow{i} + y_{2}\overrightarrow{j}\)
\(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b} = {(x}_{1}\overrightarrow{i} + y_{1}\overrightarrow{j})\ –\ {(x}_{2}\overrightarrow{i} + y_{2}\overrightarrow{j}) = x_{1}\overrightarrow{i} + y_{1}\overrightarrow{j}\ –\ x_{2}\overrightarrow{i}\ –\ y_{2}\overrightarrow{j} = (x_{1}\ –\ x_{2})\overrightarrow{i} + (y_{1}\ –\ y_{2})\overrightarrow{j}\)
-
в) Значит координаты \(\overrightarrow{c}\) равны:
\(\overrightarrow{c}\left\{ {(x}_{1}\ –\ x_{2});{(y}_{1}\ –\ y_{2}) \right\}\)
Следовательно каждая координата разности векторов равна разности их соответствующих координат.
-
Координаты произведения вектора на число:
-
а) Если существует вектор
\(\overrightarrow{a}\left\{ x;y \right\}\) и число k
И есть вектор:
\(k\overrightarrow{a}\)
-
б) Тогда:
\(\overrightarrow{a} = x\overrightarrow{i} + y\overrightarrow{j}\)
\(k\overrightarrow{a} = k(x\overrightarrow{i} + y\overrightarrow{j}) = \text{kx}\overrightarrow{i} + ky\overrightarrow{j}\)
-
в) Значит координаты \(k\overrightarrow{a}\) равны:
\(k\overrightarrow{a}\left\{ kx;ky \right\}\)
Следовательно каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.
КООРДИНАТЫ НАЧАЛА И КОНЦА ВЕКТОРА
При нахождении координат векторов в примере №1 мы использовали визуальный метод. Также, чтобы находить координаты вектора, можно использовать координаты его начала и конца.
Координаты каждого вектора равны \({((x}_{1}\ –\ x_{2});{(y}_{1}\ –\ y_{2})\)), где начало вектора имеет координаты \((x_{1};y_{1})\), а конец координаты \((x_{2};y_{2})\).
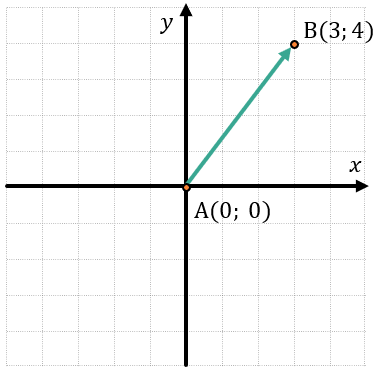
Найдите координаты вектора \(\overrightarrow{\text{AB}}\), если известны координаты точек А(0; 0) В(3; 4).
-
Для начала используем визуализацию, чтобы понять, где находится наш вектор:
-
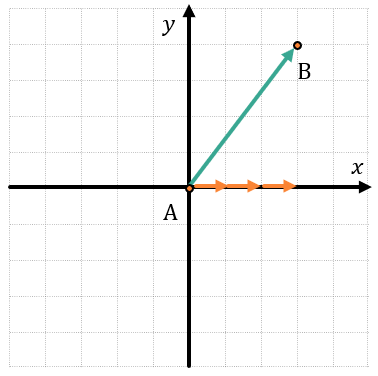
Чтобы найти координату x данного вектора, посмотрим, сколько единичных векторов \(\overrightarrow{i}\) «прошел вектор» от точки А до точки В:
Получается, что мы нашли разность между координатами x конечной и начальной точки вектора.
-
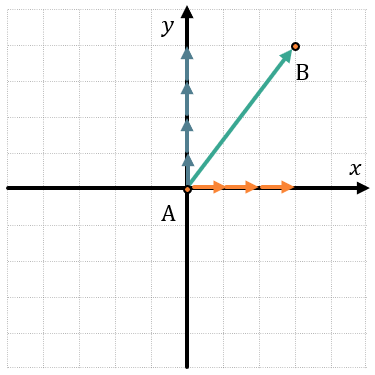
Аналогично найдем и координату y:
Она также равна разнице координат y конца и начала вектора.
-
Получается, координаты вектора \(\overrightarrow{\text{AB}}\) равны:
\(\overrightarrow{\text{AB}}\left\{ (3\ –\ 0);(4\ –\ 0) \right\}\)
\(\overrightarrow{\text{AB}}\left\{ 3;4 \right\}\)
ФОРМУЛЫ, СВЯЗАННЫЕ С ВЕКТОРАМИ
-
Координаты середины отрезка:
\(x = \frac{x_{1} + x_{2}}{2}\ и\ y = \frac{y_{1} + y_{2}}{2}\)
где \((x_{1};y_{1})\) – координаты начала отрезка,
\((x;y)\ \)– координаты середины отрезка.
-
Длина вектора:
\(\left| \overrightarrow{a} \right| = \sqrt{x^{2} + y^{2}}\)
где \((x;y)\ \)– координаты вектора \(\overrightarrow{a}\)
-
Расстояние между двумя точками:
\(\left| \overrightarrow{\text{AB}} \right| = \sqrt{{(x_{2}\ –\ x_{1})}^{2} + {(y_{2}\ –\ y_{1})}^{2}}\)
где \((x_{1};y_{1})\) – координаты точки А,
УРАВНЕНИЯ ПРЯМОЙ И ОКРУЖНОСТИ
Используя координатной метод можно вывести уравнения, которые задают расположение прямой и окружности на координатной плоскости.
Уравнением прямой является уравнение первой степени:
\(ax + by + c = 0\)
где a, b и c – некоторые числа, а x и y – координаты на координатной плоскости
Уравнением окружности радиуса r с центром в точке (x0; y0) имеет вид:
\({(x\ –\ x_{0})}^{2} + {(y\ –\ y_{0})}^{2} = r^{2}\)
Частным случаем является уравнение окружности с радиусом r и центром в начале координат:
\(\text{x\ }^{2} + \text{y\ }^{2} = r^{2}\)

Содержание