Текстовые задачи на движение по прямой
Насколько ты готов к ОГЭ?
Проверь себя и разбери результаты с экспертом
пройти тест

Текстовые задачи на движение по прямой
\(S = \vartheta t\)
где \(S\) – расстояние, \(\vartheta\) – скорость, \(t\) – время.
Через эту формулу можно выражать скорость и время:
\(\ \vartheta = \frac{S}{t}\)
\(t = \frac{S}{\ \vartheta}\)
Особенность движения по прямой заключается в том, что два объекта могут двигаться в одном направлении, а могут двигаться в разных направления (как разъезжаясь друг от друга, так и двигаясь навстречу).
ДВИЖЕНИЕ В РАЗНЫЕ СТОРОНЫ
В таком случае не важно, двигаются ли объекты друг к другу или расходятся друг от друга, важно, что они идут в разные стороны. Результат остается такой же.
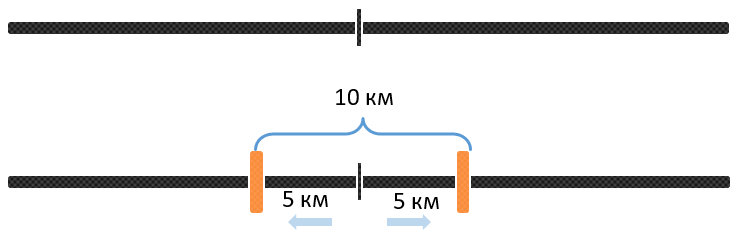
Рассмотрим ситуацию, когда два человека находятся в одной точке и начинают удаляться друг от друга, при этом скорость каждого составляется 5 км\ч. Тогда через один час каждый из них пройдет по 5 км. Значит через один час между ними станет 5 км + 5 км = 10 км:
Еще через час они отдалятся еще на 10 км. То есть через два часа расстояние между ними станет равно 20 км:
То есть при движении в разные стороны общая скорость отдаления объектов друг от друга равна сумме их скоростей. В данном случае общая скорость равна 10 км\ч:
\(\vartheta_{общ} = \vartheta_{1} + \vartheta_{2} = 5\ км\backslash ч + 5\ км\backslash ч = 10\ км\backslash ч\)
Таким образом, если нам нужно посчитать, какое расстояние будет между этими объектами через определенное время, нам нужно перемножить их общую скорость и время отдаления.
\(S = \ \vartheta_{общ}t\)
где \(\text{S\ }\)– расстояние между объектами, \(t\) – время, за которое они отдаляются, \(\vartheta_{общ} = \vartheta_{1} + \vartheta_{2}\)
Например, через 3 часа расстояние между этими объектами будет равно:
\(S = 10\ км\backslash ч \bullet 3\ ч = 30\ км\)
То же самое происходит со средней скоростью, когда два объекта находятся на определенном расстоянии и начинают сближаться.
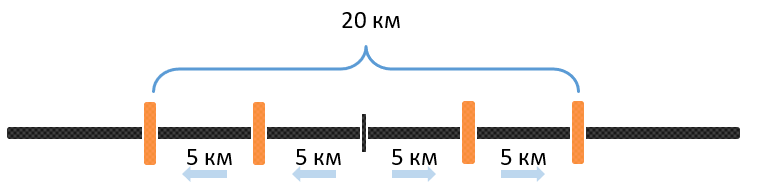
Два человека находятся на расстоянии 16 км и начинают идти навстречу друг другу. Скорость первого человека равна 3 км\ч, а второго – 5 км\ч. Через сколько часов они встретятся?
-
Рассмотрим, какова их скорость сближения. Для этого посмотрим, на сколько измениться расстояние между ними за один час:
Получается, что расстояние между двумя людьми уменьшилось за час на 3 + 5 = 8 км\ч, то есть на сумму их скоростей. Так мы убедились, что общая скорость расхождения и сближения объектов равна сумме их скоростей.
-
Тогда эти люди встретятся, когда общей скоростью пройдут расстояние в 16 км, т. е.:
\(S = t \bullet \vartheta_{общ}\)
\(16\ км = t \bullet 8\ км\backslash ч\)
\(t = 16\ км : 8\ км\backslash ч = 2\ ч\)
Ответ: 2.
ДВИЖЕНИЕ В ОДНУ СТОРОНУ
Если два человека начинают идти из одной точки в одну сторону с разной скорость, то тот, кто идет медленнее начнет отставать от того, кто идет быстрее. Со временем расстояние между ними будет становиться все больше. Каждый час оно будет расти на разность скоростей людей. Эта разность скоростей будет их общей скоростью.
\(\vartheta_{общ} = \vartheta_{2}\ –\vartheta_{1}\)
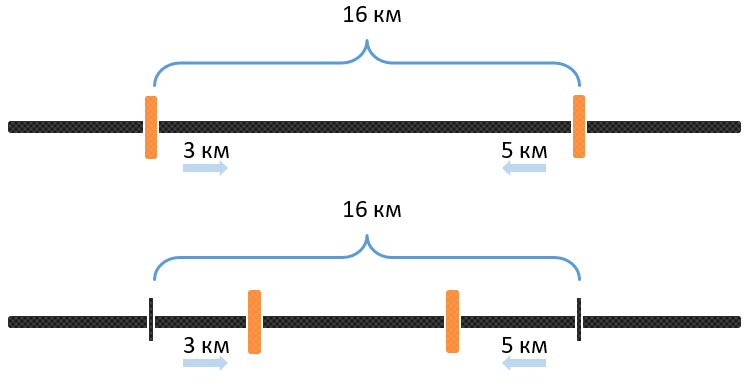
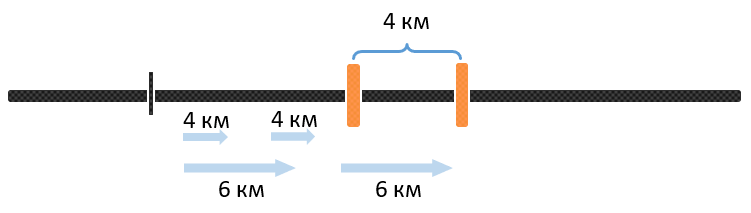
Например, два человека идут из одной точки в одном направлении. Скорость первого равна 4 км\ч, а скорость второго равна 6 км\ч. То есть быстрый пешеход пройдет 6 км, а медленный 4. Значит между ними останется 2 км:
Еще через час расстояние между ними увеличится еще на 2 км:
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
-
Составим таблицу. Обозначим за \(x\) искомую величину – скорость велосипедиста, тогда скорость автомобилиста равна \(x + 40\):
-
При этом расстояние, которое они проезжают, одинаковое. Оно равно расстоянию между городами А и В, т. е. 75 км:
-
Тогда выразим время автомобилиста и велосипедиста зная их скорость и расстояние:
-
При этом из условия задачи известно, что время, затраченное на этот путь автомобилистом, на 6 часов меньше, чем время велосипедиста. Составим и решим уравнение:
\(\frac{75}{x + 40} + 6 = \frac{75}{x}\)
-
Приведем все к общему знаменателю, в данном случае \((x + 40)x\). Перенесем се слагаемые в одну сторону и раскроем скобки:
\(\frac{75x}{\left( x + 40 \right)x} + \frac{6\left( x + 40 \right)x}{\left( x + 40 \right)x} = \frac{75\left( x + 40 \right)}{x\left( x + 40 \right)}\)
\(\frac{75x + 6\left( x + 40 \right)x\ –75\left( x + 40 \right)}{\left( x + 40 \right)x} = 0\)
\(\frac{75x + 6x^{2} + 240x\ –\ 75x\ –3000}{\left( x + 40 \right)x} = 0\)
-
Дробь равна нулю, когда числитель равен нулю, а знаменатель - нет, т. е. \(x \neq \ –40\) и \(x \neq 0\), тогда:
\(75x + 6x^{2} + 240x\ –75x\ –3000 = 0\)
\(6x^{2} + 240x\ –3000 = 0\)
\(x^{2} + 40x\ –500 = 0\)
-
По т. Виета:
\({x_{1} + x_{2} = \ –40 }{x_{1}x_{2} = \ –500}\)
Тогда:
\(\left. \ \frac{x_{1} = \ –50}{x_{2} = 10} \right\rbrack\)
-
Проверим корни на адекватность. Мы принимали за \(x\) скорость велосипедиста, но скорость не может быть отрицательной, значит ответом будет являться только корень \(x = 10\). Запишем ответ.
Ответ: 10.

Содержание