Преобразование графиков функции
Насколько ты готов к ОГЭ?
Проверь себя и разбери результаты с экспертом
пройти тест

Преобразование графиков функции
Графики функций зачастую имеют не стандартный вид. Помимо привычных простых функций, таких как \(y = x^{2}\ или\ y = \frac{1}{x}\) могут встречаться на первый взгляд более сложные функции, например, \(y = {(3x\ –1)}^{2}\) или \(y = \left| \frac{1}{x} \right|\). Чтобы построить такие графики, нужно соблюдать ряд правил преобразования функций. Каждая «сложная» функция состоит из набора таких преобразований.
ОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ:
ИЗМЕНЕНИЕ АРГУМЕНТА
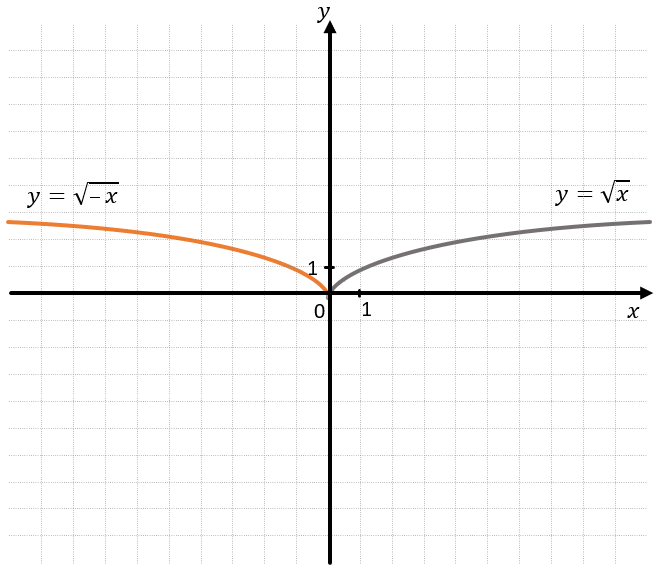
Если у мы знаем функцию f(x) и нам нужно построить функцию f(–x) (то есть заменить все иксы в функции на противоположные), тогда нужно отразить график симметрично относительно оси Оу, т.е. все ординаты останутся неизменными, а абсциссы поменяют знак.
Например:
Четная функция при таком изменении не изменяется, т.к. это следует из определения четной функции.
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
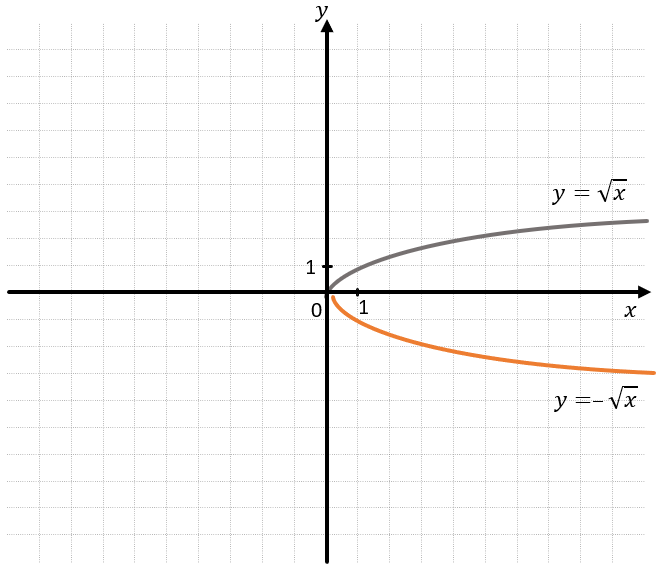
Если у мы знаем функцию f(x) и нам нужно построить функцию –f(x) (то есть заменить все значения функции на противоположные), тогда нужно отразить график симметрично относительно оси Ох, т.е. все абсциссы останутся неизменными, а ординаты поменяют знак.
Например:
СУММА ИЛИ РАЗНОСТЬ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если у мы знаем функцию \(f(x)\) и нам нужно построить функцию \(f(x\ \pm \ a)\) (то есть заменить все иксы в функции на выражения \(x\ \pm \ a\)), тогда функцию f(x) будет двигаться вдоль оси Оx.
– Если нужно построить \(f(x\ + \ a)\), то функция сдвинется влево по оси Ох на a единичных отрезков.
– Если нужно построить \(f(x\ –\ a),\) то функция сдвинется вправо по оси Ох на a единичных отрезков.
Например:
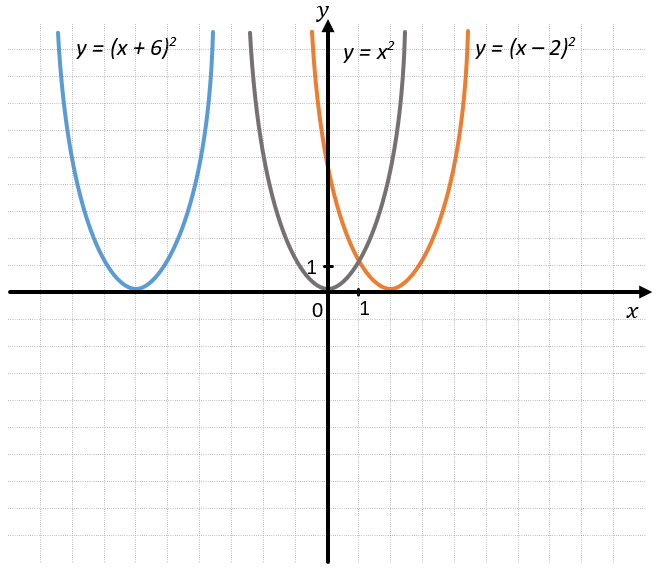
Функция \(y = {(x + 6)}^{2}\) будет находиться на 6 единичных отрезков левее, чем функций \(y = x^{2}\), а функция \(y = {(x\ –\ 2)}^{2}\) правее на 2 единичных отрезка:
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(x)\ \pm \ a\ \)(то есть прибавить к получившимся значениям функции \(\pm\) a), тогда f(x) будет двигаться по оси Оу.
– Если нужно построить \(f(x)\ + \ a\), то функция поднимется на a единичных отрезков вверх.
– Если нужно построить \(f(x)\ –\ a\), то функция опуститься на a единичных отрезков вниз.
Например:
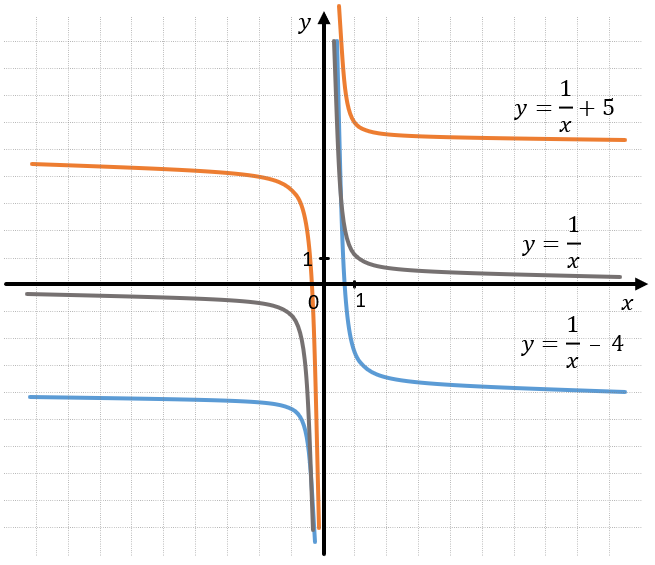
Функция \(y = \frac{1}{x} + 5\) будет выше функции \(y = \frac{1}{x}\) на 5 единичных отрезков, а функция \(\frac{1}{x}\ –\ 4\) ниже на 4 единичных отрезка:
ПРОИЗВЕДЕНИЕ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(\text{ax})\ \)(то есть заменяем все иксы на выражение ax), тогда функция \(f(x)\) будет «сжиматься» и «растягиваться» вдоль оси Ох. При этом точки пересечения графика с осью Оу не изменяться.
– Если \(a > 1\), то абсцисса каждой точки уменьшится в a раз. График «сожмется» к оси Оу
– Если \(0 < a < 1,\) то абсцисса каждой точки увеличится в a раз. График «растянется» от оси Оу.
Например:
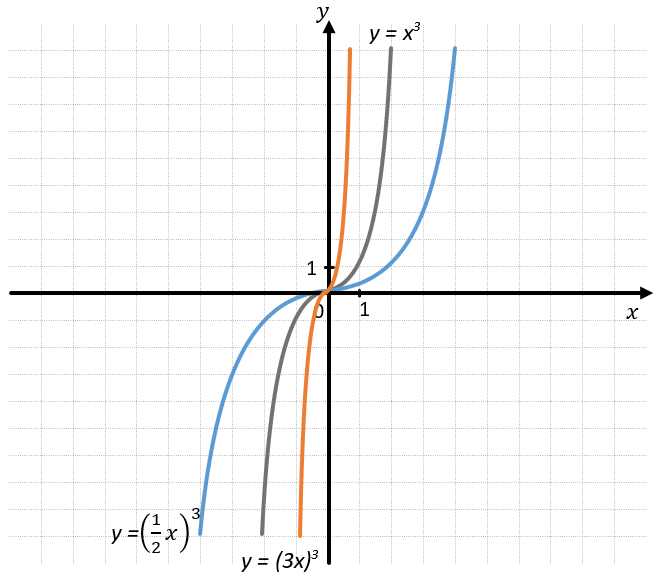
Функция \(y = {(3x)}^{3}\) будет сжата в 3 раза относительно графика функции \(y = x^{3}\) а функция \(y = {(\frac{1}{2}x)}^{3}\) будет сжата в 2 раза:
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если мы знаем функцию \(f(x),\ \)а нам нужно построить функцию \(\text{af}(x)\) (то есть умножить получившиеся значения функции на a), тогда функция \(f(x)\) будет «сжиматься» и «растягиваться» вдоль оси Оу. При этом точки пересечения графика с осью Ох не изменяться.
– Если \(a > 1,\) то ордината каждой точки уменьшится в a раз. График «сожмется» к оси Ох
– Если \(0 < a < 1\), то ордината каждой точки увеличится в a раз. График «растянется» от оси Ох.
Например:
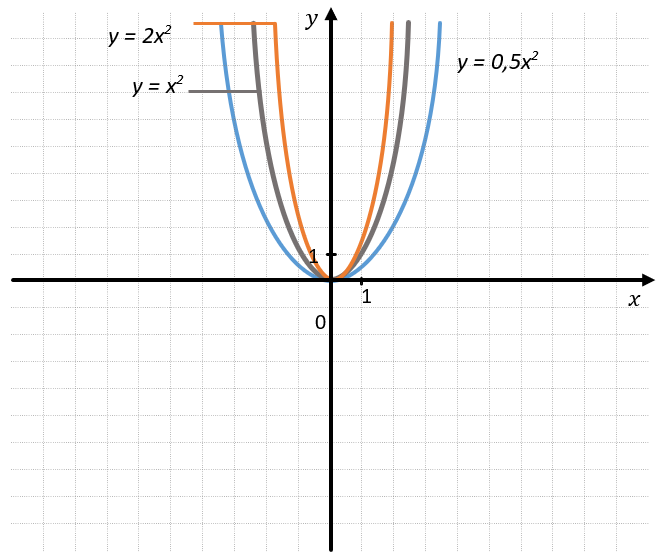
Функция \(y = 2x^{2}\) будет сжата в 2 раза относительно функции
\(y = x^{2}\), а функция \(y = \frac{1}{2}x^{2}\) растянута в 2 раза:
МОДУЛЬ:
ИЗМЕНЕНИЕ АРГУМЕНТА
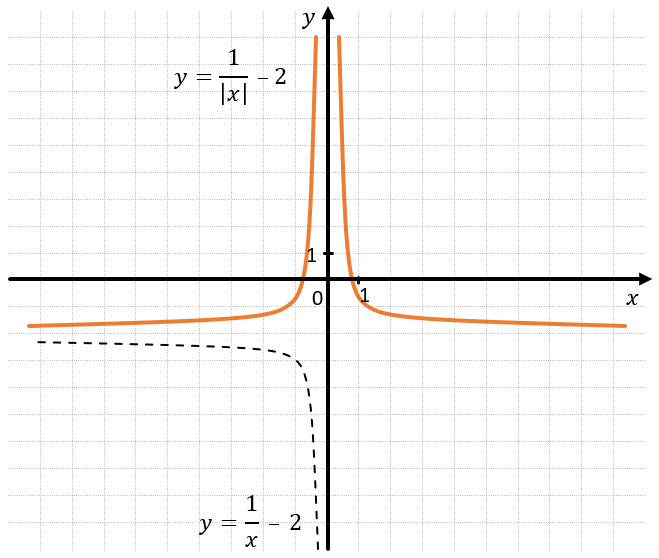
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(f(|x|)\) (то есть заменяем все иксы на модуль икс), тогда график в области с отрицательными абсциссами стирается, а график в области с положительными абсциссами отражается относительно оси Оу. Функция становится четной.
Например:
ИЗЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
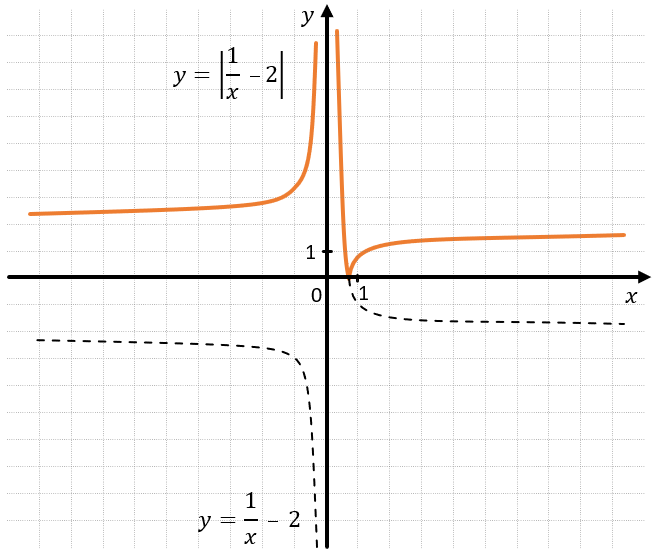
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(|f\left( x \right)|\) (то есть берем под модуль значение функции). Тогда график в области с отрицательными ординатами отражается относительно оси Ох.
Например:

Содержание