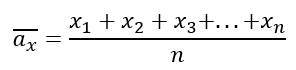Основы математической статистики
Насколько ты готов к ОГЭ?
Проверь себя и разбери результаты с экспертом
пройти тест

Основы математической статистики
Работа с основными статистическими терминами обычно осуществляется с какими-либо данными. Например, в классе взвешивали учеников. Вес каждого из них – это данные взвешивания. Для удобства такие данные выписывают в ряд, перечисляя все полученные результаты. Он будет называться числовым рядом.
Именно числовой ряд и анализируют, используя статистические термины и методы.
РАЗМАХ И ЧАСТОТА:
Такая характеристика как размах показывает, на сколько отличаются друг от друга элементы ряда.
Представим числовой ряд, состоящий из натуральных чисел:
3, 11, 18, 18, 22, 37, 37, 37, 89
В данном случае наибольшим числом является 89, а наименьшим 3.
3, 11, 18, 18, 22, 37, 37, 37, 89
Тогда размах данного ряда равен \(89–3 = 86\).
Например, частота числа 3 – 1 раз. А вот число 18 встречается 2 раза.
МОДА И МЕДИАНА:
Чтобы понять, какие средние и популярные значения присутствуют в ряду, используют такие характеристики числового ряда как мода и медиана.
В данном случае это число 37. Оно встречается три раза. Чаще него ни одно другое число не встречается. Значит оно и есть мода.
3, 11, 18, 18, 22, 37, 37, 37, 89
Например, в нашем ряде это число 22.
3, 11, 18, 18, 22, 37, 37, 37, 89
Оно является медианой, потому что в этому ряду существует четыре числа меньше числа 22 и четыре числа больше 22.
Поэтому важно выстраивать элементы по порядку, чтобы сразу заметить медиану.
Если мы добавим еще одно число в наш ряд, например допишем число 15, получим 10 чисел в ряду. Тогда по середине ряда будут находиться уже два числа: 22 и 18:
3, 11, 15, 18, 18, 22, 37, 37, 37, 89
В таком случае, если в ряду находится нечетное количество элементов, его медианой будет среднее арифметическое этих элементов.
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ:
Оно находится по следующей формуле:
Эта запись означает, что чтобы найти среднее арифметическое ряда чисел, нужно сложить все его элементы и разделить на их количество.
Найдем среднее арифметическое пятого и шестого элемента нашего ряда. Оно будет являться медианой, т.к. оба эти элементы стоят в середине ряда:
3, 11, 15, 18, 18, 22, 37, 37, 37, 89
\(m = \frac{18 + 22}{2} = \frac{40}{2} = 20\)
Действительно, если заменить сумму этих элементов на сумму такого же количества средних арифметических, то эта сумма не изменится.
\(18 + 22 = 20 + 20\)
Найдем среднее арифметическое всего ряда. Для этого сложим все элементы и поделим уже на их количество:
\(\overline{a_{x}} = \frac{3 + 11 + 15 + 18 + 18 + 22 + 37 + 37 + 37 + 89}{10} = \frac{287}{10} = 28,7\)
СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ:
Оно находится по формуле:
\(\overline{g_{x}} = \sqrt[n]{x_{1}x_{2}x_{3} \bullet ... \bullet x_{n}}\)
Это значит, что чтобы найти среднее геометрическое, нужно перемножить все элементы ряда и извлечь произведение из корня, степень которого равна их количеству.
Возьмем ряд с меньшими количеством элементов:
1, 3, 3, 5, 8
Найдем его среднее геометрическое:
\(\overline{g_{x}} = \sqrt[5]{1 \bullet 3 \bullet 3 \bullet 5 \bullet 8} = \sqrt[5]{360} \approx 3,25\)
В конце года ученику важно получить хорошую оценку за четверть. У него имеются следующие оценки по математике:
4, 3, 5, 5, 4, 4, 2, 4, 5, 5, 3, 4
Полностью проанализируем его оценки, используя статистические характеристики.
1. Для начала сделаем ряд ранжированным, т.е. расставим все его элементы по порядку:
2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5
2. Определим размах ряда. Ученик получал все возможные оценки за четверть и как мы видим, наибольшей является оценка 5, а наименьшей – 2. Тогда размах равен 5 – 2 = 3.
3. Определим моду ряда. Самой часто встречающейся оценкой является оценка 4. Её частота – 5.
4. При этом частота оценки 5 ненамного меньше и равна четырем.
5. Медианой данного ряда будет являться число по середине. Всего у нас 12 элементов ряда, тогда средними значениями будут являть шестой и седьмой элементы.
2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5
Для определения медианы из двух средних значений найдем их среднее арифметическое:
\(m = \frac{4 + 4}{2} = 4\)
Из-за того, что элементы равны между собой, их среднее арифметическое будет таким же. Медиана этого ряда – 4
6. Среднее арифметическое ряда:
\(\overline{a_{x}} = \frac{2 + 3 + 3 + 4 + 4 + 4 + 4 + 4 + 5 + 5 + 5 + 5}{12} = \frac{48}{12} = 4\)
7. Среднее геометрическое ряда:
\(\overline{g_{x}} = \sqrt[12]{2 \bullet 3 \bullet 3 \bullet 4 \bullet 4 \bullet 4 \bullet 4 \bullet 4 \bullet 5 \bullet 5 \bullet 5 \bullet 5} = \sqrt[12]{11520000} \approx 3,88\)
Таким образом мы определили, что за четверть ученик получит среднее арифметическое всех оценок, то есть 4.
Чаще всего ученик получал оценку 4, и она же является медианой. При этом ученик получал за четверть всевозможные оценки, от двоек до пятерок. Среднее геометрическое всех оценок тоже близко к 4.
По-разному проанализировав успеваемость ученика, можно убедиться в точном результате его работы. Ученику можно смело ставить четверку.

Содержание