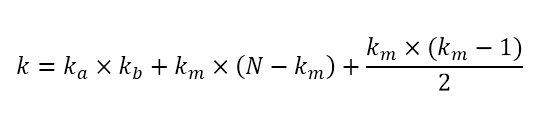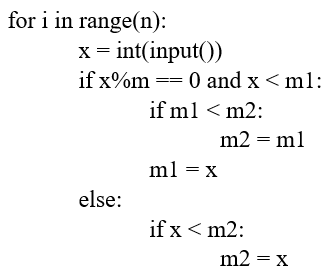Числовые последовательности

27 задание является самым сложным заданием на ЕГЭ по информатике. За его идеальное решение можно получить 2 балла. Сейчас 27 — это обновленное задание с учётом компьютерной формы проведения экзамена, так что процент решаемости именно такого вида 27-го ещё не известен, зато известно, что процент решаемости 27 задания до компьютеризации ЕГЭ составлял от 11 до 16%. Однако получить частичный балл за него, что тогда, что сейчас гораздо проще.

Для того, чтобы получить 1 балл, нужно просто написать программу, которая будет правильно работать с файлом А (файлом малого объёма). Для того, чтобы получить все 2 балла, нужно написать эффективную программу, которая так же сможет обработать файл В, который обычно намного объёмнее файла А, и его обработка неэффективной программой будет занимать слишком много времени. Поэтому следует понимать, что такое эффективная программа. Существует понятие эффективности по времени и эффективности по памяти.

Как на практике увидеть эффективность по времени? В программе отсутствуют вложенные циклы.

Хранение всех вводимых данных в массиве не способствует эффективности программы по занимаемой памяти. Именно использование массивов там, где ими можно обойтись, укажет вам на неэффективную по памяти программу.

Эффективный по всем параметрам алгоритм позволит обработать файл B и получить все 2 балла за это задание. Также этот результат позволит получить программа эффективная по времени, но не по памяти (обычнр бывает, что если программа эффективна по времени, то она оказывается эффективной и по памяти). А если правильно выполнить неэффективную программу, то можно получить лишь 1 балл.

Шаблон переборного решения

Прежде всего важно вспомнить, как правильно работать с файлом. Для этого нам предстоит его открыть. Делается это следующей конструкцией:

f = open(‘C:\Python\file_name.txt’)

где в кавычках пишется полный путь к файлу с его расширением. Однако, если файл программы и открываемый в программе файл находятся в одной папке, то можно просто написать имя файла с его расширением:

f = open(‘file_name.txt’)

Так же по окончании работы с файлом обязательно нужно его закрыть. Иначе возможны ошибки в работе как самой программы с этим файлом, так и всей системы в целом. Для того, чтобы закрыть файл, используется конструкция:

f.close()

Теперь можем переходить к стандартным алгоритмам считывания информации из файла. Сделать это можно несколькими способами:

1. Если известно, что в файле вся информация записана построчно, то можем считывать файл построчно. Делается это с помощью характерной конструкции с циклом for:

Здесь в цикле мы пробегаем по каждой строчке (line) файла, рассматривая каждую из них в отдельной итерации цикла. Для того, чтобы сохранить строчку в памяти программы, воспользуемся списком, который будем заполнять строчками line (учтём, что последний символ в строке из файла является символом переноса строки –‘\n’, поэтому будем брать срез строки файла до предпоследнего элемента line[:-1:]

2. Если наоборот про это ничего не сказано, то смело можно считывать данные сразу все и записывать их в список, как в некоторых прототипах 24 задания:

Данная конструкция будет актуальна в случае, когда нам нужно будет работать с каждым символом из файла (по аналогии с 24 заданием)

Затем после того, как считаем всю необходимую информацию из файла, можем переходить к алгоритму перебора. Перебор осуществляется конструкцией с двойным циклом for. На месте m может стоять 1, если нужно перебрать абсолютно все пары элементов в массиве. Если же нужно перебирать пары с сохранением расстояния, то на месте m окажется минимальное расстояние, указанное в условии задачи.

Внутри циклов с помощью условия if находится нужное значение. Чтобы перебрать пары, используются a[i] и a[j].

Пример 1

В файле “file.txt” содержится N целых положительных чисел по одному в каждой строке. Найдите количество пар в этой последовательности, произведение которых делится на 9.

Решение:

Пример 2

В файле “file.txt” содержится N целых положительных чисел. Найдите количество пар в этой последовательности, произведение которых делится на 9, при этом элементы в паре должны находиться на расстоянии 3 или больше (расстояние — это разность между индексами элементов последовательности).

Решение:

Так же могут встретиться задания, где в первой строке указано количество строк в файле. В этом случае отдельно считаем первую строку в отдельную переменную, которую дальше сможем использовать для прогона элементов списка в первом цикле for. То есть:

Так бы выглядело решение для примера 2, если бы в первой строке было указано количество последующих строк в файле.

Полезные алгоритмические конструкции и математические правила для решения задания 27 на 2 балла

Во всех заданиях ЕГЭ выделяются свои прототипы, и 27 задание — не исключение. Существует несколько конструкций, которые часто помогают написать максимально эффективную программу.

Буферный массив

Буферный массив — это массив, который используется при решении задач с сохранением расстояния (как в примере выше). В начале программы создается массив длиной в минимальное расстояние. Он работает как преграда, которая позволяет удерживать нужный минимум расстояния. Первые числа последовательности заносятся в массив, затем рассматриваются всегда два элемента, которые могут составить пару: первый элемент массива a[0] и вводимое на каждом проходе цикла число х. Они проверяются на нужные условия, а затем в конце цикла буферный массив перезаписывается — a[0] уходит, оставшиеся значения сдвигаются влево, а на место последнего элемента встает уже рассмотренный х.

Массив счетчиков

Массив счетчиков — это массив, в котором индексы являются указателями на какие-либо нужные значения в программе, а элементы, соответствующие индексам, в начале равны 0, а потом в них начинают накапливаться количества появлений соответствующих значений. Например, проводится голосование за 4 команды, и вам нужно посчитать, сколько за каждую команду отдали голосов. Создайте массив длиной 4, заполненный нулями. Каждый раз, когда будет встречаться определенный номер i, добавляйте 1 в соответствующий a[i-1] (здесь отнимается 1, поскольку в массиве индексация начинается с 0).

Количество пар, произведение которых кратно числу m

Если вас просят найти количество пар, произведение которых кратно m (где m = a*b, a и b — простые числа), то найдите k_a (количество чисел, которые делятся только на а), k_b (количество чисел, которые делятся только на b), k_m (количество чисел, которые делятся на m). Если количество всех чисел равно N, то количество всех нужных пар легко посчитать по следующей формуле:

Математический факт про остатки и суммы

Иногда в задаче нужно найти пару, сумма которой делится на какое-либо число m. Если остатки этих чисел в сумме дают m, то их сумма точно делится на m. Например, нужно найти пару, сумма которой кратна 7. 13 и 15 в сумме дают 28, а их остатки при делении на 7 равны 13 % 7 = 6, 15 % 7 = 1. В сумме 6 и 1 дают 7, и этим можно воспользоваться при составлении алгоритма.

Лайфхак с перезаписью минимума/максимума

Очень распространенная ошибка, которая возникает у тех, кто только начинает решать задание 27 на 2 балла, — это ошибка при поиске минимального/максимального произведения, кратного m (будем считать, что m — простое число). Если рассуждать логически, то чтобы найти такое произведение, то нужно найти в последовательности минимальное/максимальное, кратное m, и не кратное m минимальное/максимальное, а потом их перемножить. Но может оказаться, что два самых маленьких/больших числа кратны m, и тогда становится непонятно, что делать. Потому что если просто снять ограничение для некратности для второго минимума/максимума, то в обеих переменных окажется один и тот же элемент последовательности.

Рассмотрим кусок кода, в котором происходит нужная перезапись. Для определенности рассмотрим задачу поиска минимума, кратного m. В переменную m1 будет записываться минимальное, кратное m, а в переменную m2 будет записываться оставшееся минимальное (хоть кратное, хоть не кратное m).

Как можно видеть, вводимое число проверяется на кратность и минимальность. Если же оказывается, что уже записанный кратный m минимум меньше того, который есть сейчас в m2, то m2 перезапишется, и таким образом не потеряется меньшее число.

Полезные советы

• Если в начале файла дано количество чисел, то для считывания информации из файла нужно считать из первой строки количество чисел в какую-нибудь переменную (например, N) и затем, используя конструкцию for i in range(n), считать по числу из каждой строки, добавляя его в список (например, a). Если в начале файла не дано количество строк, то можно сразу после открытия файла считывать по строке и заносить значения в список данных, используя конструкцию for line in file.
• Внимательно читайте, в каком формате представлены данные в файле, это влияет на способ чтения данных из него.
• Всегда обращайте внимание на пример входных/выходных данных, часто в нем запрятаны подсказки, которые помогут вам правильно построить алгоритм на 2 балла.
• При написании программы на 2 балла всегда придумывайте для себя «опасные» случаи, в которых что-то может пойти не так, а потом вручную прогоняйте их через свою программу.
• Любая программа в 27 задании разбивается на три части: ввод, решение задачи, вывод. Тщательно проверяйте каждую из них.