Позиционные системы счисления

Системы счисления — одна из самых базовых тем в информатике. Знание систем счисления позволяет успешно решать задание№14. Также системы счисления лежат в основах логики, программирования и кодирования. В этой теме надо разбираться по порядку.

Допустим, необходимо посчитать количество цветов на поляне. Можно загибать пальцы, делать зарубки на дереве, как это делали древние люди, и так далее. Можно сделать вывод, что форма счета может быть любой, также, как и форма записи. Для способа записи чисел ввели такое понятие, как система счисления.

Существует два типа систем счисления:

Непозиционная (римская и египетская системы счисления)

Позиционная (арабская десятичная система счисления, двоичная и т.д.)

Нас будут интересовать именно позиционные системы счисления с различными основаниями. Самые популярные системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Позиционные системы счисления основаны на том, что «вес» цифры зависит от её положения — или позиции — в числе, отсюда и такое название. Для успешной подготовки к экзамену необходимо уметь переводить любое число из десятичной системы счисления в любую другую n‑ричную и из n‑ричной в десятичную. Далее приведена информация по каждому случаю.

Десятичная система счисления

Исторически сложилось, что это самая распространенная система счисления. Именно её мы используем, когда мы делаем покупки в магазине, набираем номер телефона или открываем страницу в книге. На каждой позиции может стоять только одна цифра из диапазона от 0 до 9. Основанием (то есть, количество цифр) является число 10. Это значит, что «вес» любой цифры в числе будет кратен 10 в степени, равной позиции этой цифры. При этом позиции (их называют разрядами) отсчитываются с правого конца числа, начиная с нуля.

Пример. Чтобы разобраться подробнее, возьмем число 123. Давайте «разложим» это число по разрядам. Для этого каждую цифру числа умножим на основание системы, в данном случае число 10, возведенное в степень, равную номеру разряда. Цифра 3 стоит в нулевом разряде, цифра 2 — в первом, а цифра 1 — во втором. Получается, значение равно:

1 * 10² + 2 * 10¹ + 3 * 10⁰ = 100 + 20 + 3 = 123.

При работе с разными системами счисления, чтобы избежать путаницы, справа от числа приписывают нижний индекс с основанием: 123₁₀.

Двоичная система счисления

Эта система счисления используется в вычислительной технике. Десятичную систему счисления в компьютерах не стали использовать, потому что требовалось производство устройств, способных работать в десяти состояниях, а это сильно увеличило бы цену и размер таких устройств. Двоичная же система позволяла экономить на всем.

Двоичная система счисления, как следует из названия, имеет основание 2 и использует только цифры 0 и 1.

Пример. Возьмем число 1001 — это число 9 в десятичной системе счисления. Для того, чтобы перевести число из 2-ичной в 10-ичную систему счисления, необходимо точно так же «разложить» число на разряды, т.е. каждую цифру двоичного числа умножить на основание 2, возведенное в степень, равную разряду:

1001₂ = 1 * 2³ + 0 * 2² + 0 * 2¹ + 1 * 2⁰ = 8 + 0 + 0 + 1 = 9.

Точно так же выполняется перевод из любой n-ричной системы счисления в десятичную. Для этого надо:

1. определить количество разрядов;

2. умножить каждую цифру n-ричной системы счисления на основание «n», возведенное в степень, равную разряду.

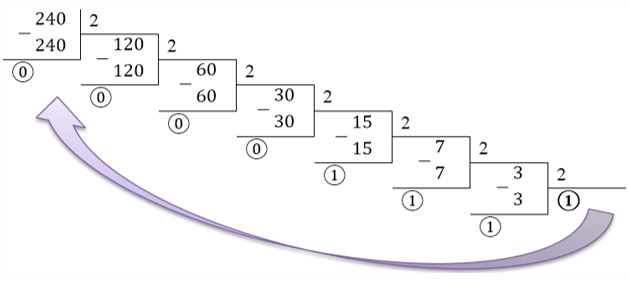
Пример. Посмотрим на то, как переводить число из десятичной системы счисления в n-ричную. Сейчас сделаем это опять на примере двоичной системы. Пусть нужно перевести число 240₁₀ в двоичную систему счисления. Для этого надо последовательно делить число 240 на 2, фиксируя получающиеся остатки (удобнее всего делать это «лесенкой»), пока не дойдем до последнего частого, которое на 2 уже не делится. Это будет первая цифра числа в двоичной системе. А остальные цифры — это получившиеся остатки, записанные в обратном порядке:

Осталось записать обведенные кружком цифры в обратном порядке, начиная с самой правой (выделена жирным). Получаем, что число 240₁₀ = 11110000₂.

Точно так же выполняется перевод из десятичной системы счисления в любую n-ричную. Для этого надо:

целую часть числа последовательно делить на основание новой системы счисления, пока не останется число или цифра, которая уже делиться не будет;

эта оставшаяся цифра будет первой цифрой нового числа. Остальные цифры — это остатки от всех делений, записанные в обратном порядке.

Восьмеричная система счисления

Имеет основание 8, использует цифры от 0 до 7.

Для того, чтобы перевести из восьмеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 8, возведенное в степень, равную разряду.

Пример. 671₈ = 6 * 8² + 7 * 8¹ + 1 * 8⁰ = 384 + 56 + 1 = 441₁₀.

Перевод из десятеричной системы счисления в восьмеричную осуществляется аналогично переводу в двоичную, только делителем в данном случае является 8.

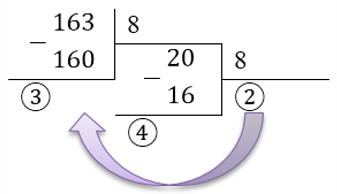
Пример. Пусть надо перевести число 163₁₀ в восьмеричную систему:

Получаем, что 163₁₀ = 243₈.

Шестнадцатеричная система счисления

Имеет основание 16, использует цифры от 0 до 9 и буква A, B, C, D, E, F, где буква А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.

Для того, чтобы перевести из шестнадцатеричной системы счисления в десятичную, нужно необходимо умножить каждую цифру восьмеричного числа на основание 16, возведенное в степень, равную разряду.

Пример. 127₁₆ = 1 * 16² + 2 * 16¹ + 7 * 16⁰ = 256 + 32 + 7 = 295₁₀.

Для того, чтобы перевести из десятичной системы счисления в шестнадцатеричную, нужно целую часть числа находить делением на основание новой.

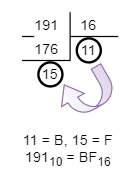
Пример. 191₁₀ переведем в шестнадцатеричную систему:

Получаем, что 191₁₀ = BF₁₆

Перевод между системами счисления, основания которых являются степенью двойки.

Для перевода чисел, записанных в восьмеричной системе в двоичный код, необходимо каждую цифру восьмеричного числа представить триадой двоичных символов.

Триады — числа, состоящие из трех цифр, грубо говоря, это перевод восьмеричных чисел от 0 до 7 в двоичную систему счисления. Тетрады состоят из четырех, и это, грубо говоря, перевод шестнадцатеричных чисел от 0 до F в двоичную систему счисления. Триады и тетрады переводятся, начиная с конца числа (т.е. с младших разрядов). Если крайние триады (тетрады) оказались неполными, они дополняются нулями. Если при переводе в двоичную систему в начале числа (слева) возникают нули, их следует отбросить (они незначащие).

Пример. 12345667₈ = 001 010 011 100 101 110 110 111₂ = 1 010 011 100 101 110 110 111₂

Таблица с триадами и тетрадами, которую надо знать наизусть.

Число	Триада	Тетрада
0	000	0000
1	001	0001
2	010	0010
3	011	0011
4	100	0100
5	101	0101
6	110	0110
7	111	0111
8		1000
9		1001
A (10)		1010
B (11)		1011
C (12)		1100
D (13)		1101
E (14)		1110
F (15)		1111

Перевод чисел с большими степенями

В задании №14 в ЕГЭ по информатике важно знать еще пару особенностей систем счисления. В десятичной системе счисления вы привыкли к тому, что 10^a (десять в степени a) равно единице с a нулями. Важно то, что во всех других позиционных системах это работает точно так же. Сформулируем соответствующее правило:

Десятичное число вида n^a в n-ричной системе счисления будет выглядеть как единица с a нулями.

Пример. Десятичное число 2⁷ в двоичной системе счисления будет выглядеть как единица и семь нулей: 10000000₂, десятичное число 5⁴ в пятеричной системе счисления будет выглядеть как единица и четыре нуля: 10000₅ и т.д.

Еще одна важная вещь касается вычитания маленьких чисел из больших круглых чисел в разных системах счисления. Если мы в десятичной системе счисления из 1000000 вычтем 1, мы получим 999999 – это никого не удивляет. Однако, в двоичной и других системах счисления понимание этого дается многим с трудом, хотя принцип абсолютно тот же самый. Сформулируем соответствующее правило:

Если необходимо из числа 1000…000_n+1, содержащего единицу и a нулей, вычесть 1_n+1, то результат будет nnn…nnn_n₊₁, где количество цифр n будет равно a.

Пример. 10000₆ – 1₆ = 5555₆, 10000000₃ – 1₃ = 2222222₃.

В форматных заданиях №16 часто встречаются прототипы, где нужно складывать и вычитать десятичные числа с большими показателями. Давайте посчитаем количество «шестерок» в выражении 7²⁵ – 7³, где числа записали в семеричной системе счисления. При переводе чисел получим, что 7²⁵ = 1000…000₇ (25 нулей), 7³ = 1000₇. Запишем решение через столбик:

Видим, что младшие 3 разряда остаются нулями, остальные разряды превращаются в шестерки. Заметим, что в получившемся числе 25 разрядов, 3 из которых – это нули, а оставшиеся 22 разряда – шестерки. Таким образом, ответом является 22.

Отметим, что мы искали количество цифр, имеющих максимальное значение в данной системе счисления. Можно заметить, что мы взяли 25 - показатель старшей степени, и вычли из него 3 - показатель младшей степени, и получили верный ответ. Такое правило работает с любым выражением, где числа имеют одинаковое основание. Сформулируем соответствующее правило:

Если необходимо десятичное число, имеющее вид aⁿ – a^m, перевести в a–ричную систему счисления, то количество цифр (a-1) будет равно разности показателей, то есть n-m.

Пример. Сколько будет единиц в двоичной записи числа 2²³⁴ -2²¹⁷? Нам нужно посчитать количество максимальных цифр в двоичной записи данного выражения. Числа имеют одинаковое основание 2, поэтому воспользуемся правилом, которое мы вывели выше, то есть 234 – 217 = 17.

Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.

Позиционные системы счисления