Анализ информационных моделей

Вокруг нас очень много информации, которую необходимо запомнить. Для того, чтобы с информацией было проще работать, её структурируют и представляют в виде понятных и простых образов. Вот эти образы и называются информационными моделями. Формулы в учебнике по физике, таблицы с расписанием рейсов в аэропорту, схема эвакуации в торговом центре — это все информационные модели. По способу передачи информации модели делят на образные (это рисунки, чертежи) и знаковые (формулы, программы на языке программирования). В целом в ЕГЭ информационным моделям посвящено аж пять заданий — №1, №3, №9, №13, №18.

В экзамене в первую очередь встречаются смешанные модели. В них входят таблицы, графики, диаграммы и схемы. Среди схем самыми важными для экзамена являются графы (ориентированные и не ориентированные), деревья и блок-схемы (умение работать с последними существенно для понимания конструкций языков программирования).

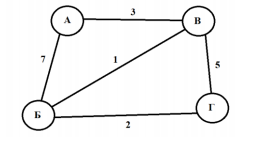
С помощью графа удобно описать, например, схему дорог с указанием расстояния между всеми пунктами. На примере ниже приведена карта (слева) и построенный по ней граф (справа):

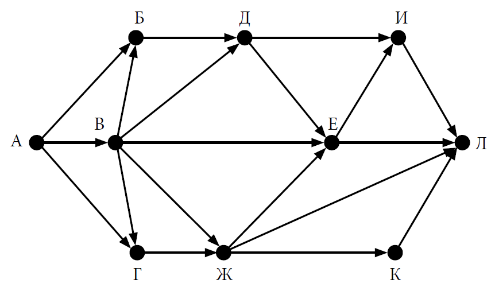
Граф, нарисованный справа, называется неориентированным. В неориентированном графе ребра не имеют направления — они показывают только связь между двумя вершинами. В противопоставление неориентированному графу существует ориентированный — такой, по которому четко видно, откуда и куда мы можем двигаться. Ниже приведен ориентированный граф из задания №13 в ЕГЭ:

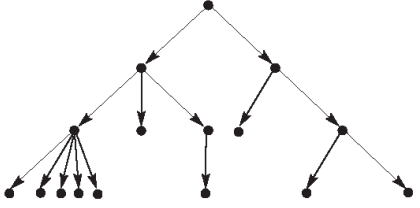
Данный вид графа имеет ветвистую структуру, поэтому и получил такое название:

Таблица — еще одна важная с точки зрения ЕГЭ информационная модель.

Например, задание №3 проверяет ваше умение находить соответствие между графами и таблицами, а также строить дерево по таблице. Последний случай особенно распространен в данном задании, поэтому его стоит разобрать отдельно. Кроме того, в экзамене особое внимание уделено электронным таблицам — важному инструменту анализа данных. Теме обработки электронных таблиц посвящено задание №9 и №18 в ЕГЭ (подробнее см. соответствующий раздел теории).

Построение дерева по таблице и алгоритм Дейкстры

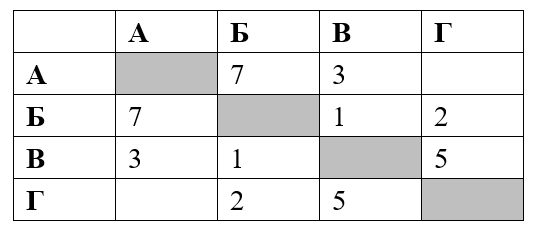
Классический прототип задания №1 выглядит следующим образом: дана таблица с населенными пунктами, в ячейках которой – расстояния между ними. Вам надо найти кратчайший путь между какими-то двумя пунктами (обычно между первым и последним) Пусть есть таблица, и необходимо найти кратчайший путь из пункта А в пункт Г:

Есть 2 способа решения данного задания:

1) Построить граф по заданной таблице.

2) Применить алгоритм Дейкстры, который назван в честь голландского ученого в области информатики и информационных технологий.

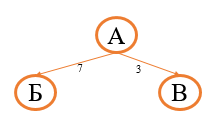
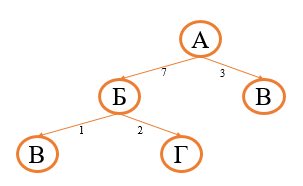
Начнем с первого способа. Нам необходимо построить граф, соответствующий заданной таблице. Из всех видов графов для этой задачи подойдет дерево, его мы и будем строить. Из вершины А можно проехать в вершину Б и В (длины путей соответственно 7 и 3):

Из вершины Б можно проехать в вершины В и Г (длины путей соответственно 1 и 2):

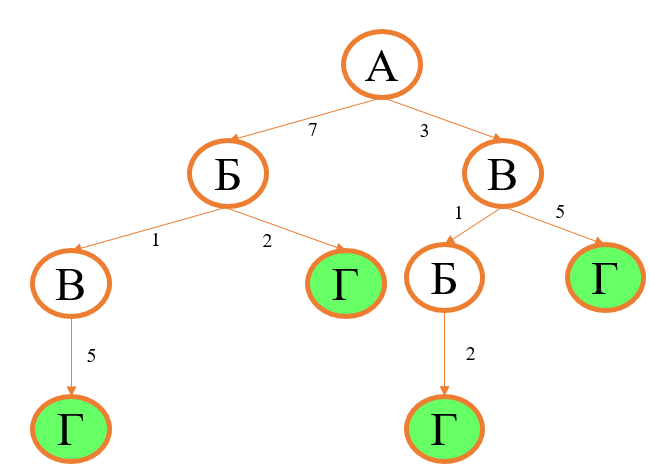
Новые маршруты из В – в Г (длина пути 5) и т.д.:

Получаем, что кратчайший путь – это путь А-В-Б-Г, длина которого равна 6.

Рассмотрим алгоритм Дейкстры для решения этой же задачи. Суть алгоритма заключается в том, что возле каждой вершины будут стоять временные метки, которые будут обновляться в соответствии с найденными минимальными путями. Метка возле финального пункта назначения будет ответом на задачу.

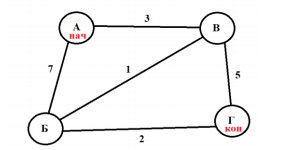
Первое, и самое важное, - правильно нарисовать граф.

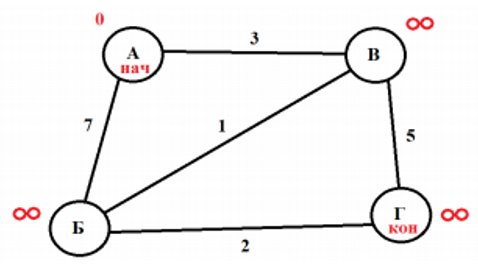
Отметим начало и конец.

Около каждой из вершины, кроме начальной оставим временную метку – бесконечности, а около начальной вершины – метку 0, ведь нахождение кратчайшего пути начинаем с нее. Именно с временными метками мы будем сравнивать, является ли маршрут минимальным или нет.

Начинаем со стартовой вершины. Рассматриваем возможные передвижения из нее. То есть в

вершину В и вершину Б. Рассчитываем новую временную вершину следующим образом:

складываем временную метку у исходной вершины с весом ребра, проходящего к необходимой

вершине:

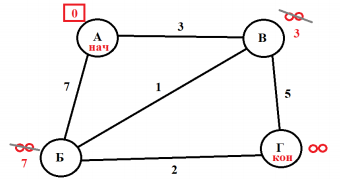
Для вершины В: 0 + 3 = 3

Для вершины Б: 0 + 7 = 7

Далее определяем, является ли новая метка, меньше чем предыдущая?

Для вершины В: 3 меньше чем бесконечность, поэтому бесконечность зачеркиваем и пишем

новую временную метку – 3.

Для вершины Б: аналогично. Зачеркиваем предыдущую временную метку, и ставим новую – 7.

Так как мы рассмотрели вершину А, ее временная метка становится постоянной и не может быть

изменена.

Таким образом, мы должны рассмотреть все вершины. Причем нельзя рассматривать уже

пройденные вершины. Только те, что имеют врЕменные метки.

Для того, чтобы определить, какую следующую вершину необходимо рассматривать, пользуемся

правилом: «У кого меньше значение временной метки, тот наш герой!».

В нашем случае этот герой вершина В!

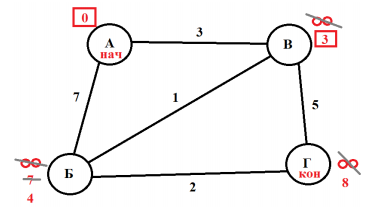
В–Б: 3 + 1 = 4. Четверка меньше семи, поэтому зачеркиваем 7, и ставим новую метку – 4.

В–Г: 3 + 5 = 8. Восемь меньше бесконечности, поэтому зачеркиваем бесконечность, и ставим

новую метку – 8.

Делаем временную метку 3 у вершины В постоянной, тем самым показывая, что эта вершина

рассмотрена.

Следующая вершина – Б.

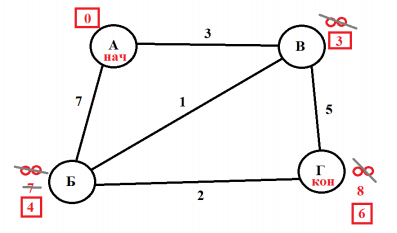
Б–Г: 4 + 2 = 6. Шесть меньше чем 8, поэтому зачеркиваем 8, и ставим новую временную метку – 6.

Временная метка у Б теперь постоянная.

Остается последняя вершина Г, которая является конечной. И ее временная метка становится

постоянной и является ответом на нашу задачу. Кратчайший путь между вершинами А и Г – 6.

Ответ сошелся с предыдущим способом!

Теперь вы знаете два возможных способа найти кратчайший путь в графе!

Стоит отметить, что с помощью обоих алгоритмов можно находить как самый короткий, так и самый длинный путь. При построении дерева достаточно просто выбрать ветку с максимальным итоговым значением. При применении алгоритма Дейкстры, при перезаписи временной метки вершины, вместо выбора наименьшего значения, мы будем выбирать наибольшее.