Теория игр

Теория игр – это раздел прикладной математики, изучающий оптимальные стратегии в играх. Под игрой в теории игр понимается процесс, в котором есть несколько противоборствующих сторон, ведущих борьбу за свои интересы. В игре должны быть правила – они определяют, как может действовать игрок в той или иной ситуации. Теория игр – достаточно серьезная вещь, которая применяется во многих сферах науки. Первые ее применения касались экономики и финансов – результаты математического моделирования могли помочь принять верное экономическое решение, и, например, не остаться банкротом. С точки зрения информатики теория игр имеет огромное значение для изучения и разработки искусственного интеллекта и кибернетики, поэтому основы теории игр изучают почти на всех IT-направлениях в вузах.

В ЕГЭ по информатике теория игр представлена в заданиях №19, 20 и 21. Конечно, в экзамене никаких сложных математических выкладок не будет, но некоторые базовые понятия надо знать и понимать очень хорошо.

Стратегия игрока – это определенная модель поведения игрока, тот набор ходов, который он выбрал использовать. Стратегия может быть выигрышной (приводить к победе) и проигрышной.

Множество всех партий, которые могут получиться при данной стратегии, представляется в виде дерева, это дерево называется деревом всех партий для заданной стратегии. В узлах дерева – позиции игры; на рёбрах – ходы, которые переводят одну позицию в другую; корень дерева – начальная позиция игры. Дерево всех партий для данной стратегии может быть также описано с помощью рисунка или таблицы.

Выигрышная стратегия – это такая стратегия, которая позволяет выигрывать при любых ходах другого игрока. Представим, что есть Игрок 1 и Игрок 2, при этом у Игрока 1 есть выигрышная стратегия. Это значит, что, как бы ни ходил Игрок 2, выбранные ходы Игрока 1 всегда приведут его к победе. Понятно, что выигрышная стратегия есть не всегда – ее наличие зависит от условий и позиции в игре. Кроме того, выигрышная стратегия в каждом конкретном случае может быть только у одного игрока! Если Игрок 1 имеет выигрышную стратегию, то, если он будет ее придерживаться, Игрок 2 никогда не сможет победить.

Теория игр в ЕГЭ

В экзамене все прототипы задания на теорию игр имеют похожий формат. Вам даны правила некоторой игры, в которую играют два друга (они могут, например, собирать кучу из камней, закидывая в нее по очереди строго определенное количество камней). На самом деле игроки в подобных играх всегда действуют по определенному алгоритму, и ваша задача – распознать этот алгоритм, построить по нему дерево для визуализации, чтобы получить верный ответ. Ранее данный прототип находился во второй части экзамена и проверялся экспертами, поэтому построение дерева являлось неотъемлемой частью решения, и экзаменуемым приходилось тратить значительную часть времени для прорисовки дерева в бланк ответов. С 2021 года решения по теории игр не будут оцениваться экспертом, но без построения дерева все равно невозможно обойтись, так как именно при грамотной визуализации условий заданий и алгоритма возможно получить правильный ответ.

Рассмотрим, как визуализировать условия задачи и ход игры с помощью дерева на примере следующей задачи.

Пример задания

Два игрока, Паша и Валя, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в кучу один камень или увеличить количество камней в куче в два раза. Например, имея кучу из 15 камней, за один ход можно получить кучу из 16 или 30 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.

Игра завершается в тот момент, когда количество камней в куче становится не менее 32.

В начальный момент в куче было S камней, 1 ≤ S ≤ 31. У кого из игроков есть выигрышная стратегия при S = 14? Опишите соответствующие выигрышные стратегии.

Пример построения дерева

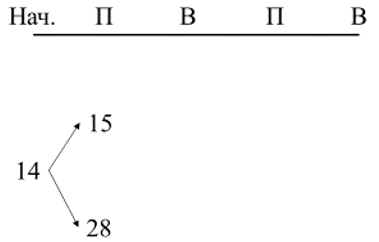
Начнем строить дерево. Начальное положение – точка 14 (количество камней в куче в начале игры). Первым ходит Паша, он может получить количество камней в куче 15 или 28:

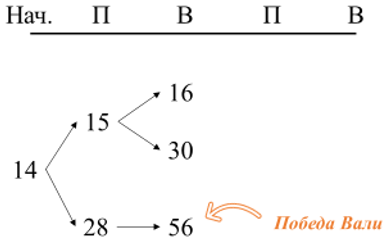
Какие ходы может сделать Валя в этих позициях? Из 28 Валя может сразу получить 56 и победить. Также из 15 Валя может сделать кучу в 16 и в 30 камней:

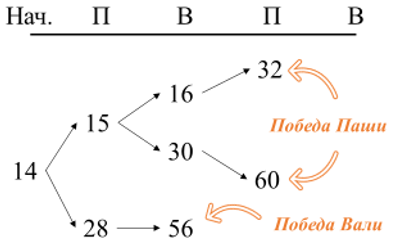
Из кучи в 16 камней и в 30 камней у Паши есть победный ход – достаточно в каждом из этих случаев удвоить количество камней в куче, чтобы выиграть:

Мы построили дерево, содержащее победные ходы для обоих игроков. Теперь давайте его проанализируем. Может ли какой-то игрок ходить так, чтобы другой игрок не имел возможности победить? При анализе дерева игры главное – внимательность. Посмотрите на первый ход Паши: если Паша увеличивает количество камней в куче в два раза и получает 28, то сразу следующим ходом выигрывает Валя. Тут важно понимать, что Валя тоже не дурак, она (или он?) не будет использовать невыгодные для себя ходы и получать из кучи 28 камней кучу в 29 камней, ведь можно сразу победить, удвоив количество камней в куче и получив 56. Поэтому ход в 28 камней для Паши является ошибочным – он «дарит» победу Вале, позволяя ей выиграть следующим ходом сразу. Теперь давайте посмотрим на ветку дерева, в которой Паша первым ходом получает 15 камней. При любых ходах Вали – 16 или 30 камней в куче – Паша побеждает следующим своим ходом (из 16 – получив 32, из 30 – получив 60 камней). Буквально, какой бы ход не был сделан Валей, Паша все равно побеждает. Но ему для этого нужно первым ходом получить кучу в 15 камней. Это и есть выигрышная стратегия для Паши. Давайте построим дерево для данной выигрышной стратегии:

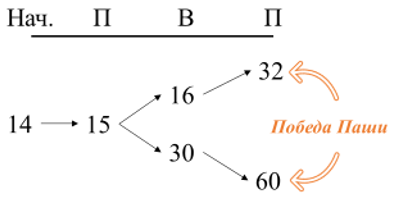
Мы описали дерево всех партий для данной стратегии – обратите внимание, оно не содержит ходов, не относящихся к выигрышной стратегии Паши (например, нет ветки, в которой Паша первым ходом получает 28 камней), зато оно обязано содержать ВСЕ ХОДЫ проигрывающего игрока (мы должны показать, что выигрывающий игрок побеждает при ЛЮБЫХ ходах противника, иначе его стратегию нельзя будет назвать выигрышной по определению).

В каждом случае анализировать дерево игры и определять выигрывающего игрока нужно отдельно. В данных условиях (при исходном количестве камней S = 14) выигрышная стратегия была у Паши. При другом S выигрышная стратегия могла быть у Вали. Для тренировки можете попробовать найти такие значения. Условия игры оставьте теми же.

Таким образом, мы определили, что при значении S = 14 у Паши есть выигрышная стратегия, значит эта позиция является заведомо выигрышной, так как игрок, оказавшийся в ней, побеждает при любом ходе противника. Для Вали сложилась обратная ситуация – после хода Пети, он попал в S = 15, и мы рассмотрели, что как бы не сходил Валя, он все равно проиграет. Можно сказать, что S = 15 является заведомо проигрышной позицией, так как игрок, оказавшийся в ней, в любом случае проигрывает.