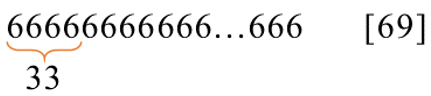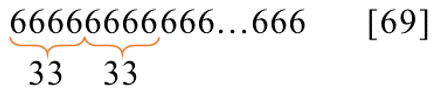Исполнитель

Исполнитель в информатике – это человек, группа людей, животное, машина или другой объект (да вообще что угодно), который может понимать и выполнять некоторые формальные команды. Задания с исполнителем очень любят в ФИПИ – в экзамене эта тема встречается аж в трех заданиях – №5, №12 и №23. В каждом из номеров вы будете иметь дело с некоторым алгоритмом. В данном разделе теории речь идет про задания №5 и №12. По заданию №23 см. раздел теории к уроку «Поиск путей в алгоритме».

Алгоритм – это совокупность последовательных шагов, схема действий, приводящих к желаемому результату. Чтобы определить все возможные результаты работы алгоритма, нужно обозначить входные данные как переменные и выполнить алгоритм.

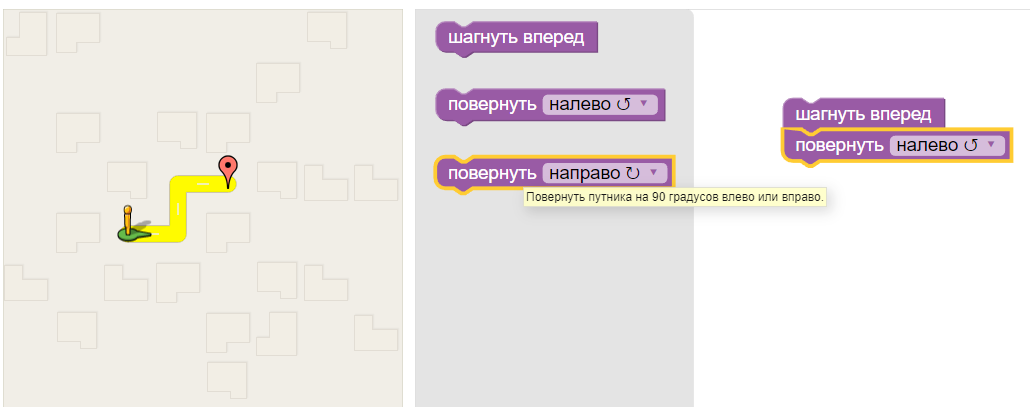
Пример. На карте внизу человеку нужно попасть в пункт, обозначенный красной меткой. Для нас этот человек играет роль исполнителя. Чтобы попасть в необходимую точку, исполнителю нужно выполнить 3 шага алгоритма: 1) шагнуть вперед; 2) повернуть налево; 3) повернуть направо.

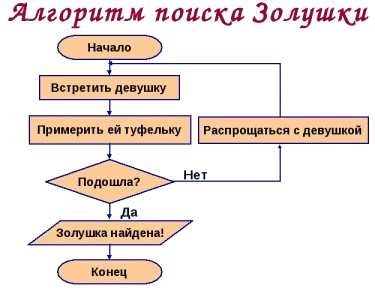
В случае, когда алгоритм содержит условия или ветвится, его удобно представлять в виде блок-схемы. Представим, что нам надо сформулировать алгоритм поиска Золушки. Недолго думая, придем к следующей блок-схеме:

Исполнитель в ЕГЭ

Несмотря на большое количество задач с исполнителем в ЕГЭ, среди них можно выделить несколько самых важных прототипов. В задании №5 могут встретиться:

1. исполнитель, выполняющий арифметические операции с числами;
2. исполнитель-робот, перемещающийся по клеточной доске;
3. исполнитель-кузнечик, перемещающийся по координатной плоскости;
4. исполнитель, выполняющий двоичные преобразования числа;
5. исполнитель, работающий с цифрами числа.

В задании №12 могут встретиться:

1. исполнитель-робот, перемещающийся по клеточной доске;
2. исполнитель, работающий с длинными цепочками цифр.
3. исполнитель-чертежник.

Самым, пожалуй, важным и наиболее актуальным прототипом задания №5 является прототип с исполнителем, выполняющим двоичные преобразования числа. А среди прототипов задания №12 таковым является прототип исполнителя, работающего с длинными цепочками цифр. Далее приведены примеры решения каждого из этих заданий.

Пример задания №5 с исполнителем, выполняющим арифметические действия.

Исполнитель КВАДРАТОР имеет только две команды, которым присвоены номера:

1. возведи в квадрат

2. прибавь 1

Выполняя команду номер 1, КВАДРАТОР возводит число на экране в квадрат, а выполняя команду номер 2, прибавляет к этому числу 1. Напишите программу, содержащую не более 4 команд, которая из числа 1 получает число 17. Укажите лишь номера команд.

Пример решения.

Команды: ХХХХ

Воспользуемся обратным ходом поиска решения данной задачи. 17 – не является квадратом числа, значит могли лишь прибавить 1. Команды: ХХХ2.

16 – является квадратом числа, значит возвели в квадрат. Команды: ХХ12.

4 – является квадратом числа, значит возвели в квадрат. Команды Х112.

2 – а мы должны были начать с 1, значит нужно было прибавить. Команды: 2112.

Ответ: 2112.

Пример задания №5 с добавлением двоичных битов.

На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом:

1. Строится двоичная запись числа N.
2. К этой записи дописываются справа ещё два разряда по следующему правилу:

- складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа).

Например, запись 11100 преобразуется в запись 111001;

- над этой записью производятся те же действия – справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает 75 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

Пример решения.

В задании идет речь про бит четности – добавочный бит справа от двоичного числа, который выбирается так, что количество единиц в числе становится четным (если до этого их было нечетное число – добавляется 1, если их и так было четное число – добавляется 0). «Остаток от деления суммы на 2» как раз и показывает, четное ли количество единиц в двоичном числе.

Чтобы выяснить, какое число, большее 75, может являться результатом работы алгоритма, надо проверять все числа, начиная со следующего – 76. Как правило, в таких заданиях надо будет проверить не более 3-4 чисел подряд, так что решаются они довольно быстро. Итак, проверяем. Для этого переводим 76 в двоичную систему. Поскольку сейчас мы проверяем РЕЗУЛЬТАТ работы алгоритма, то предполагаем, что последние два бита – это те, что были добавлены алгоритмом. Осталось выяснить, мог ли исполнитель добавить такие биты согласно правилам.

76₁₀ = 1001100₂ – не подходит (в числе до добавления битов было три единицы, значит, первым добавленным битом должна была быть единица, а здесь – 0)

77₁₀ = 1001101₂ – не подходит по той же причине

78₁₀ = 1001110₂ – подходит. Смотрите, число до выполнения алгоритма было 10011₂. В нем три единицы, значит первым битом четности добавится 1: 100111₂. Теперь в числе уже четное число единиц, значит, вторым битом четности добавится 0: 1001110₂. Нас спрашивали про число, которое МОЖЕТ ЯВЛЯТЬСЯ РЕЗУЛЬТАТОМ РАБОТЫ алгоритма, значит, нас интересует именно число 1001110₂, т.е. 78.

Ответ: 78.

P.S. В подобных заданиях также встречается другая формулировка вопроса: укажите минимальное число N, ПОСЛЕ ОБРАБОТКИ КОТОРОГО с помощью этого алгоритма получается число, большее, чем 75. В этом случае, найдя, что 78 может являться результатом работы алгоритма, нам стоило отбросить два последних бита и получить число 10011₂ = 19₁₀ – то есть то, которое было до обработки.

Пример задания №12 с цепочками цифр.

Исполнитель Редактор получает на вход строку цифр и преобразовывает её.

Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды

заменить (111, 27) преобразует строку 05111150 в строку 0527150.

Если в строке нет вхождений цепочки v, то выполнение команды

заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Какая строка получится в результате применения приведённой ниже программы к строке, состоящей из 69 идущих подряд цифр 6? В ответе запишите полученную строку.

Пример решения.

Чтобы решить такое задание, надо проанализировать, что будет происходить с цепочкой. В таком задании всегда появляется повторяющийся «шаблон» действий алгоритма, давайте его найдем. На первом этапе алгоритм найдет в числе первые 6666 и заменит на 33:

Затем найдет еще 6666 и снова заменит на 33:

Затем найдет 3333 (потому что проверка на поиск и замену 3333 стоит в программе раньше, чем на 6666) и заменит на 66:

Тройки пропадут, но в последовательности станет на шесть шестерок меньше. Вот и шаблон действий, который мы нашли – через каждые три итерации цикла из цепочки будет уходить шесть шестерок:

Чтобы понять, что останется после окончания работы алгоритма, давайте посмотрим сколько раз эти 6 шестерок смогут убраться. Для этого достаточно посчитать целую часть от деления 69 на 6. Это будет 11. Значит, вот такое шаблонное действие – три итерации, приводящие к удалению шести шестерок – произойдет ровно 11 раз. Всего в ходе этих 11-ти действий удалится 6×11 = 66 шестерок. Останется, очевидно, три: 666. Эти шестерки проигнорируются алгоритмом, т.к. он проверяет наличие четырех цифр, а осталось только три. Алгоритм остановится, ответ – 666.

Ответ: 666.

Пример задания №12 с чертежником.

Исполнитель Чертёжник перемещается на координатной плоскости, оставляя след в виде линии. Чертёжник может выполнять команду сместиться на (a, b), где a, b – целые числа. Эта команда перемещает Чертёжника из точки с координатами (x, y) в точку с координатами (x + a, y + b).

Например, если Чертёжник находится в точке с координатами (4, 2), то команда сместиться на (2, −3) переместит Чертёжника в точку (6, −1). Чертёжнику был дан для исполнения следующий алгоритм (количество повторений и величины смещения в первой из повторяемых команд неизвестны):

В результате выполнения этого алгоритма Чертёжник возвращается в исходную точку. Какое наибольшее число повторений могло быть указано в конструкции «ПОВТОРИ … РАЗ»?

Пример решения.

Введем обозначения: n – количество повторений, a – неизвестный переход по оси икс, b – по оси игрек.

Составим уравнения передвижения исполнителя по осям икс и игрек:

X: 1 + n * (a – 1) – 26 = 0 (Так как исполнитель вернулся в исходную точку).

Y: 2 + n * (b – 2) – 12 = 0

Преобразуем уравнения.

X: n * (a – 1) = 25
Y: n * (b – 2) = 10

Заметим, что нам необходимо наибольшее такое n, и при этом 25 и 10 должны делиться на n нацело. Значит, нам необходим НОД(25, 10) = 5.

Ответ: 5.