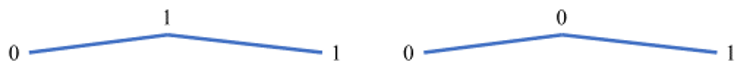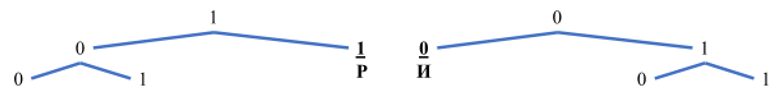Кодирование и декодирование информации
Насколько ты готов к ЕГЭ?
Проверь себя и разбери свои результаты с экспертом
пройти тест

Кодирование и декодирование информации
Кодированию и декодированию информации в ЕГЭ по информатике посвящено задание №4. Вообще кодирование информации – это процесс преобразования сигнала из формы, удобной для непосредственного использования информации, в форму, удобную для передачи, хранения или автоматической переработки. Кодирование как явление появилось очень давно. Еще древние люди пускали своим соплеменникам сигналы дымом от костра – в современном понимании это был своеобразный код. Еще старый пример кодирования – это всем знакомая азбука Морзе.
На сегодняшний день под кодированием в первую очередь понимают представление любой информации (текстовой, аудиовизуальной и т.д.) в виде последовательности двоичных цифр (двоичного кода) для хранения и передачи в компьютерных системах. Например, музыка – это набор звуков. Но хранить в компьютере набор звуков вряд ли получится. А вот хранить последовательность единиц и нулей в определенном порядке так, чтобы из них можно было получить тот самый набор звуков – запросто. На сегодняшний день существует огромное количество методов и способов кодирования любой информации. Для экзамена же вам понадобится самый простой тип кодирования – кодирование с выполнением условия Фано.
Открывателем этого кодирования является итальяно-американский ученый в области информатики Роберт Фано. Формулировка этого условия выглядит следующим образом: Никакое кодовое слово не может быть началом другого кодового слова. Такое кодирование позволяет однозначно декодировать любое сообщение слева направо. Проще всего объяснить на примере. Например, нам надо передать три символа алфавита: А, Б и В. Закодируем А как 1, Б как 10 и В как 0. Теперь передадим нашему собеседнику последовательность: 10. Когда он попытается декодировать последовательность, у него возникнет проблема: он может интерпретировать наше сообщение как АВ, а может – как Б. Так получилось, потому что выбранный нами код не удовлетворял условию Фано – код для А (1) является началом кода для Б (10). Если же мы используем кодировку, удовлетворяющую условию Фано, то такой ситуации в принципе не может произойти – двоякость декодирования будет исключена. Действительно, пускай А = 10, Б = 01, В = 11. Такой код удовлетворяет условию Фано. Поэтому, получив последовательность: 01111001110110 и декодируя ее слева направо, наш собеседник однозначно получит сообщение БВАБВБА. Примером кода, удовлетворяющего условию Фано, являются телефонные номера в традиционной телефонии. Если в сети существует номер 101, то номер 1012345 не может быть выдан: при наборе трёх цифр АТС прекращает понимать дальнейший набор и соединяет с адресатом по номеру 101 (с мобильными номерами это не работает).
Выбор наименьшего кодового слова по условию Фано
В одном из характерных прототипов задания №4 требуется определить наименьшее возможное кодовое слово для кодирования некоторой буквы. Ниже приведен пример данного задания и пример решения с помощью дерева разрядов.
Пример задания №4.
По каналу связи передаются шифрованные сообщения, содержащие только восемь букв: А, Б, Г, Е, И, М, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово | Буква | Кодовое слово | |
|---|---|---|---|---|
| А | 0101 | И | 00 | |
| Б | 1000 | М | 0100 | |
| Г | 011 | Р | 11 | |
| Е | Т | 1001 |
Укажите кратчайшее кодовое слово для буквы Е. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Пример решения.
Самый надежный способ решить такое задание – составить дерево для уже имеющихся кодов и незанятой последовательностью закодировать нужную букву. Строить дерево будем по уровням, каждый уровень – это один разряд кодового слова, начиная со старшего разряда. Любое двоичное кодовое слово можно начать либо с единицы, либо с нуля:
Далее от единицы и от нуля отдельно добавляем следующие разряды по веткам:
Посмотрите на таблицу, на буквы И и Р. Они закодированы словами 00 и 11. Значит, дальше ветки, которые начались с 00 и 11, мы продолжать не можем – иначе получится, что буквы И и Р (00 и 11) будут началом этих последующих кодовых слов, а это не удовлетворяет условию Фано. Обозначим на дереве, что эти ветки для нас завершились и станем продолжать остальные:
Нашли еще букву Г (011). Дальше эту ветку продолжать также не можем. Больше у нас нет букв, закодированных трехзначными двоичными словами. Давайте посмотрим, как закодированы остальные буквы из таблицы, кодовые слова для которых мы точно знаем. Внимательный читатель уже наверняка видит, как нужно закодировать искомую букву Е. Но все по порядку:
Отметим все оставшиеся буквы. После этого мы сможем точно определить место для буквы Е:
Смотрите, оказалось, что заняты все ветки, кроме одной – 101. В этой ветке нет никаких кодовых слов. По большому счету это означает, что искомую букву Е мы можем закодировать любой последовательностью, начинающейся с 101. Но нам нужен код с наименьшим числовым значением, то есть самый маленький из всех возможных. А это и есть сама последовательность 101, без всяких дополнительных разрядов:
Ответ: 101.

Наши социальные сети
Подписывайся!
Экономь время
на подготовке в ТГ
Забирай полезные чек-листы, памятки и лайфхаки
Подписаться →

Изучай новое
без усилий в ВК
Смотри полезные видео и вебинары, где объясняем сложное простым языком
Подписаться →

Забирай полезное в Максимум БЛОГЕ
Узнай первым лайфхаки по решению заданий предстоящего экзамена
Подписаться →

Содержание