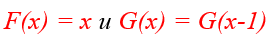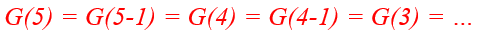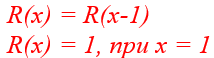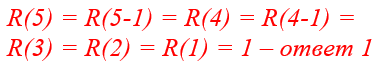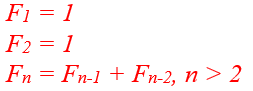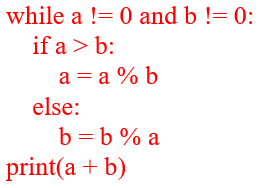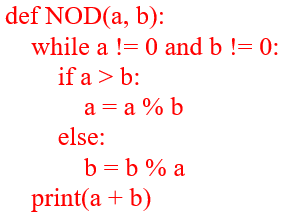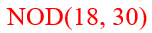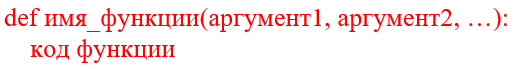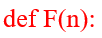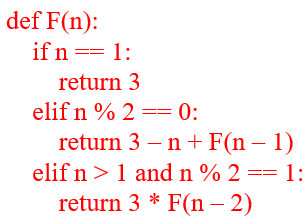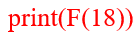Рекурсия

Задание на рекурсивный алгоритм в ЕГЭ по информатике (№16) оказывается для выпускников достаточно сложным – с прошлогодним вариантом этого задания справилась лишь половина. Это задание позиционируется составителями экзамена как задание повышенного уровня сложности, и этот факт делает его весьма необычным и достойным отдельного внимания. Цель этого раздела теории – познакомить вас с таким понятием, как рекурсия, и показать ключевые аспекты работы с рекурсивными алгоритмами. Но сначала – немного новой теории.

Математический смысл рекурсии

Рекурсия ­­­– это функция, которая обращается сама к себе при нахождении своего значения. Для того, чтобы лучше понять это определение сравним две функции:

Первая функция F(x) в качестве своего результата возвращает значение переменной x, т.е. F(0) = 0, F(3) = 3 и т.д. Со второй функцией всё немного сложнее. Чтобы посчитать, чему равно, например, G(5), нужно посчитать G(4), затем, чтобы посчитать G(4), нужно найти G(3) и т.д.:

Как можно заметить из примера, такая функция оказывается бесконечной и не приводит нас ни к какому чёткому ответу. Поэтому, чтобы рекурсивные функции имели смысл, для них указывают конечное условие, например:

Такая функция уже имеет смысл, так как она не является бесконечной. В тот момент, когда x будет равняться 1, мы уже не будем снова вызывать рекурсивную функцию, а просто воспользуемся её значением из конечного условия. Таким образом:

Известным примером из математики на рекурсивные функции, является алгоритм нахождения n-го члена последовательности Фибоначчи:

Чтобы посчитать n-й член последовательности, надо знать (n-1)-ый и (n-2)-ой члены. Для того, чтобы посчитать их, вы должны знать, в свою очередь, два предыдущих, и так далее. Но всегда должно быть какое-то изначальное, базовое значение – иначе вычислять рекурсию можно бесконечно, и в ней теряется всякий смысл.

Подпрограммы (функции) в языке Python

Теперь для того, чтобы перейти к рекурсиям в программировании, мы рассмотрим функции в языке Python и то, как их создавать.

Функции были придуманы с целью упрощения восприятия кода. Они позволяют уместить в себе какую-то часть программы, которая периодически встречается в коде, и обращаться к этому коду просто по вызову этой функции. Так, если в нашей программе мы часто считаем НОД двух чисел, то без использования функций нам придётся для каждого раза копировать вот такой кусочек кода:

При этом, допустим, этот фрагмент должен встречаться в нашей большой программе раз двадцать. Копировать его все двадцать раз не очень удобно – это делает программу громоздкой и неудобной. Чтобы избежать этого, были придуманы функции – именованные наборы команд, которые записываются один раз и могут быть вызваны из любого места в программе. Функции поддерживаются практически всеми языками программирования, правда синтаксис может немного различаться.

В языке Python, чтобы создать функцию, нам достаточно объявить её в программе с помощью кодового слова def, придумать ей имя, указать необходимое количество аргументов и описать алгоритм её работы. Для алгоритма нахождения НОД функция бы выглядела следующим образом:

Теперь, если нам в любом месте программы надо вызвать этот алгоритм для определенных значений a и b (например, 18 и 30), то следует написать всего одну строку:

В общем виде записать функцию можно так:

Рекурсивные функции

Теперь можем приступить непосредственно к самим рекурсивным функциям. В программировании за основу рекурсивных функций взят их математический смысл, поэтому в качестве примера составим рекурсивную функцию для уже известного нам алгоритма нахождения n-го члена последовательности Фибоначчи:

F₁ = 1

F₂ = 1

F_n = F_n-1 + F_n-2, n > 2

Решение будет следующим:

Команда return в коде означает «возврат» значения к той операции, которая вызвала функцию. Например, мы считаем 5-е число Фибоначчи и записываем значение в переменную A5:

Возврат значения и получение его переменной A5 возможно именно благодаря команде return.

№ 16 в ЕГЭ

В 16 задании формата ЕГЭ требуется определить, что выведет программа, содержащая рекурсивную функцию, при данном значении аргумента. Раньше значение аргумента, да и формат экзамена позволяли произвести вычисления без использования программ. Теперь же решать это задание на бумаге просто нецелесообразно. Именно поэтому будем учиться решать его при помощи составленной нами программы.

Рассмотрим форматное задание экзамена

Пример:

Алгоритм вычисления значения функции F(n), где n – натуральное число,

задан следующими соотношениями:

F(n) = 3 при n = 1;

F(n) = 3 – n + F(n − 1), если n – чётно,

F(n) = 3 * F(n − 2), если n > 1 и при этом n – нечётно.

Чему равно значение функции F(18)?

Решение:

Для начала объявим нашу функцию F(n):

Эта функция имеет несколько различных условий. Каждое условие будем обрабатывать при помощи условных операторов if, elif, else, и при выполнении определённого условия будем возвращать (оператор return) требуемое значение:

Вот и вся рекурсивная функция, которая нам потребуется для решения задания. Остаётся только вызвать эту функцию для требуемого значения аргумента n = 18 и показать на экране ответ:

Полная программа имеет вид:

После запуска нашей программы получаем на экране ответ – 19668.