Логические функции

В логике, помимо базовых логических операций, существуют еще другие. Для ЕГЭ необходимо и достаточно знать ровно две дополнительные логические операции – импликацию и эквиваленцию. Эти логические операции еще можно назвать составными, ведь они на самом деле состоят из базовых. Любую логическую операцию можно «разложить» на базовые – конъюнкцию, дизъюнкцию и инверсию. Выражение, связывающее логическую операцию с её разложением на базовые, называется равносильным выражением.

Импликация

Импликация по смыслу похожа на использование союзов «если… то…». Обозначается стрелкой от первой логической переменной ко второй: A → B. Для импликации равносильное выражение выглядит так:

A → B = ¬A \/ B

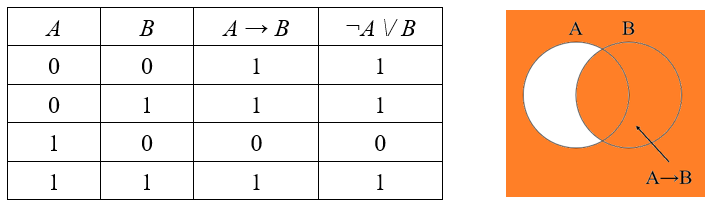
Это значит, что таблица истинности для A → B и для ¬A \/ B будет выглядеть идентично. Ниже приведена таблица истинности и диаграмма Эйлера для импликации:

Эквиваленция

Эквиваленция проверяет, одинаковы ли (эквивалентны ли) значения логических переменных – и выдает Истину, если одинаковы (1 и 1, 0 и 0) и Ложь, если не одинаковы (1 и 0, 0 и 1). Обозначается эквиваленция тремя полосами (как равно, только с еще одной чертой): A ≡ B. Для эквиваленции существует два равносильных выражения:

A ≡ B = (A /\ B) \/ (¬A /\ ¬B) = (¬A \/ B) /\ (A \/ ¬B)

Ниже приведена таблица истинности и диаграмма Эйлера для эквиваленции:

Порядок выполнения логических операций, содержащих импликацию и эквиваленцию

Если в выражении присутствует импликация и эквиваленция, то они выполняются всегда после базовых логических операций в таком порядке: сначала импликация, потом – эквиваленция. Таким образом, порядок выполнения всех логических операций будет выглядеть так:

1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Импликация
5. Эквиваленция

Скобки, разумеется, могут этот порядок менять.