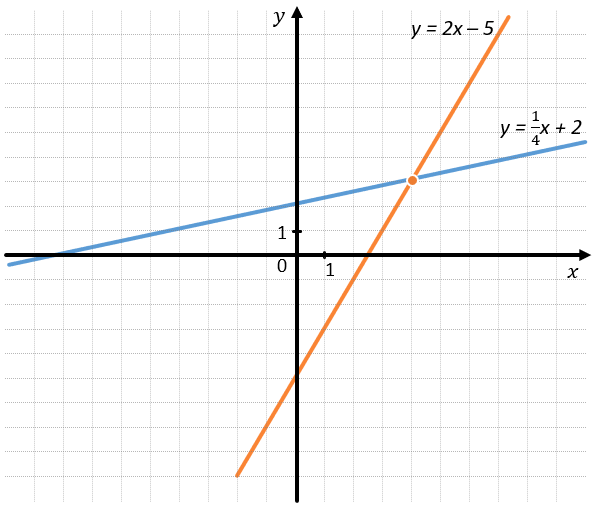Взаимное расположение графиков линейной функции
Взаимное расположение графиков линейной функции
График линейной функции представляет собой прямую. Если на одной координатной прямой существуют две прямые, то они, как и любые прямые на плоскости, могут пересекаться, быть параллельными друг другу или совпадать.
Рассмотрим две линейные функции:
\(y = k_{1}x + b_{1\ }\) и \(y = k_{2}x + b_{2}\)
И их возможные расположения на одной координатной плоскости.
СОВПАДЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций совпадают при:
\(k_{1} = k_{2}\)
\(b_{1} = b_{2}\)
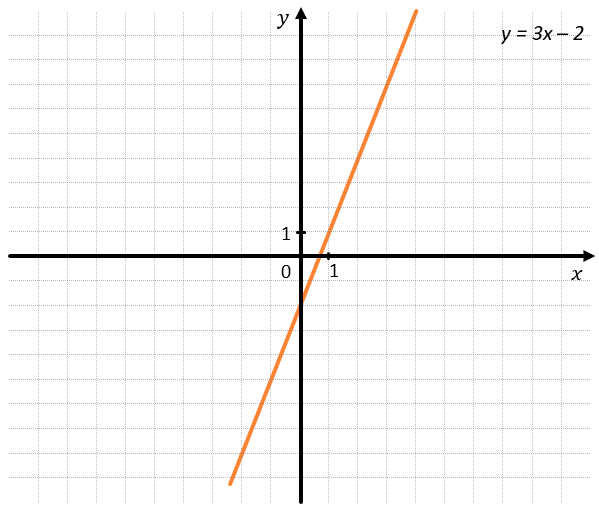
Например:
Графики функций \(y = 3x–2\) и \(y = 3x–2\) совпадают, так как
\(k_{1} = k_{2} = 3\ \) и \(\ b_{1} = b_{2} = \ –2\)
ПАРАЛЛЕЛЬНОСТЬ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций параллельны при:
\(k_{1} = k_{2}\)
\(b_{1} \neq b_{2}\)
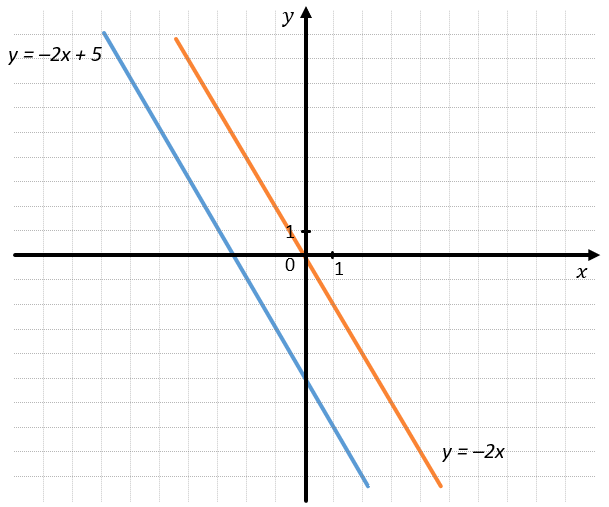
Например:
Графики функций \(y = –2x\) и \(y = –2x + 5\) параллельны, так как
\(k_{1} = k_{2} = \ –2\)
\(b_{1} = 0;\ b_{2} = 5 \Longrightarrow b_{1} \neq b_{2}\ \)
ПЕРЕСЕЧЕНИЕ ГРАФИКОВ ЛИНЕЙНОЙ ФУНКЦИИ:
Графики линейных функций пересекаются при:
\(k_{1} \neq k_{2}\ \) и \(\ b_{1} \neq b_{2}\)
Например:
Графики функций \(y = 2x–5\) и\(\ y = \frac{1}{4}x + 2\) пересекаются, так как
\(k_{1} = 2,\ k_{2} = \frac{1}{4} \Longrightarrow k_{1} \neq k_{2}\)
\(и\)
\(b_{1} = \ –5,\ b_{2} = 2 \Longrightarrow b_{1} \neq b_{2}\)
При этом по определению пересекающихся прямых, они должны иметь одну общую точку. Эта будет такая точка с координатами \((x;\ y)\), которая будет принадлежать как первому, так и второму графику функций.
То есть для функций:
\(y_{1} = k_{1}x_{1} + b_{1}\)
\(y_{2} = k_{2}x_{2} + b_{2}\)
Будут соблюдаться условия:
\(k_{1} \neq k_{2}\ \) и \(\ b_{1} \neq b_{2}\)
Поэтому будет существовать точка пересечения этих графиков с координатами:
\(x = x_{1} = x_{2}\)
\(y = y_{1} = y_{2}\)
В таком случае, чтобы найти точку пересечения графиков функций без построения для функций \(\mathbf{y}_{\mathbf{1}} = k_{1}x = b_{1}\) нужно:
1. Приравнять \(y_{1}\ и\ y_{2},\) а значит приравнять\(\ k_{1}x_{1} + b_{1}\ и\ k_{2}x_{2} + b_{2}.\)
2. Так как \(x_{1} = x_{2} = x\), решим уравнение
\(k_{1}x + b_{1} = k_{2}x + b_{2}.\)
3. Подставить найденный аргумент в любую из функций и найти её значение y. Найденная пара (x; y) будет являться координатой общей точки для данных графиков функций.
Рассмотрим данный алгоритм на примере функций, заданных на графике выше.
Найти без построений точку пересечения для графиков
\(y = 2x\ –\ 5\ \) и \(\ y = \frac{1}{4}x + 2\)
1. Игреки данных функций равны, следовательно:
\(2x\ –\ 5 = \frac{1}{4}x + 2\)
2. Иксы в данном уравнении равны, значит можем решить уравнение:
\(\frac{7}{4}x = 7\)
\(x = 4\)
3. Подставим x = 4 в первое уравнение, получим:
\(y = 2x\ –\ 5\)
\(y\ = \ 2 \bullet 4\ –\ 5\)
\(y = 3\)
Следовательно, точкой пересечения данных графиков является точка с координатами \((4;3)\), что и подтверждает наш график выше.
ЧАСТНЫЙ СЛУЧАЙ ПЕРЕСЕЧЕНИЯ ЛИНЕЙНЫХ ФУНКЦИЙ
Графики линейных функций пересекаются под прямым углом, если
\(k_{1} \bullet k_{2} = \ –1\)
\(k_{1} = \ –\frac{1}{k_{2}}\)
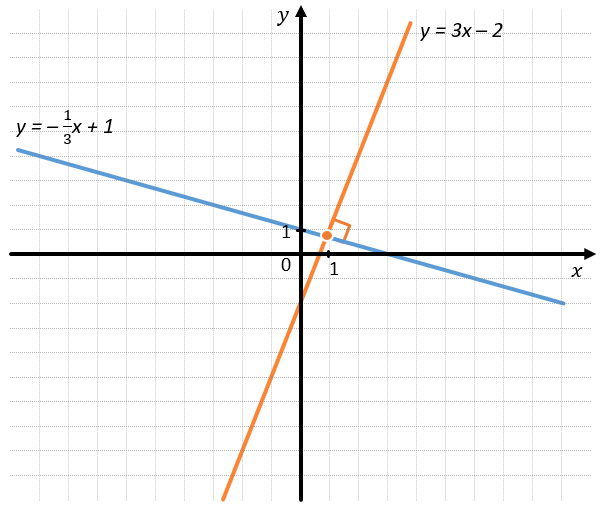
Например:
Графики функций \(y = 3x–2\) и \(y = \ –\frac{1}{3}x + 1\) перпендикулярны друг дугу, так как
\(k_{1} \bullet k_{2} = 3 \bullet (–\frac{1}{3}) = \ –1\)

Содержание