Квадратичная функция
Квадратичная функция
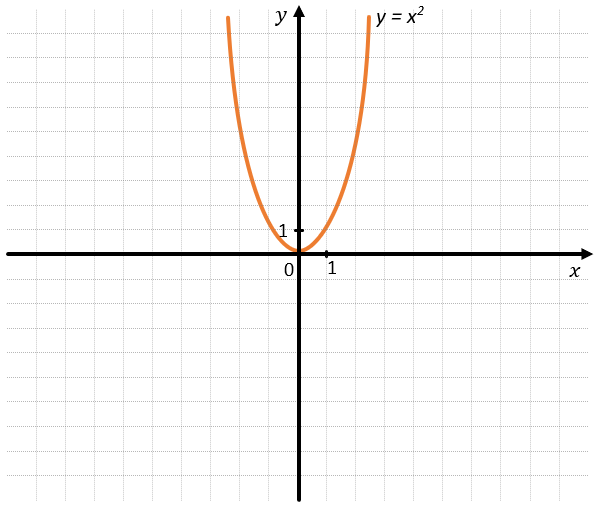
\(y = ax^{2} + \text{bx} + c,\) где \(a \neq 0\).
Графиком этой функции является парабола.
В этом виде функции \(a = 1,\ \ b = 0,\ \ c = 0.\)
В таком случае вершина параболы находится в точке \((0;0)\) и её ветви направлены вверх.
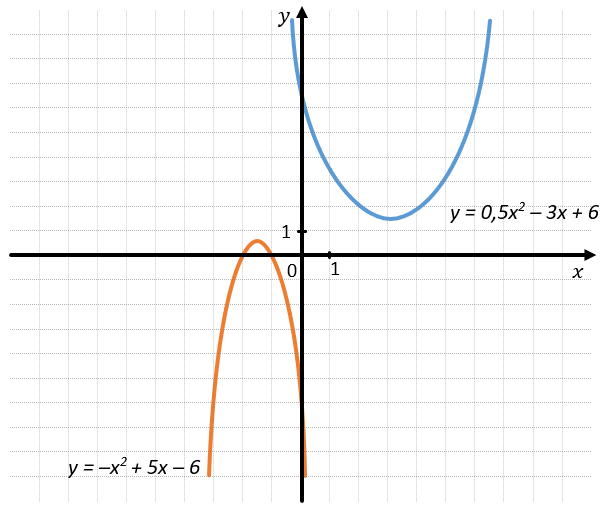
С изменением коэффициентов a, b и c меняется и внешний вид функции. Например:
ХАРАКТЕРИСТИКИ КВАДРАТИЧНОЙ ФУНКЦИИ:
| 1. Область определения: | \(D(y\mathbb{) = R}\) |
|---|---|
| 2. Область значений: | \(E(y\mathbb{) = R}\) |
| 3. Ограниченность и непрерывность: | Непрерывна |
| При \(a > 0\ \)ограничена снизу; При \(a < 0\) ограничена сверху. | |
| 4. Монотонность: | При \(a > 0\): убывает на \((–\infty;x_{верш})\) При \(a < 0\): возрастает на \((–\ \infty;\ x_{верш}) \)убывает на (\(x_{верш}; + \ \infty)\) |
| \(x_{верш} = \frac{–b}{2a}\) | |
| 5. Наибольшее и наименьшее значения | При \(a\ > \ 0:\) наименьшее значение в точке \((x_{верш};y_{верш})\) наибольшее значение отсутствует При \(a < 0\): наибольшее значение в точке \((x_{верш};y_{верш})\) наименьшее значение отсутствует |
| 6. Четность: | При \(b = 0\ \)четная При\(\ b \neq 0\ \)ни четная, ни нечетная |
| 7. Периодичность: | не периодичная |
| 8. Пересекает ось Ох | в точках \(\left( \frac{–b\ + \sqrt{D}}{2a};0 \right)\) и \(\left( \frac{–b\ –\ \sqrt{D}}{2a};0 \right)\), где \(D = b^{2}\ –4\text{ac}\) |
| 9. Пересекает ось Оу | в точке \((0;c)\) |
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ НА ВИД ЛИНЕЙНОЙ ФУНКЦИИ:
Коэффициент a:
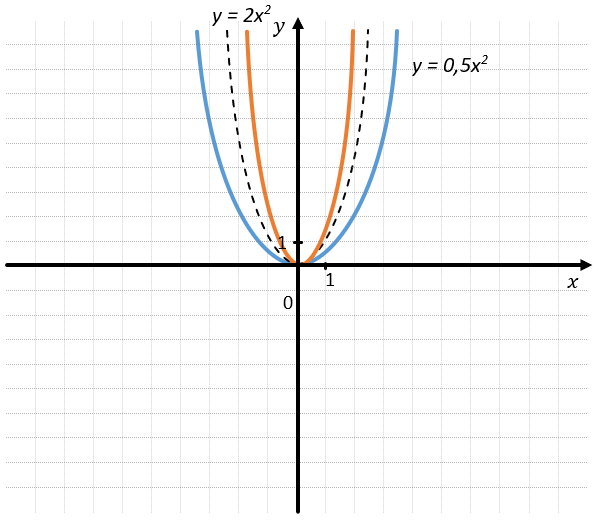
– При увеличении коэффициента a по модулю функция приближается к оси Оу.
– При уменьшении коэффициента a по модулю функция приближается к оси О
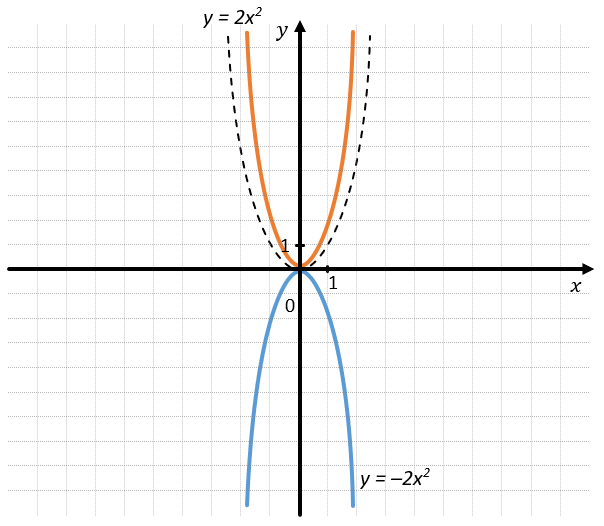
– При \(a > 0\) ветви параболы направлены вверх.
– При \(a < 0\) ветви параболы направлены вниз.
Коэффициент b:
По коэффициенту можно определить координаты вершины параболы – точки, где соединяются две её ветви.
\({x_{верш} = \frac{–b}{2a} }{y_{верш} = f(x_{верш})}\)
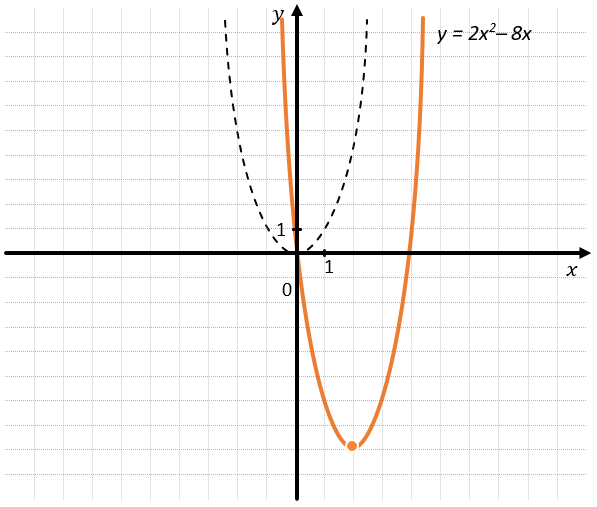
\(x_{верш} = \frac{–b}{2a} = \frac{–\left( –8 \right)}{4} = 2\)
\(y_{верш} = f(2) = 2 \bullet 2^{2}\ –8 \bullet 2 = 8\ –\ 16 = \ –8\)
Точка вершины с координатами \((2;\ –8)\)
– Если a и b имеют разные знаки, тогда вершина параболы находятся справа от Oy.
– Если a и b и имеют одинаковые знаки, то вершина параболы находится слева от Oy.
Коэффициент c:
График функции пересекает ось Oy в точке \((0;c).\)
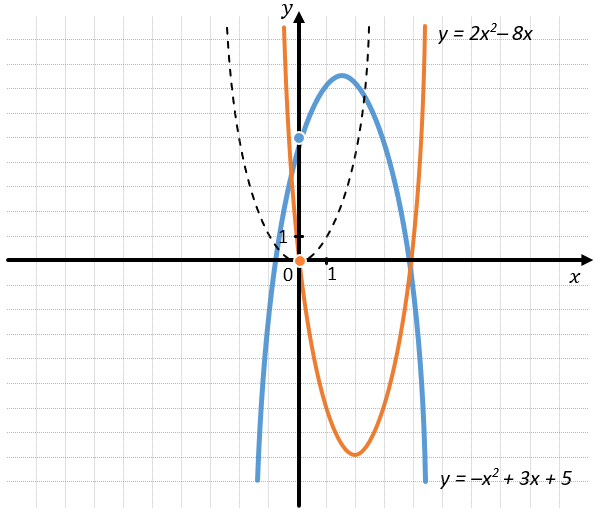
График \(y = 2x^{2}\ –\ 8\) пересекает ось Оу в точке (0;0).
График \(y = \ –x^{2} + 3x + 5\) пересекает ось Оy в точке (0;5).
ДИСКРИМИНАНТ:
Дискриминант зависит от всех трёх коэффициентов квадратичной функции и равен:
\(D = b^{2}\ –ac\ \)
От дискриминанта зависит, сколько корней имеет уравнение \(ax^{2} + \text{bx} + c = 0\). Это значит, что эти корни являются точками пересечения параболы с осью Ох (т. к. ось Ох – это прямая \(у = 0\)). Получается, что дискриминант показывает, количество таких пересечений:
– При \(D > 0\) парабола пересекает ось Ох два раза (уравнение имеет два корня);
– При \(D = 0\) парабола пересекает ось Ох один раз – это вершина параболы (уравнение имеет один корень);
– При\(\ D < 0\) парабола не пересекает ось Ох (уравнение не имеет корней).
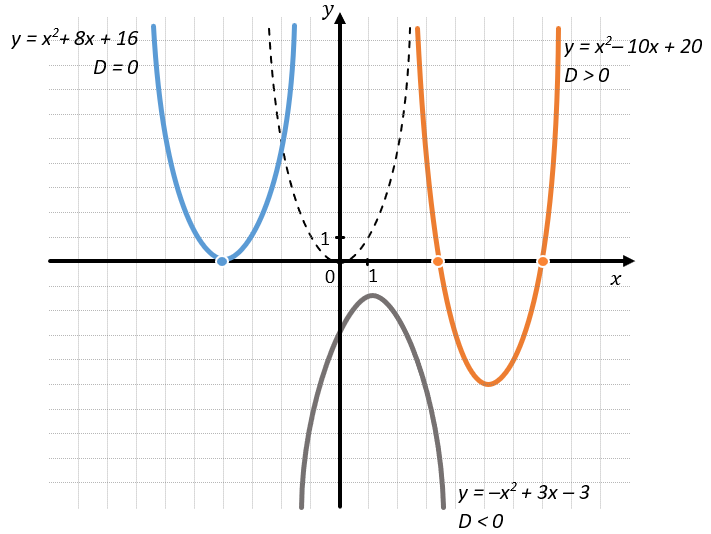
Рассмотрим три функции и их дискриминанты:
\({1.\ \ y\ = \ –\ x^{2} + 3x + 5 }{D = 9\ + 20 = 29\ > \ 0}\)
\({2.\ \ y = x^{2} + 8x + 16 }{D = 64\ –64 = 0}\)
\({3.\ \ y = 2x^{2} + 3x + 4 }{D = 9\ –32 = \ –23 < 0}\)
Действительно, графики этих функций будут иметь разное количество точек пересечения с осью Ох:

Содержание