Угол между скрещивающимися прямыми

Хотите улучшить свои результаты?

Получите SMART-набор в подарок и прокачайтесь на максимум! 🎁

Забрать подарки

imageDesktop

Угол между скрещивающимися прямыми

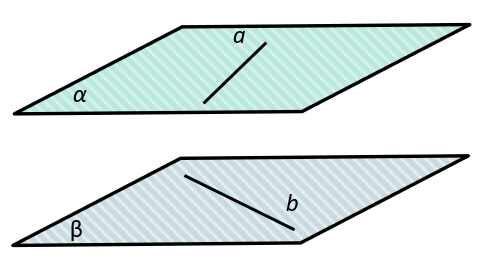
Скрещивающиеся прямые – это прямые, которые не лежат в одной плоскости и не параллельны. Для таких прямых не существует плоскости, которая бы их содержала.

Чтобы найти угол между скрещивающимися прямыми, нужно знать, что через каждую из двух скрещивающихся прямых можно провести плоскость, параллельную второй прямой, при том только одну.

\(a ∸ b\) – скрещивающиеся прямые

\(a \in \alpha,\ b \in \beta\)

\(\alpha \parallel \beta\)

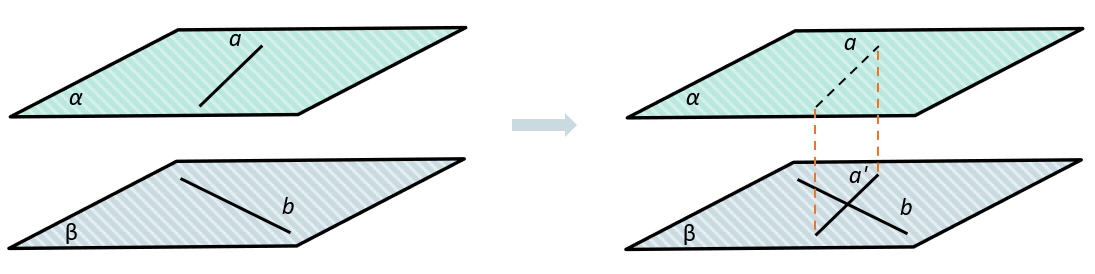
Чтобы найти угол между скрещивающимися прямыми, нужно найти угол между одной прямой и проекцией другой прямой. Для этого нужно:

Параллельным переносом перенести одну прямую на плоскость, содержащую вторую прямую.

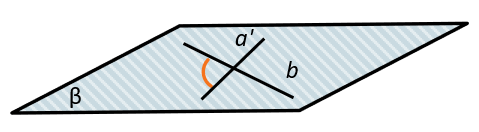
Найти угол между прямыми на этой плоскости:

Пример:

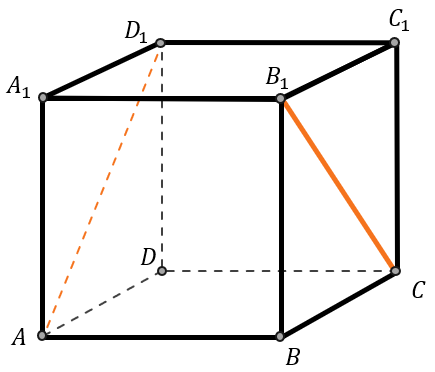
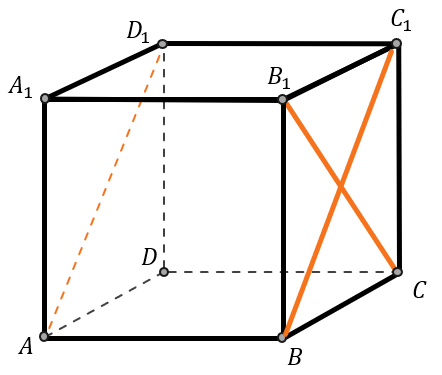
Дан куб \(\text{ABCD}A_{1}B_{1}C_{1}D_{1}\). Найдите угол между \(AD_{1}\) и \(B_{1}С\).

Сделаем чертеж и обозначим прямые, между которыми нам нужно найти угол:

Так как у куба стороны попарно параллельно, перенесем отрезок \(AD_{1}\) на плоскость \(BB_{1}C_{1}\).

Получим два пересекающихся отрезка \(B_{1}C\) и \(BC_{1}\), угол между которыми равен углу между \(AD_{1}\) и \(B_{1}С\).

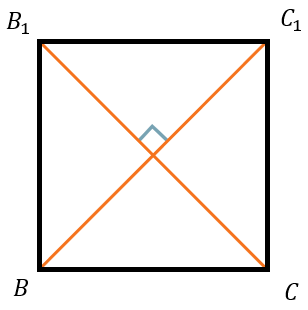
Найдем угол между \(B_{1}C\) и \(BC_{1}\) – это диагонали стороны куба \(BB_{1}C_{1}C\), а так как все стороны куба являются квадратами, угол между ними равен \(90{^\circ}\):

Ответ: 90°.

play

Урок пройден! Продолжай изучать предмет дальше -> там интересно :)

Следующие темы

Графики тригонометрических функций Графическое применение производной Интеграл

Анализ функций

Графики тригонометрических функций Графическое применение производной Интеграл Первообразная Правила дифференцирования Преобразование графиков функции Свойства функций Смысл производной Экстремумы

Неравенства

Иррациональные неравенства Метод рационализации неравенств Неравенства с модулем Показательные и логарифмические неравенства Простейшие неравенства Рациональные неравенства Системы и совокупности неравенств Тригонометрические неравенства

Планиметрия

Биссектриса Векторы Виды треугольников Высота Движения Квадрат Комбинации с окружностью Медиана Метод координат на плоскости Многоугольники Окружнoсть и круг Отношения в геометрии Параллелограммы Площади четырёхугольников Площадь круга и сектора круга Подобие фигур Простейшие расстояния на плоскости Прямоугольник Прямые и углы на плоскости Равенство фигур Ромб Серединный перпендикуляр Симметрия Скалярное произведение векторов Соотношение между сторонами и углами в треугольнике Средняя линия Теорема Менелая и теорема Чевы Теорема Пифагора Теорема синусов и теорема косинусов Теорема Фалеса и теорема о пропорциональных отрезках Трапеция Треугольники. Площади Четыре замечательные точки треугольника Элементы планиметрии

Реальная математика

Вероятность Диаграммы, графики и таблицы Комбинаторика Метод математической индукции Множества Основы комбинаторики Прикладные задачи Сложные проценты Текстовые задачи на движение по воде Текстовые задачи на движение по окружности Текстовые задачи на движение по прямой Текстовые задачи на производительность Текстовые задачи на проценты Текстовые задачи на сплавы и смеси

Стереометрия

Векторы в пространстве Движения в пространстве Двугранный угол Метод координат в пространстве Параллельность прямых и плоскостей Перпендикулярность прямых и плоскостей Пирамиды Призмы Расстояние между скрещивающимися прямыми Расстояние от прямой до плоскости Расстояние от точки до плоскости Сечения в многогранниках Сечения в телах вращения Тела вращения Теорема о трёх перпендикулярах Угол между плоскостями Угол между прямой и плоскостью Угол между скрещивающимися прямыми Элементы и аксиомы стереометрии

Уравнения

Дробно-рациональные уравнения Иррациональные уравнения Квадратные уравнения Линейные уравнения Логарифмические уравнения Методы решения уравнений Однородные уравнения Отбор корней с помощью графиков тригонометрических функций Отбор корней с помощью двойного неравенства Отбор корней с помощью тригонометрического круга Показательные уравнения Простейшие тригонометрические уравнения Системы и совокупности уравнений с одной переменной Системы уравнений с двумя переменными Уравнения в целых числах Уравнения высших степеней Уравнения с модулем

Формулы и выражения

Иррациональные выражения Логарифмические выражения и свойства логарифмической функции Показательные выражения и свойства показательной функции Свойства степеней Степени Тригонометрический круг Формулы тригонометрии

Заберите SMART-набор в подарок и улучшите свои результаты🧡

Поделитесь своими контактами и получите:

Топовые курсы по профориентации и поступлению
Лайфхаки по подготовке к ЕГЭ
Скидки до -44%

Как еще с нами можно связаться

Как еще с нами можно связаться

Содержание