Неравенства с модулем

Неравенства с модулем

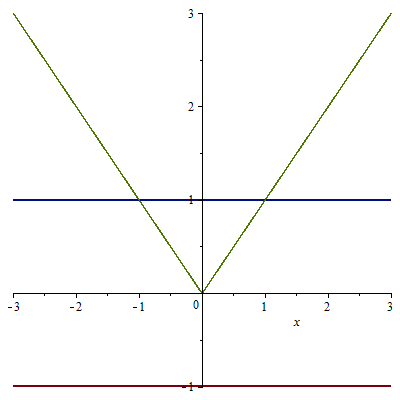
Изобразим график функции $y = |x|$ и несколько прямых, параллельных оси Ох.

Модуль больше отрицательного числа. Модуль меньше отрицательного числа.

Глядя на график, легко убедиться, что если неравенство имеет вид $\left| x \right| > - 1$ , то его решением будет любое число.

В тоже время неравенство $\left| x \right| < - 1$ решение иметь не будет, так как неотрицательное число не может быть меньше отрицательного.

Модуль больше положительного числа. Модуль меньше положительного числа.

Теперь сравним модуль с положительным числом. Рассмотрим такой пример: $\left| x \right| < 1$. На графике это соответствует нижней части «уголка».

Раскроем модуль как обычно.

На положительном промежутке числовой прямой раскрываем модуль с изначальным знаком:

$\left\{ \begin{matrix} \ \\ x \geq 0 \\ x < 1 \\ \ \\ \end{matrix} \right.\$ $\rightarrow x \in \lbrack 0;1)$

На отрицательном промежутке числовой прямой раскрываем модуль с противоположным знаком:

$\left\{ \begin{matrix} \ \\ x < 0 \\ - x < 1 \\ \ \\ \end{matrix} \right.\$

Имеем $\left\{ \begin{matrix} \ \\ x < 0 \\ x > - 1 \\ \ \\ \end{matrix} \right.\$ $\rightarrow x \in ( - 1;0)$.

Мы рассматривали 2 случая, то есть формально получили совокупность двух систем.

$\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x \geq 0 \\ x < 1 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x < 0 \\ x > - 1 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

Значит, решения, полученные в каждом случае, необходимо объединить.

Получим, что $x \in ( - 1;1)$

В общем виде решение неравенства, вида $\left| f\left( x \right) \right| < a$ будет иметь вид:

$\left| f\left( x \right) \right| < a \Longleftrightarrow \left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ f\left( x \right) < a \\ f(x) \geq 0 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ - f\left( x \right) < a \\ f\left( x \right) < 0 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

$\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ f\left( x \right) < a \\ f(x) \geq 0 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ f\left( x \right) > - a \\ f\left( x \right) < 0 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \Longleftrightarrow - a < f\left( x \right) < a$

Более кратко имеем:

$|f\left( x \right)| \leq a \Longleftrightarrow - a < f\left( x \right) < a$

Теперь давайте перейдем к неравенству вида $\left| x \right| > 1$. На графике ему соответствуют «рожки». Раскроем модули для каждого случая.

На положительном промежутке числовой прямой раскрываем модуль с изначальным знаком

$\left\{ \begin{matrix} \ \\ x \geq 0 \\ x > 1 \\ \ \\ \end{matrix} \right.\ \rightarrow x \in (1; + \infty)$

На отрицательном промежутке числовой прямой раскрываем модуль с противоположным знаком:

$\left\{ \begin{matrix} \ \\ x < 0 \\ - x > 1 \\ \ \\ \end{matrix} \right.\$ Имеем $\left\{ \begin{matrix} \ \\ x < 0 \\ x < - 1 \\ \ \\ \end{matrix} \right.\ \rightarrow x \in ( - \infty;1)$

Теперь нам опять оба случая необходимо объединить совокупностью и затем объединить решения.

$\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x \geq 0 \\ x > 1 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x < 0 \\ x < - 1 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

Тогда $x \in ( - \infty;1) \cup (1; + \infty)$.

Этот результат соответствует тому, что видно на графике.

В общем виде решение неравенства, вида $\left| f\left( x \right) \right| > a$ будет иметь вид:

$\left| f\left( x \right) \right| > a \Longleftrightarrow \left\lbrack \begin{matrix} \text{\ \ } \\ \left\{ \begin{matrix} \ \\ f\left( x \right) > a \\ f(x) \geq 0 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ - f\left( x \right) > a \\ f\left( x \right) < 0 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

$\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ f\left( x \right) > a \\ f(x) \geq 0 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ f\left( x \right) < - a \\ f\left( x \right) < 0 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \Longleftrightarrow \left\lbrack \begin{matrix} \ \\ f\left( x \right) > a \\ f\left( x \right) < - a \\ \ \\ \end{matrix} \right.\$

Более кратко имеем:

$\left| f\left( x \right) \right| > a \Longleftrightarrow \left\lbrack \begin{matrix} \ \\ f\left( x \right) > a \\ f\left( x \right) < - a \\ \ \\ \end{matrix} \right.\$

Несколько модулей

Неравенство может так же содержать несколько модулей.

$\left| f\left( x \right) \right| + \left| g\left( x \right) \right| + \ldots + \left| p\left( x \right) \right| < a$ или $\left| f\left( x \right) \right| + \left| g\left( x \right) \right| + \ldots + \left| p\left( x \right) \right| > a$.

Для решения такого вида неравенств следует воспользоваться алгоритмом:

1. Определить критические точки и разделить прямую на промежутки;

2. В каждом из промежутков раскрыть модуль с соответствующим знаком;

3. Для каждого случая решить систему неравенств;

4. Объединить полученные результаты.

Пример.

$\left| x + 3 \right| + \left| 2x - 1 \right| > 5$

1. Определим критические точки:

$x + 3 = 0 \rightarrow x = - 3$

$2x - 1 = 0 \rightarrow x = 0,5$

Таким образом имеем 3 промежутка: $x \in \left( - \infty; - 3 \right\rbrack;x \in \left( - 3;0,5 \right\rbrack;x \in (0,5;\ + \infty)$.

2. $\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x \in ( - \infty; - 3\rbrack \\ - x - 3 - 2x + 1 > 5 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x \in ( - 3;0,5\rbrack \\ x + 3 - 2x + 1 > 5 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x \in (0,5;\ + \infty) \\ x + 3 + 2x - 1 > 5 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

3. Решим каждую из полученных систем:

$\left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x \in ( - \infty;\ - 3\rbrack \\ - 3x > 7 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x \in ( - 3;0,5\rbrack \\ - x > 1 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x \in (0,5;\ + \infty) \\ 3x > 3 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \ \rightarrow \left\lbrack \begin{matrix} \ \\ \left\{ \begin{matrix} \ \\ x \in ( - \infty;\ - 3\rbrack \\ x < \frac{7}{3} \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x \in ( - 3;0,5\rbrack \\ x < - 1 \\ \ \\ \end{matrix} \right.\ \\ \left\{ \begin{matrix} \ \\ x \in (0,5;\ + \infty) \\ x > 1 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\$

4. Объединим полученные результаты:

$\left\lbrack \begin{matrix} \ \\ x \in ( - \infty; - 3\rbrack \\ x \in ( - 3; - 1) \rightarrow x \in ( - \infty; - 1) \cup (1; + \infty) \\ x \in (1; + \infty) \\ \ \\ \end{matrix} \right.\$.

Возведение в квадрат

Неравенства вида $\left| f\left( x \right) \right| < \left| g\left( x \right) \right|$ решают возведением в квадрат обеих частей.

Пример.

$\left| x + 3 \right| < \left| x - 1 \right|$

$\left( x + 3 \right)^{2} < \left( x - 1 \right)^{2}$

$x^{2} + 6x + 9 < x^{2} - 2x + 1$

$6x + 2x < 1 - 9$

$8x > - 8$

$x > - 1$