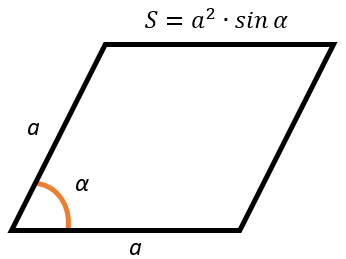Ромб

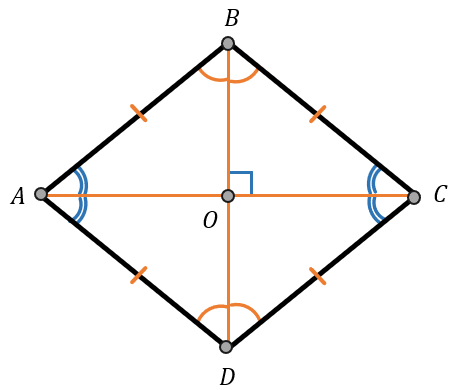
РОМБ

$AB = BC = CD = DA$

СВОЙСТВА И ПРИЗНАКИ РОМБА

Можно сказать, что ромб – это частный случай параллелограмма, поэтому он будет обладать всеми свойствами и признаками параллелограмма, но при этом имеет свои:

Свойства ромба:

Ромб обладает всеми свойствами параллелограмма, а также:

1. Диагонали ромба перпендикулярны друг другу:

$АС\bot\text{BD}$

2. Диагонали ромба являются биссектрисами углов, из которых выходят:

$\angle BAC = \angle CAD$

$\angle ADB = \angle BDC$

$\angle ABD = \angle DBC$

$\angle BCA = \angle ACD$

Признаки ромба:

Четырехугольник является ромбом, если обладает хотя бы одним свойством параллелограмма и одним из свойств ромба:

1. Две его смежные стороны равны:

$\mathbf{AB = BC}$

$или$

$\mathbf{BC = CD}$

2. Его диагонали пересекаются под прямым углом:

$АС\bot\text{BD}$

3. Одна из диагоналей делит содержащие её углы пополам:

$\angle BAC = \angle CAD$

$или$

$\angle ADB = \angle BDC$

4. Все высоты равны.

ПЛОЩАДЬ РОМБА

Площадь ромба находится также, как площадь параллелограмма, но из-за необычных свойств, формулы нахождения его площади можно упростить.

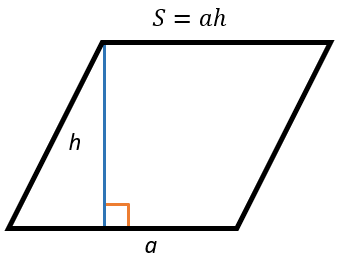
1. Через высоту и сторону

Площадь ромба равна произведению его стороны на высоту (при чем для любой стороны это выражение будет одинаковым, так как стороны равны)

2. Через сторону и угол между сторонами

Площадь ромба равна произведению квадрата его стороны на синус угла между сторонами.

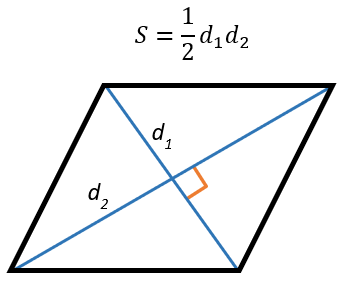
3. Через диагонали

Площадь ромба равна половине произведения его диагоналей.