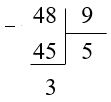Смешанные дроби и действия с ними
Смешанные дроби и действия с ними
Неправильная дробь – это дробь, числитель которой больше знаменателя. В таком случае у дроби выделяется целая часть и её можно записать в виде смешанной.
Например,
\(\frac{7}{4} = \frac{4}{4} + \frac{3}{4} = 1 + \frac{3}{4} = 1\frac{3}{4}\)
1 – целая часть, а \(\frac{3}{4}\) – дробная часть смешанного числа \(1\frac{3}{4}\).
АЛГОРИТМ ПЕРЕВОДА НЕПРАВИЛЬНОЙ ДРОБИ В СМЕШАННУЮ:
-
Разделить числитель на знаменатель в столбик с остатком.
-
Неполное частное будет целой частью.
-
Остаток (если он есть) станет числителем дробной части смешанной дроби, а делитель - знаменателем.
Например,
Переведем неправильную дробь \(\frac{48}{9}\) в смешанную:
Неполное частное \(= 5\), остаток \(= 3,\) делитель \(= 9\), тогда эту неправильную дробь можно записать как: \(5\frac{3}{9}\).
АЛГОРИТМ ПЕРЕВОДА СМЕШАННОЙ ДРОБИ В НЕПРАВИЛЬНУЮ:
-
Перемножить целую часть со знаменателем дробной части.
-
К полученному произведению прибавить числитель дробной части.
-
Записать полученную сумму в числитель неправильной дроби, а знаменатель оставить без изменений.
Например,
Переведем смешанную дробь \(4\frac{5}{7}\) в неправильную:
Числитель неправильной дроби будет равен
\((4 \bullet 7) + 5 = 28 + 5 = 33\).
Знаменатель останется прежний и будет равен 7.
Получим: \(4\frac{5}{7} = \frac{33}{7}\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ДРОБЕЙ:
При сложении и вычитании смешанных чисел отдельно складывают целые части, отдельно дробные по правилам сложения обыкновенных дробей.
-
Если суммой дробных частей является неправильная дробь, то из нее выделяют целую часть и прибавляют к сумме целых частей.
Например:
\(5\frac{3}{8} + 2\frac{6}{8} = (5 + 2) + (\frac{3}{8} + \frac{6}{8}) = 7 + \frac{9}{8} = 7 + 1\frac{1}{8} = 8\frac{1}{8}\)
-
Если при вычитании дробная часть уменьшаемого меньше дробной части вычитаемого, то поступают так:
\(7\frac{3}{5}\ –\ 2\frac{4}{5} = (7 + \frac{3}{5})\ –\ 2\frac{4}{5} = (6 + 1 + \frac{3}{5})\ –\ 2\frac{4}{5} = (6 + 1\frac{3}{5})\ –\ 2\frac{4}{5} = (6 + \frac{8}{5})\ –\ 2\frac{4}{5} = 6\frac{8}{5} + 2\frac{4}{5}\)
Таким образом мы выделили из целой части единицу и прибавили её к дробной. Теперь можно считать разность:
\(7\frac{3}{5}\ –\ 2\frac{4}{5} = 6\frac{8}{5} + 2\frac{4}{5} = (6\ –\ 2) + (\frac{8}{5}\ –\ \frac{4}{5}) = 4 + \frac{4}{5} = 4\frac{4}{5}\)
-
Так же поступают при вычитании смешанной дроби из целого числа.
Например:
\(3\ –\ 1\frac{2}{6} = (2 + \frac{6}{6})\ –\ 1\frac{2}{6} = (2\ –\ 1) + (\frac{6}{6}\ –\ \frac{2}{6}) = 1\frac{4}{6}\)

Наши социальные сети
Подписывайся!
Экономь время
на подготовке в ТГ
Забирай полезные чек-листы, памятки и лайфхаки
Подписаться →

Изучай новое
без усилий в ВК
Смотри полезные видео и вебинары, где объясняем сложное простым языком
Подписаться →

Забирай полезное в Максимум БЛОГЕ
Узнай первым лайфхаки по решению заданий предстоящего экзамена
Подписаться →

Содержание