Простейшие неравенства
Простейшие неравенства
Неравенства используются для сравнения чисел и выражений. Можно сравнивать числа и делать вывод об их расположении на числовой прямой относительно друг друга. Неравенство \(7 > 5\) означает, что число 7 лежит правее числа 5 на координатной оси:
Так же можно сравнивать самые разные выражения, например
\(x \geq 5\), или \(x^{2} + 2x > 4x + 5\).
В таком случае говорят о множестве решений неравенства, то есть о всех значениях переменной, для которой данное неравенство выполняется (в некоторых случаях это множество может состоять из одной точки или вообще быть пустым).
ОБОЗНАЧЕНИЕ НЕРАВЕНСТВ:
Неравенства можно обозначать четырьмя способами:
-
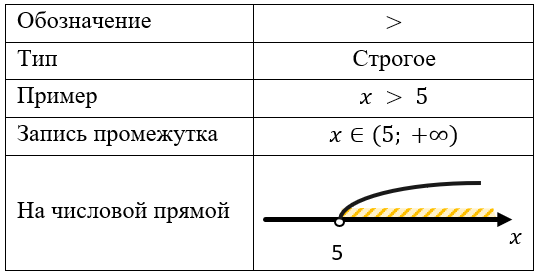
Больше
-
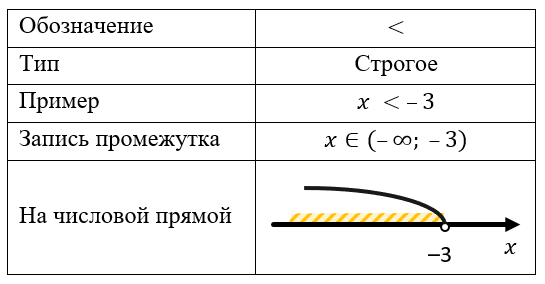
Меньше
-
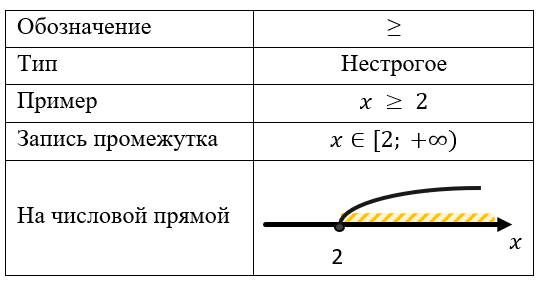
Больше или равно:
-
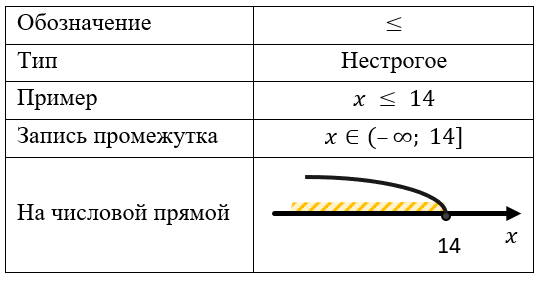
Меньше или равно:
Если неравенство строгое, то граничная точка в решение не входит (поэтому ее «выкалывают» на координатной оси).
ДВОЙНЫЕ НЕРАВЕНСТВА:
Виды двойных неравенств не отличаются от видов обыкновенных, разница лишь в том, что промежуток обозначается уже двумя числами, а не одним.
Например:
\(1 < x \leq 4\)
Эта запись обозначает, что x больше 1 и при этом меньше либо равно 4.
1. Числовой промежуток будет записываться в соответствии со строгостью знаков к определенным числам. Скобка возле числа 1 будет круглой, а возле числа 4 – квадратной:
\(x \in (1;4\rbrack\)
2. Аналогично строгости знаков и виду скобок на числовой прямой будут закрашены или не закрашены точки. Число 1 будет отмечаться выколотой точкой, а число 4 закрашенной. Тогда на координатной прямой это двойное неравенство будет выглядеть так:
ПРАВИЛА ПРЕОБРАЗОВАНИЯ НЕРАВЕНСТВ:
1. Любое слагаемое в неравенстве можно перенести из одной части уравнения в другую, изменив его знак на противоположный:
\({x + 5 > 0 }{x > \ –5}\)
2. Можно умножать и делить левую и правую части уравнения на одно и то же положительное число:
\({2y > \left. \ 16 \right| : 2 }{y > 8}\)
3. Можно умножать и делить левую и правую части уравнения на одно и то же отрицательное число, заменяя при этом знак неравенства на противоположный:
\({–\frac{t}{2} \leq \left. \ 10 \right| \bullet \left( –2 \right) }{t \geq \ –20}\)
4. Для двойных неравенств соблюдаются те же правила, с разницей в том, что алгебраические преобразования производятся сразу над всеми его частями:
\({2 \leq x + 5 \leq 8 }{–3 \leq x \leq 3}\)
5. Как и в уравнениях можно раскрывать скобки и упрощать выражения во всех частях неравенства или, наоборот, раскладывать на множители.
Решить неравенство:
\(5(1\ –\ x) < 12\)
1. Преобразуем неравенства так, чтобы с одной стороны было только выражение, содержащее переменную, а с другой только число:
\(5(1\ –\ x) < 12\)
\(5\ –\ 5x < 12\)
\(–5x < 7\)
2. Делим на коэффициент перед переменной, при необходимости меняя знак на противоположный:
\(–5x < \left. \ 7 \right| : (–5)\)
\(x > \ –1,4\)
Ответ: \(x \in (–1,4; + \infty)\).

Содержание