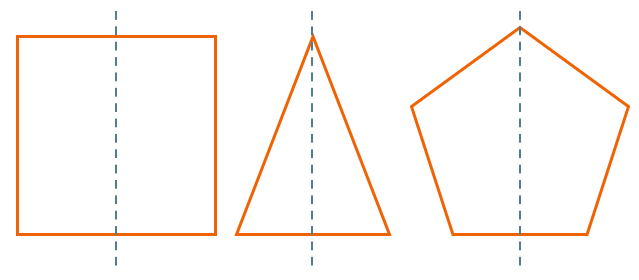Симметрия

Симметрия

Симметрия бывает лучевая (через прямую) и центральная (через точку)

ЛУЧЕВАЯ СИММЕТРИЯ

Например,

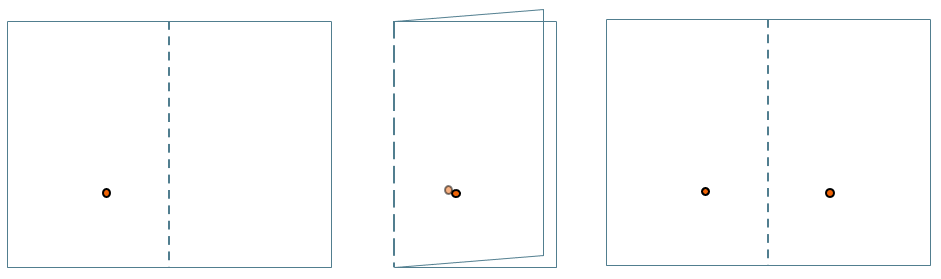
Возьмем лист бумаги и отметим на нём точку. Сложим лист бумаги по линии. Тогда наша точка «отпечатается» на противоположной стороне от нее:

Линия сгиба и будет линией симметрии. Говорят, что точка симметрична относительно данной прямой.

Мы можем отражать любые точки относительно любых прямых, например:

Чтобы каждый раз не складывать мысленно листок бумаги, можно использовать общий принцип образования лучевой симметрии.

Чтобы отразить точку относительно линии симметрии нужно:

1. Провести перпендикуляр от точки до линии симметрии. Получится отрезок от точки до линии.
2. Продлить этот отрезок в два раза, чтобы линия симметрии оказалась на его середине.
3. На конце продленного отрезка будет находиться точка, симметричная данной.

Например,

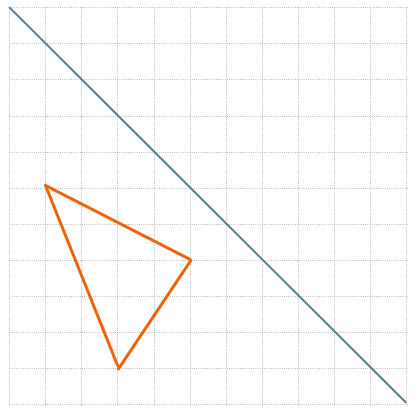
Отразите треугольник относительно заданной линии симметрии.

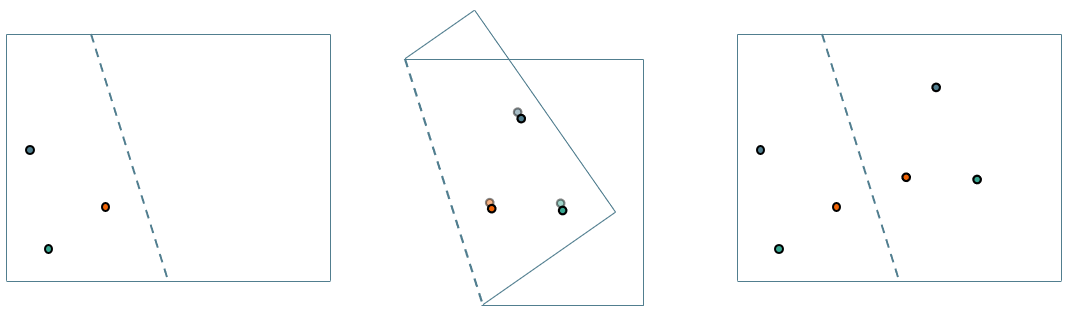
1. Чтобы отразить весь треугольник, нужно отразить каждую её точку. Отразим три вершины треугольника.
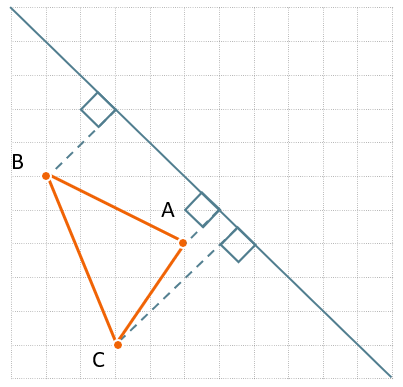
2. Проведем от каждой точки перпендикуляр к линии симметрии.
3. Посчитаем длины этих перпендикуляров до каждой точки:

От точки А – 1 диагональ клетки

От точки В – 2 диагонали клетки

От точки С – 3 диагонали и еще половина

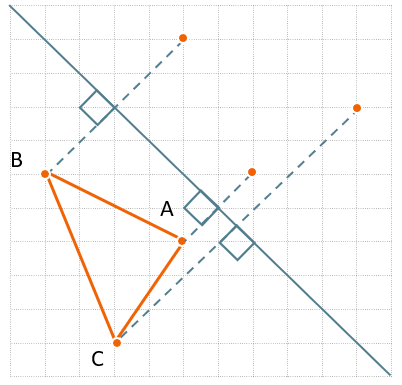
4. Продлим каждый перпендикуляр на такую же длину. Получили что от каждой точки до их «отражений» будет:

От А – 2 диагонали

От В – 4 диагонали

От С – 7 диагоналей

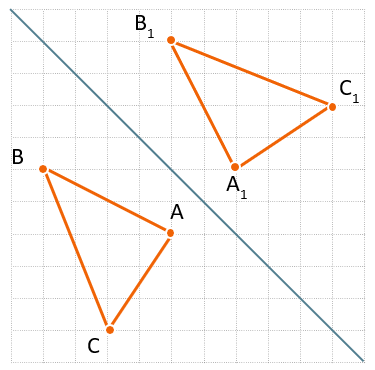
5. Соединим получившиеся точки на другой стороне от линии симметрии и получим треугольник симметричный данному.

\(\Delta АВС\ симметричен\ \Delta A_{1}B_{1}C_{1}\) по линии симметрии

СИММЕТРИЯ ФИГУР

Линию симметрии внутри фигуры называют осью симметрии.

Например:

Данные фигуры симметричный относительно своих осей симметрии:

А вот эти фигуры несимметричные. У них не осей симметрии такие фигуры называют ассиметричными:

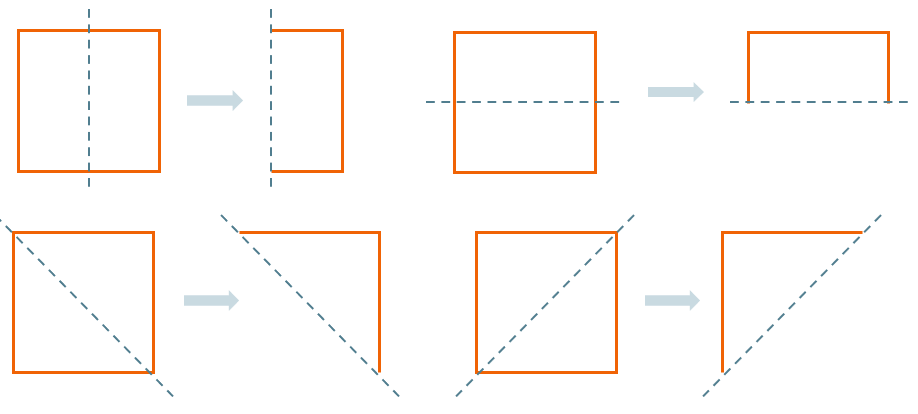
При этом у одной фигуры может быть несколько осей симметрии. Например, у квадрата их четыре:

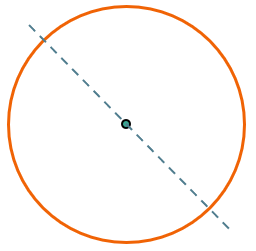
А вот у окружности есть бесконечное количество осей симметрии, т.к. любая прямая, проведенная через центр окружности, является осью её симметрии:

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

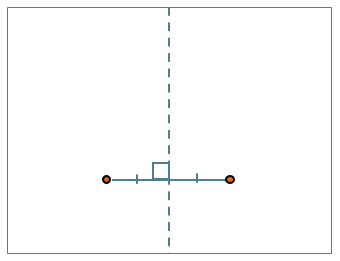
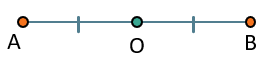
Такая симметрия выстраивается аналогично лучевой симметрии, только теперь нужно проводить отрезок от точки к точке (без перпендикуляров) и продолжать этот отрезок на такую же длину. Например:

Точка В симметрична точке А относительно точки О.

Если все центральные симметрии фигуры пересекаются в одной точке, то такая точка называется центром фигуры.

Фигура, которая имеет центр, при повороте на 180⁰ совпадает сама с собой.

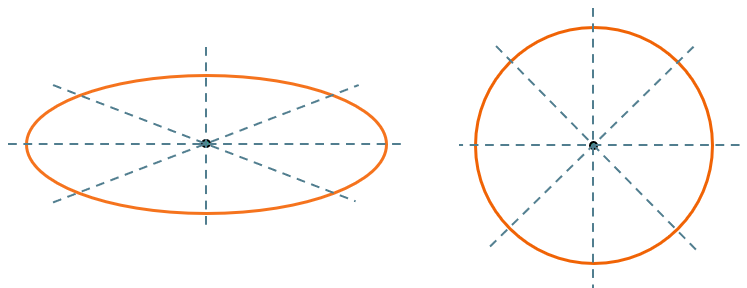
Например, любой овал или окружность имеют центр:

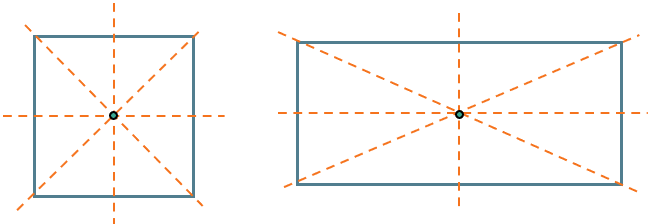
Прямоугольник и квадрат тоже имеют свои центры: