Интернет-энциклопедия по школьным предметам от Maximum Education. Учебник поможет решить домашнее задание, подготовиться к контрольной и вспомнить прошлые темы.
Индукция
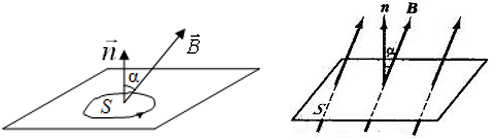
Магнитный поток, проходящий через площадь S равен Ф = BS cosα, где:
Ф ― величина магнитного потока, [Вб];
S ― площадь контура, [м2];
B ― индукция магнитного поля, [Тл];
α ― угол между нормалью \(\overrightarrow{n}\) к площади контура и вектором индукции магнитного поля \(\overrightarrow{B}\).
Если вектор индукции магнитного поля \(\overrightarrow{B}\) перпендикулярен площади контура, то магнитный поток равен Ф = BS cos 90° = BS.
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока: \(\varepsilon_{i} = - \frac{\mathrm{\Delta}Ф}{\mathrm{\Delta}t}\), где:
εi ― ЭДС электромагнитной индукции, [B];
\(\frac{\mathrm{\Delta}Ф}{\mathrm{\Delta}t}\) ― скорость изменения магнитного потока, [Вб/с];
∆Ф ― изменение магнитного потока, [Вб];
∆t ― время, за которое происходит это изменение, [c].
В пределе, при ∆t → 0 ЭДС индукции равна производной магнитного потока по времени:
\(\varepsilon_{i} = - \frac{\mathrm{\Delta}Ф}{\mathrm{\Delta}t} = - Ф'(t)\), где:
εi ― ЭДС электромагнитной индукции, [B];
Ф’t ― производная магнитного потока по времени, [Вб/с].
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобочках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
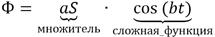
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что \(\varepsilon_{i} = - Ф'(t)\).
Подставив сюда значение производной, получим \(\varepsilon_{i}\)= abS · sin (bt).
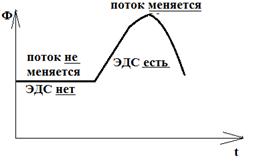
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет меняться и ЭДС не возникает.
Либо так, тогда будет меняться поток и возникать ЭДС:
Как видно из формулы магнитного потока Ф = BS cosα, изменение магнитного потока может быть вызвано разными факторами:
-
Увеличением или уменьшением модуля индукции магнитного поля (соответственно, величины \(\frac{\mathrm{\Delta}B}{\mathrm{\Delta}t}\));
-
Изменением направления вектора магнитного поля (т. е. изменением угла α);
-
Деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины \(\frac{\mathrm{\Delta}S}{\mathrm{\Delta}t}\));
-
Изменением нескольких из этих величин одновременно.
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Самоиндукция
При изменении тока через катушку в ней возникает ЭДС самоиндукции, которое будет мешать протеканию тока : \(\varepsilon_{i} = - L\frac{\mathrm{\Delta}I}{\mathrm{\Delta}t}\), где:
\(\varepsilon\) — ЭДС [В];
\(L\) — индуктивность [Гн];
\(\mathrm{\Delta}I\) — изменение тока [А];
\(\mathrm{\Delta}t\) — время изменения тока [с];
ЭДС самоиндукции, так же как и обычное ЭДС — это производная\(\text{\ ε}_{i} = - LI'\), где
\(\varepsilon\) — ЭДС самоиндукции [В];
\(L\) — индуктивность [Гн];
\(I\) — производная тока [А/с].
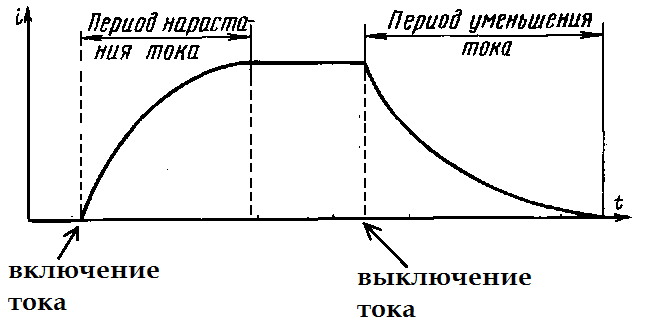
ЭДС самоиндукции приводит к тому, что при подключении цепи с катушкой к источнику тока, сила тока в цепи нарастает постепенно, а не сразу принимает постоянное значение – из-за того, что в момент включения в цепи возникают индукционные токи, стремящиеся уменьшить общий ток в цепи.
При отключении цепи с катушкой от источника тока, ЭДС самоиндукции наоборот приводит к тому, что ток в цепи медленно затухает, а не исчезает сразу – из-за наличия индукционных токов.
