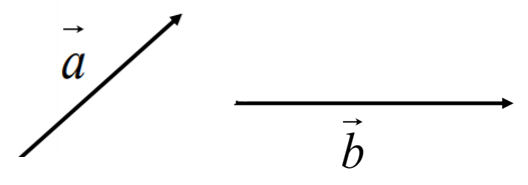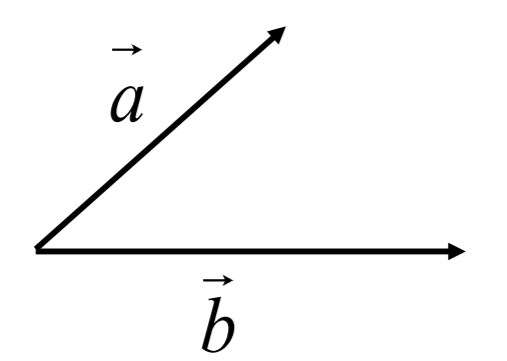Законы Ньютона
В физике огромную роль играют векторные величины, то есть величины, имеющие помимо величины еще и направление, среди них: импульс, сила, напряженность электрического поля, индукция магнитного поля и многие другие.
Со всеми этими векторными величинами нужно уметь выполнять математические действия, на которых будет строиться решение задач.
Операции с векторами
Для векторных величин существуют правила их сложения и вычитания. Необходимо понимать, что вектор это не обычное число, вектор имеет не только значение, но и направление, это накладывает некоторые особенности работы с ними.
Правило параллелограмма
Для того чтобы сложить два вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\) (рис. 1.1) нужно переместить их параллельно самим себе так, чтобы начала векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\ \)находились в одной точке (рис. 1.2). Затем достроить параллелограмм, сторонами которого будут эти вектора (рис. 1.3). Тогда суммой \(\overrightarrow{a} + \overrightarrow{b}\) будет вектор \(\overrightarrow{c}\), начало которого совпадает с общим началом векторов, а конец — с противоположной вершиной параллелограмма (рис. 1.4).
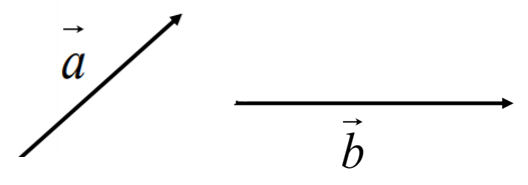
Рис. 1
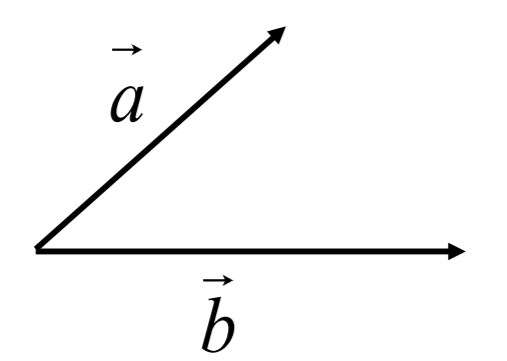
Рис. 1.2
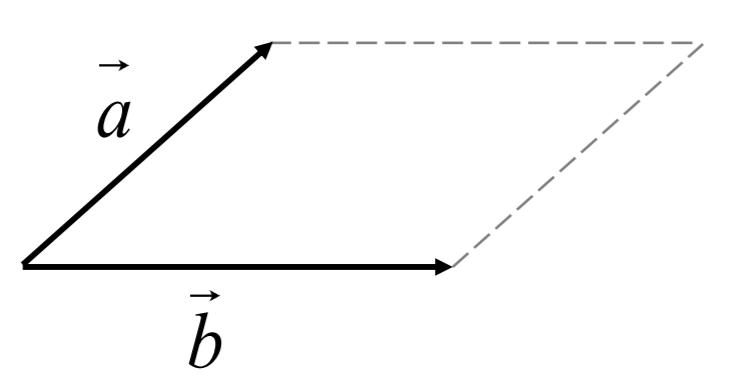
Рис. 1.3
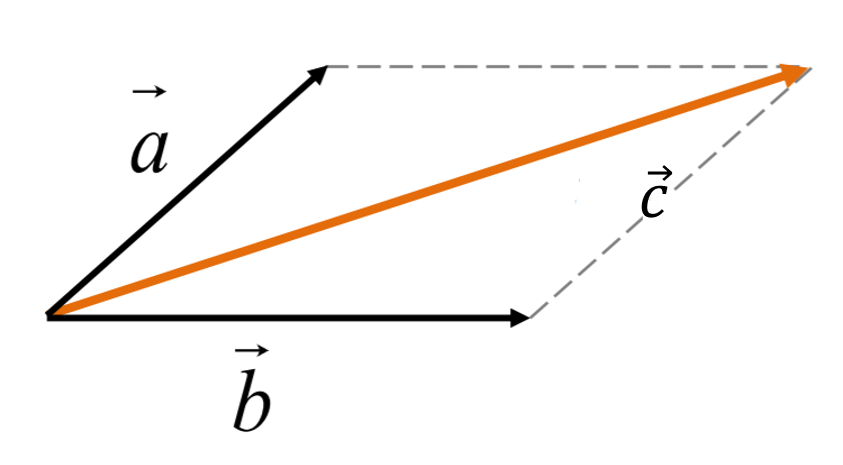
Рис. 1.4
Аналогично можно сложить два параллельных вектора \(\overrightarrow{a}\) и \(\overrightarrow{b}\) (рис. 2.1) и \(\overrightarrow{a}\) и \(\overrightarrow{d}\) (рис. 2.3). Суммы этих векторов \(\overrightarrow{c} = \overrightarrow{a} + \overrightarrow{b}\) и \(\overrightarrow{f} = \overrightarrow{a} + \overrightarrow{d}\) изображены на рис. 2.2 и 2.4. Причем, модули векторов c = a + b и f = |a − d|.
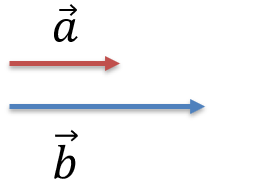
Рис. 2.1
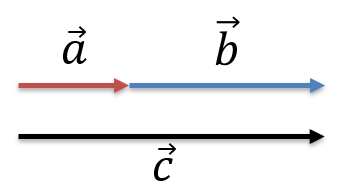
Рис. 2.2
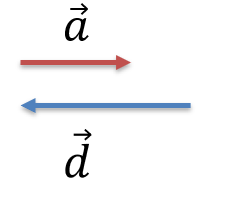
Рис. 2.3
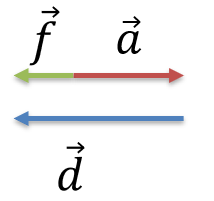
Рис. 2.4
Проекции векторов
В процессе решения задач, нам так же необходимо будет выбирать системы координат, относительно которых будет решаться уравнение. Большое значение для координатного представления векторов имеет понятие проекции вектора на ось.
Проекцией AB называется длина отрезка, образованного проекциями точек начала и конца вектора на заданную прямую (рис.3), причём проекции приписывается знак плюс, если направление проекции соответствует направлению оси, иначе — знак минус.
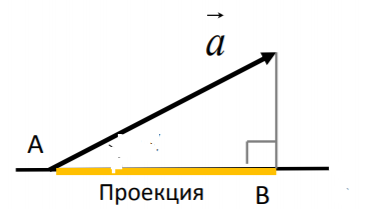
Рис.3
В задачах нам придется искать проекции векторов на оси х и у. Обычно проекция исходного вектора на ось х ищется через косинус угла между вектором и осью (рис.4).
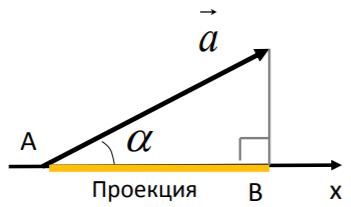
Рис. 4
AB = a ∙ cosα (из определения косинуса).
Аналогично, но уже при помощи синуса, ищутся проекции на ось y (рис.5).
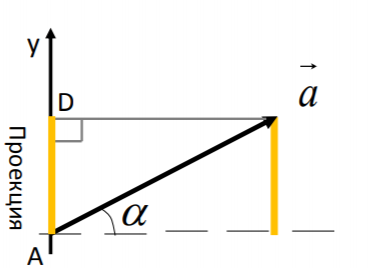
Рис.5
AB = a ∙ sinα (из определения синуса).
Законы Ньютона
I закон Ньютона: существуют такие системы отсчета, называемые инерциальными, в которых тело покоится или движется равномерно только до тех пор, пока на это тело не действуют никакие силы.
Инерциальные системы отсчета (ИСО) ― системы отсчета, связанные с телами, которые покоятся, или двигаются прямолинейно и без ускорения.
II Закон Ньютона: в ИСО \(\sum_{}^{}\overrightarrow{F} = m\overrightarrow{a}\) (векторная сумма всех сил равна произведению массы на ускорение), где ΣF ― векторная сумма сил (Н), m ― масса (кг), а ― ускорение (м/с2).
Сумма всех сил (ΣF) носит название равнодействующей силы. Ускорение тела всегда направленна в ту сторону, куда направленна результирующая сила.
III Закон Ньютона: Тела действуют друг на друга с силами равными по величине и противоположными по направлению.
В системе отсчета, движущейся с ускорением, на тело действует сила, направленная в сторону, противоположную ускорению.