Призмы. Основы

Призмы. Основы

Если мы не можем покрутить в руках треугольник (мы можем только изобразить его на плоскости), то мы можем покрутить в руках любую объёмную фигуру, например призму или пирамиду. Такие объемные фигуры называются геометрическими телами.

И наоборот, из-за того, что объемные фигуры не плоские, возникают сложности с их изображением на плоской бумаге, например, для построения чертежа. Поэтому, чтобы показать, что некоторые линии в многограннике невидимые, потому что находятся за другими его частями, их обозначают пунктиром.

Например:

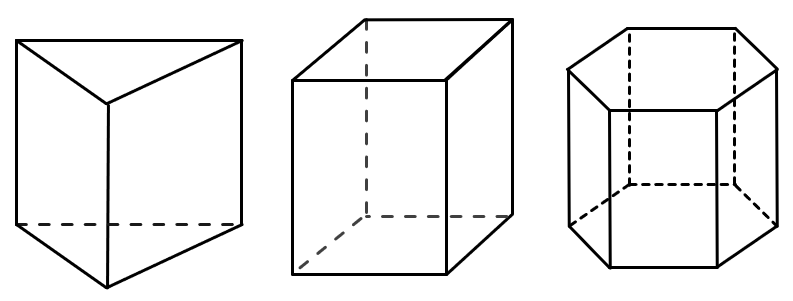
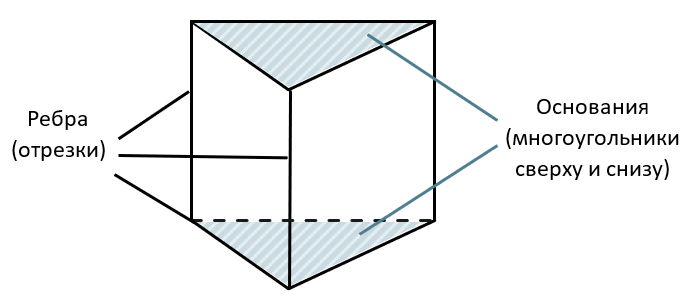
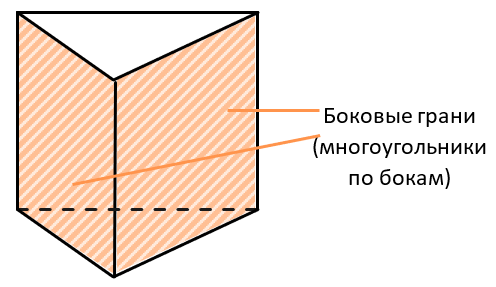
Призму можно узнать по двум одинаковым многоугольникам, которые находятся друг над другом, а их вершины попарно соединены ребрами. Эти многоугольники называются основаниями, а многоугольники, образованными ребрами призмы – боковыми гранями:

Призму называют по её основанию. В данном случае в основании призмы лежит треугольник, значит эта призма треугольная.

РАЗВЕРТКА ПРИЗМЫ

Для каждой объемной фигуры существует развертка. Развертка получается, если мысленно разрезать многогранник по его ребру и развернуть получившуюся фигуру на плоскости. Можно обратно получить многогранник из развертки: вырезать развертку и склеить её по ребру разрыва, тогда мы получим исходный многогранник

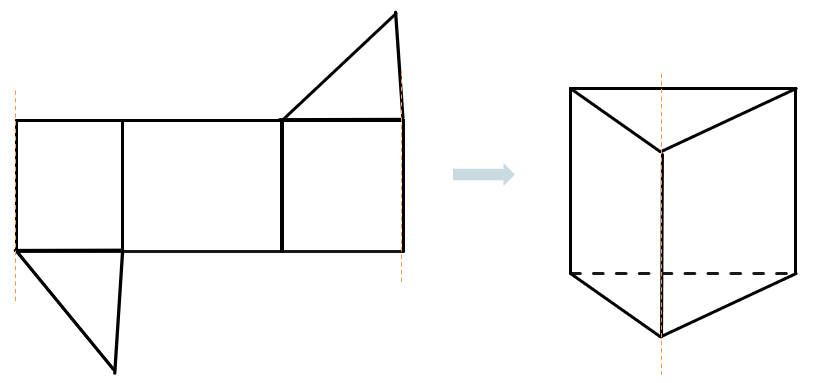
Например, развертка треугольной призмы выглядит так:

ПАРАЛЛЕЛЕПИПЕД И КУБ

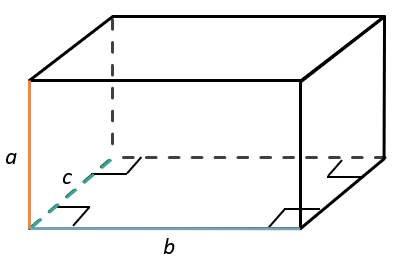
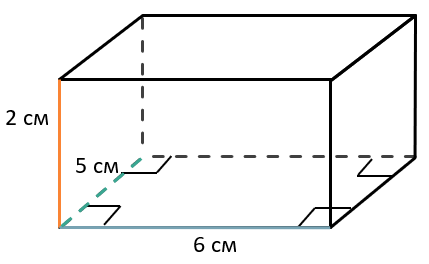
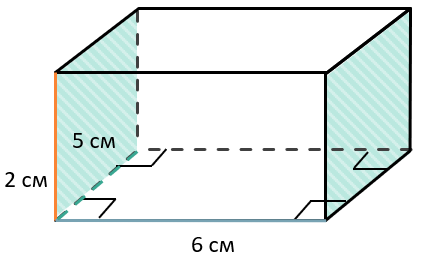
Найдите площадь поверхности (сумму площадей всех его граней) параллелепипеда, если его стороны равны 2 см, 5 см и 6 см.

1. У параллелепипеда есть три пары одинаковых граней, каждая из которых является прямоугольником:

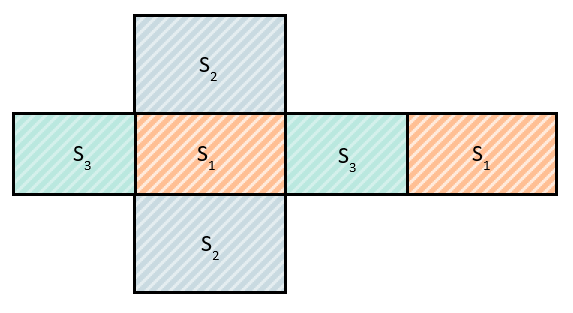
Это же будет видно и на развертке параллелепипеда:

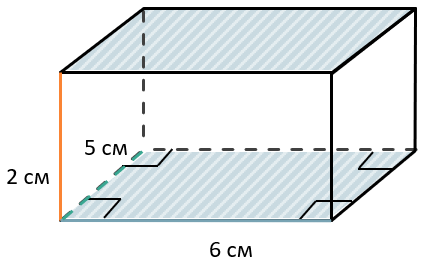
Площадь первой грани будет равна:

$S_{1} = 2\ см \bullet 6\ см = 12\ {см}^{2}$

2. Граней с такой площадью две, значит умножим её на два:

$12\ {см}^{2} \bullet 2 = 24\ {см}^{2}$

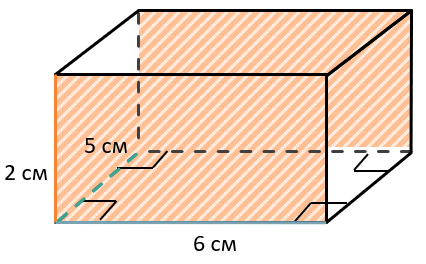
3. Так же найдем площади следующих двух одинаковых граней:

$S_{2} = 5\ см \bullet 6\ см = 30\ {см}^{2}$

$30\ {см}^{2} \bullet 2 = 60\ {см}^{2}$

4. И так же найдем площадь остальных граней:

$S_{3} = 2\ см \bullet 5\ см = 10\ {см}^{2}$

$10\ {см}^{2} \bullet 2 = 20\ {см}^{2}$

5. Сложим площади всех граней параллелепипеда и получим площадь его поверхности:

$24\ {см}^{2} + 60\ {см}^{2} + 20\ {см}^{2} = 104\ {см}^{2}$

Ответ: 104 ${см}^{2}$.

Объем параллелепипеда равен произведению его длины, ширины и высоты.

$V = abc$

Это то же самое, что умножить площадь основания параллелепипеда на его высоту (то есть боковое ребро):

$V = a \bullet (bc) = a \bullet S_{осн}$

По такой же аналогии можно находить объём любой прямой призмы. Нужно перемножить площадь её основания на боковое ребро (его высоту).

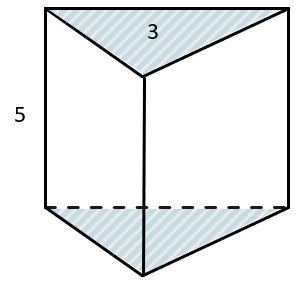
Найдите объем призмы с площадью основания равным 3 см2, и высотой, равной 5 см.

$V = a \bullet S_{осн} = 5\ см \bullet 3\ {см}^{2} = 15\ {см}^{3}$

Ответ: 15 ${см}^{3}$.

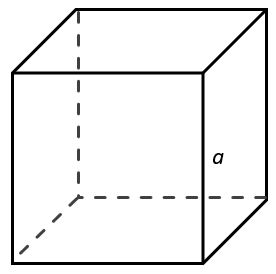
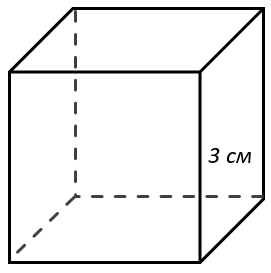
Найдите площадь поверхности и объем куба со стороной равной 3 см.

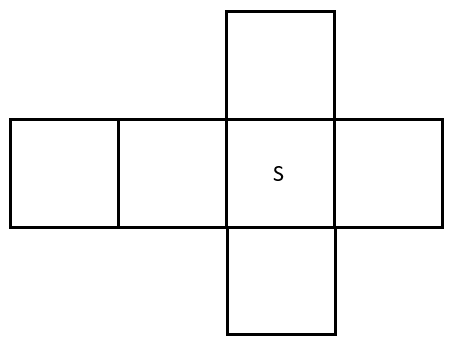
1. Найдем площадь поверхности куба. Все его стороны равны, а значит грани тоже равны между собой:

Значит у куба есть 6 одинаковых граней, площадь каждой из которых равна:

$S = 3\ см \bullet 3\ см = 9{\ см}^{2}$

$9\ {см}^{2} \bullet 6 = 54\ {см}^{2}$

2. Объём куба также равен произведению площади его грани на высоту, но высотой куба является его же сторон:

$V = S_{осн} \bullet a = 9\ {см}^{2} \bullet 3\ см = 27\ {см}^{3}$

Ответ: 54 ${см}^{2}$; 27 ${см}^{3}$.

Таким образом объем куба равен кубу его стороны:

$V_{куба} = a^{3}$

где a – сторона куба.