Тела вращения. Основы
Тела вращения. Основы
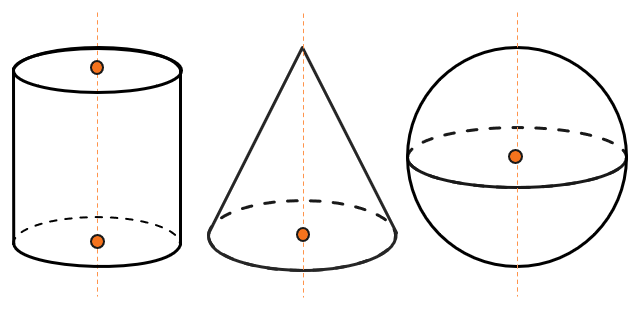
У каждого тела вращения есть оси, относительно которых они симметричны. Рассмотрим три тела вращения подробнее: цилиндр, конус и шар.
ЦИЛИНДР
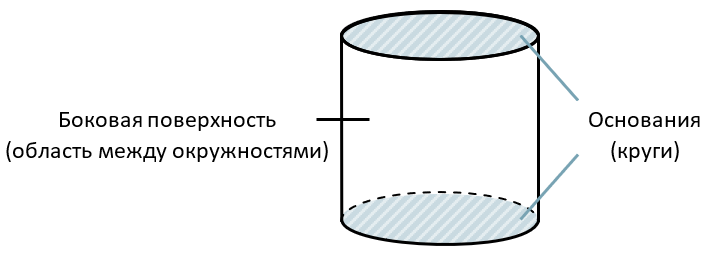
Цилиндр – это фигура, похожая на призму, с разницей лишь в том, что у нее в основаниях вместо многоугольников – окружность. Получается, что у такой фигуры нет боковых граней в виде многоугольников, а есть только она сплошная грань:
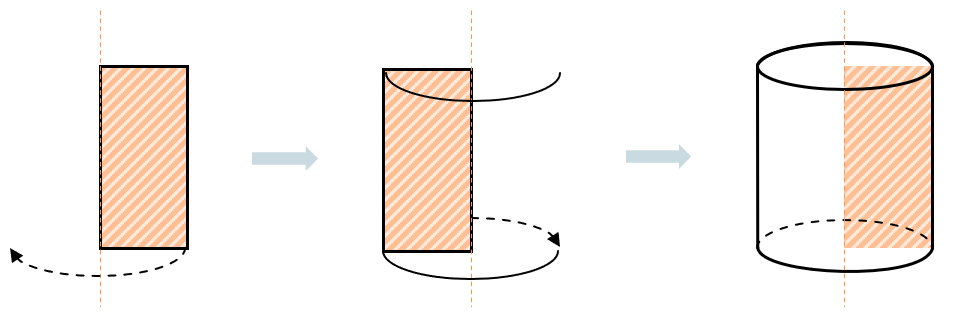
Цилиндр можно «образовать», если прокрутить прямоугольник вокруг одной из его сторон. Эта сторона прямоугольника станет осью будущего цилиндра:
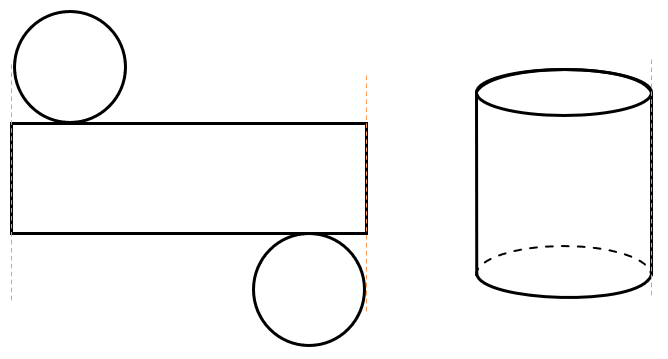
Разверткой цилиндра является прямоугольник (боковая поверхность цилиндра) и две окружности (его основания):
КОНУС
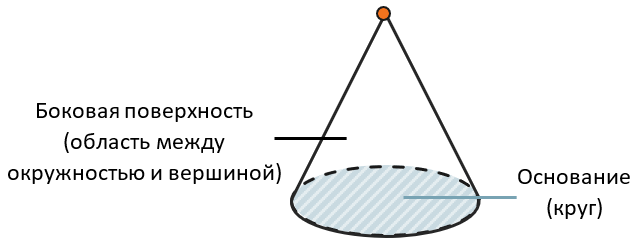
Конус – это тело вращения, похожее на пирамиду. У него есть основание и вершина, только вместо многоугольника в основании окружность, поэтому у нее тоже одна боковая грань:
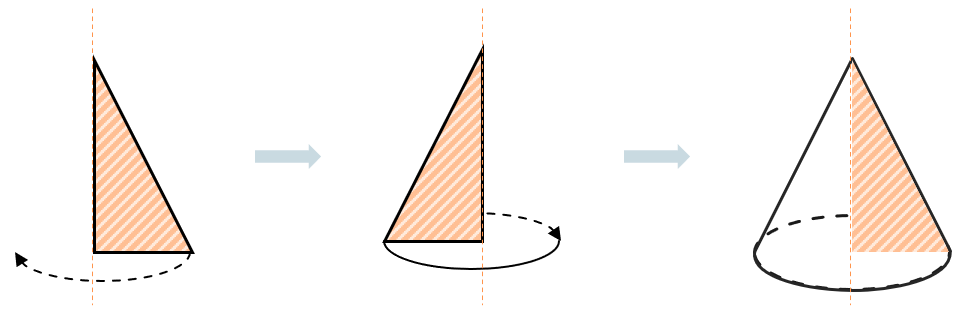
Конус можно «образовать» вращением прямоугольного треугольника вокруг его стороны, которая станет осью для будущего конуса:
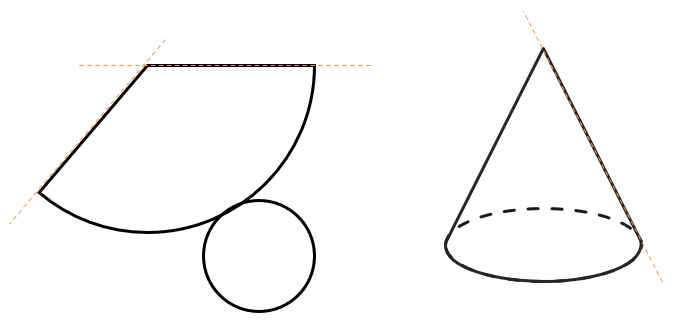
Развертка конуса – это часть большой окружности (боковая поверхность) и окружность поменьше (основание конуса):
ШАР
Шар – это фигура, которая абсолютная симметричная своей точке – центру.
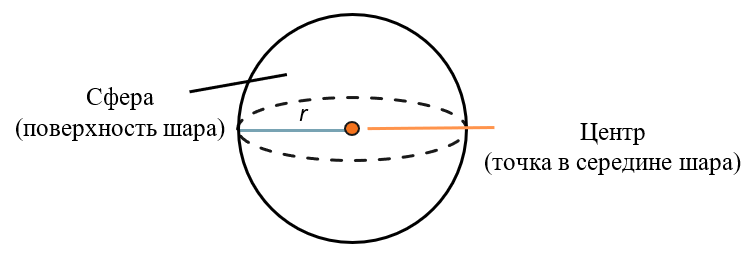
Шар выглядит как мяч или капля воды в воздухе. У шара нет оснований и граней. У него есть только сфера – поверхность шара. Любая точка на сфере удалена от центра шара на радиус \(r.\)
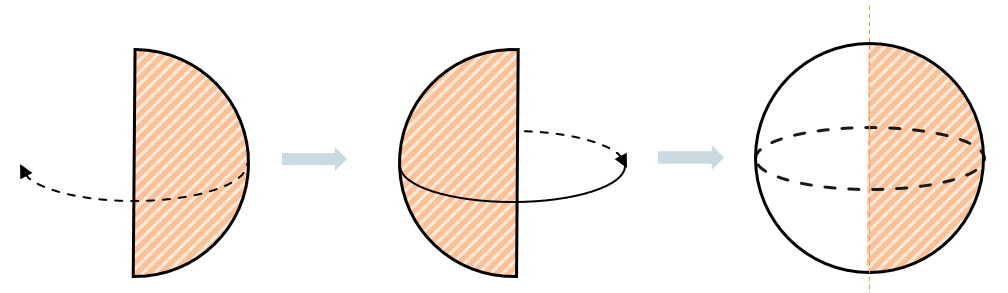
Сфера образована вращением полукруга около диаметра. Диаметр этой окружности становится осью шара:
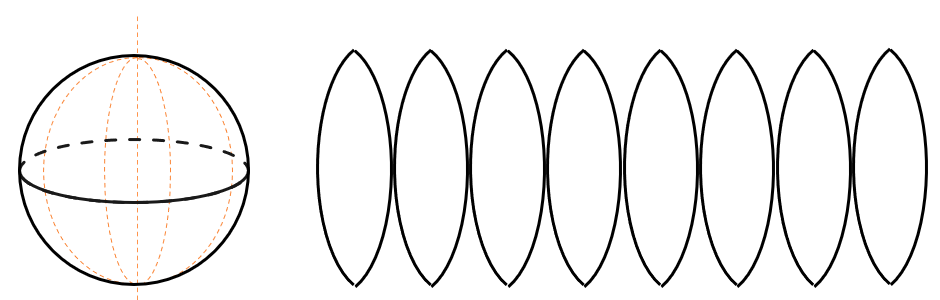
Развертка шара сложнее, чем у других геометрических тел, потому что у шара совсем нет плоских частей, например оснований. Можно представить развертку шара как перенос изображения нашей планеты с объемного глобуса на плоскую карту. Для этого используют меридианы на глобусе. Если мысленно «разрезать» глобус по каждому меридиану и развернуть его, то мы получим плоскую карту. Так и получают разверту любого шара:

Содержание