Обыкновенные дроби и действия с ними

Обыкновенные дроби и действия с ними

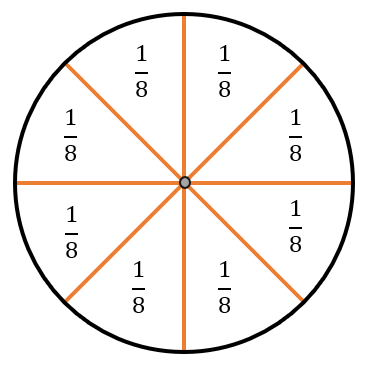
Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби$\ = \frac{1}{8}$.

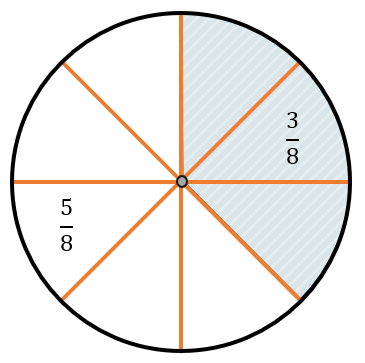
Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые$\ –\ \frac{3}{8}\$пирога и оставили пять восьмых $–\ \frac{5}{8}.$

Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида $\frac{5}{8}$ – обыкновенной дробью.

Дробь $\frac{1}{2}$ называется половиной, $\frac{1}{3}$ – третью, а $\frac{1}{4}$ – четвертью.

ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:

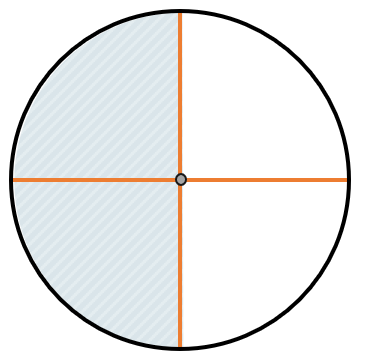
Если мы представим пирог, который разделили на четыре части и забрали две из них ($\frac{2}{4}$), мы увидим, что забрали ровно половину пирога, то есть $\frac{1}{2}$.

Значит $\frac{2}{4} = \frac{1}{2}$. Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.

Например:

$\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}$

$\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}$

$\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}$

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:

1. Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.

$\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}$

Например:

$\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}$

$\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}$

2. Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь $\frac{5}{6}\$к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на $42 : 6 = 7$, значит и числительно тоже нужно умножить на 7:

$\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}$

Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.

Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.

АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:

1. Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.
2. Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.
3. Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.
4. Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.

Например:

$\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}$

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:

1. Обратные числа:

Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:

$\frac{a}{1} = a : 1 = a$

Например: $\frac{4}{1} = 4$, $\frac{27}{1} = 27$.

Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа $\frac{4}{11}$ и $\frac{11}{4}$ или $19$ и $\frac{1}{19}$ – обратные друг другу.

2. Умножение дробей:

Представим умножение дроби на число как сумму дробей:

$\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}$

Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:

$\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}$

3. Деление дробей:

Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.

Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:

$\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}$

Таким же образом делят дроби на дроби:

$\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}$