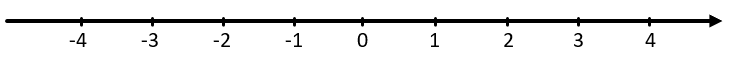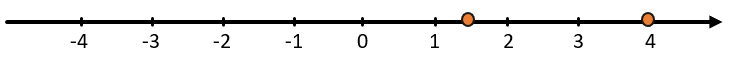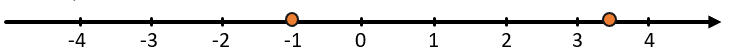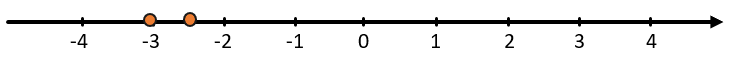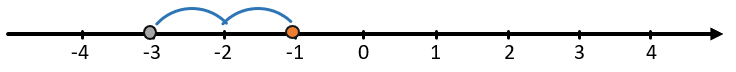Рациональные числа и действия с ними

Рациональные числа и действия с ними

Они могут быть как положительными, так и отрицательными.

Целые и дробные числа вместе образуют множество рациональных.

1. Любое целое число является рациональным, потому что его можно записать в виде $\frac{m}{1}$.

Например:

$–4 = \frac{- 4}{1}$

$2 = \frac{2}{1}$

$0 = \frac{0}{1}$

2. Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.
3. Любое рациональное число можно записать в виде десятичной или периодической дроби.

Например:

$\frac{1}{3} = 0,33333333..$

Повторяющиеся цифры периодической дроби записывают в скобках, например:

$\frac{1}{3} = 0,(3)$

$\frac{5}{11} = 0,45454545 = 0,(45)$

СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение:

1. Переместительное свойство:

$a + b = b + a$

2. Сочетательное свойство:

$a + (b + c) = (a + b) + c = (a + c) + b = a + b + c$

3. Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:

$a + 0 = a$

$a + ( - a) = 0$

Умножение:

1. Переместительное свойство:

$ab = ba$

2. Сочетательное свойство:

$a(bc) = (ab)c = (ac)b = abc$

3. Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:

$a \bullet 1 = a$

$a \bullet \frac{1}{a} = 1$

4. Если один из множителей равен нулю, то и всё произведение равно 0:

$a \bullet 0 = 0$

$0 \bullet b = 0$

$0 \bullet 0 = 0$

5. Распределительное свойство:

$(a + b)c = ac + сb$

ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ

Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел. Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.

СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:

Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.

Например:

1. Сравним числа 1,5 и 4:

Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.

$4 > 1,5$

2. Сравним числа 3,5 и -1:

Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.

$3,5 > - 1$

3. Сравним числа -2,5 и -3:

Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.

$- 2,5 > - 3$

СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).

Например:

1. Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:

Видим, что $1 + 2,5 = 3,5$.

Сумма положительных чисел – положительное число.

2. Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.

Получилось, что $- 1 + ( - 2) = - 3.$

Сумма отрицательных чисел – отрицательное число.

3. Найдем разность положительных чисел 4 – 1,5. Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:

Получилось, что $4\ –1,5 = 2,5.$

Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.

4. Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:

Получим, что $2–4 = - 2.$

Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.

5. Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:

Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.

6. Найдем сумму двух противоположных чисел 3 + (-3). От координаты 3 пройдем 3 отрезка в отрицательном направлении:

Видим, что $3 + ( - 3) = 0.$

Сумма двух противоположных чисел $\mathbf{= 0.}$

УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

1. Рациональные числа умножаются и делятся не смотря на знак.
2. Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.

Например:

$3 \bullet 4 = 12$

$- 6 \bullet ( - \frac{1}{2}) = 3$

$7:( - 2) = - 3,5$

$- 12:\frac{1}{3} = - 12 \bullet 3 = - 36$