Движение по окружности. Гравитация
Движение по окружности
Период — время, за которое тело делает полный оборот по окружности.
Частота — равна количеству оборотов по окружности, совершенных за единицу времени.
, где
v ― частота [Гц],
t ― время [c],
N ― количество оборотов.
T – период вращения тела
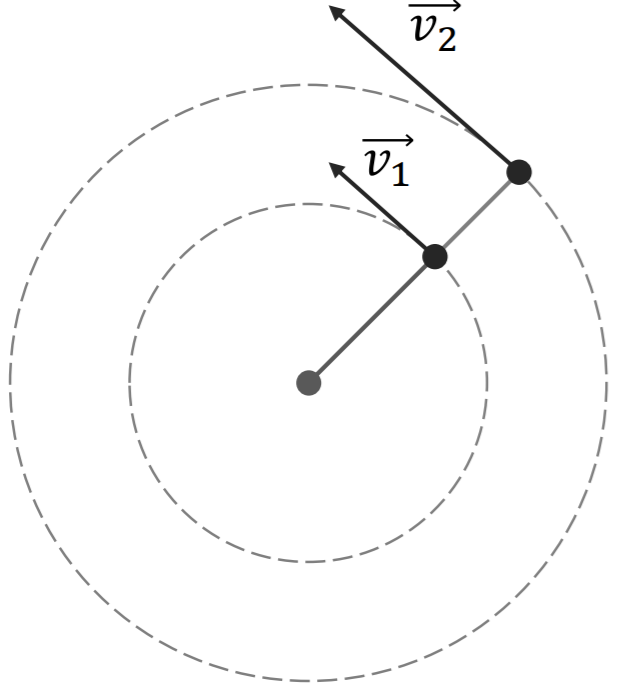
При движении по окружности часто удобно использовать не обычную скорость, а угловую скорость.
Угловая скорость численно равна углу поворота радиуса за единицу времени.
, где
∆φ ― угол поворота [рад],
∆t ― промежуток времени [с],
ω ― угловая скорость .
Линейную скорость точки на определенном расстоянии (радиусе) R от оси вращения можно считать как:
v = ωR.
Соответственно, чем больше будет радиус окружности, тем больше будет линейная скорость, при постоянной угловой скорости.
Таким образом, период может быть выражен как отношение длины описываемой окружности к линейной скорости
, где
T ― период [с],
R ― радиус окружности [м],
v ― скорость [м/с].
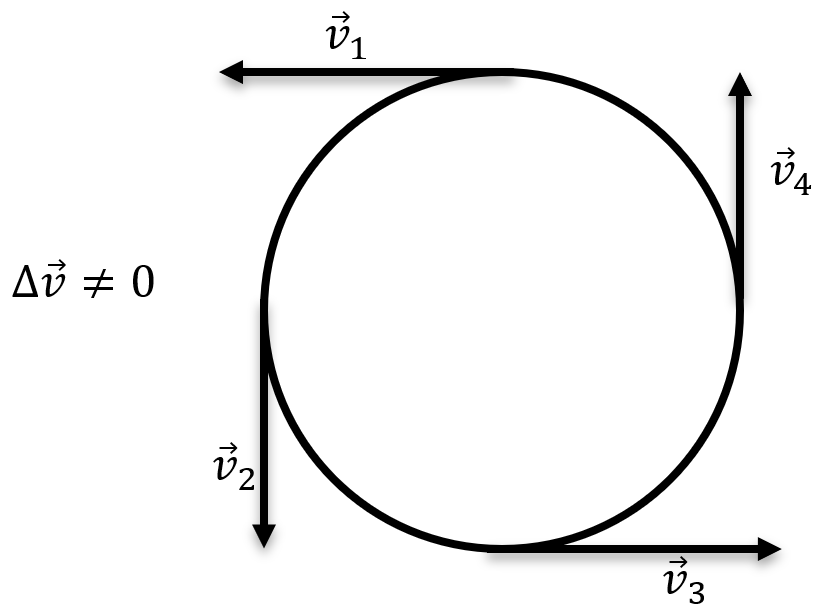
При движении по окружности тело в каждый момент времени меняет направление своей скорости, а, значит, двигается с ускорением.
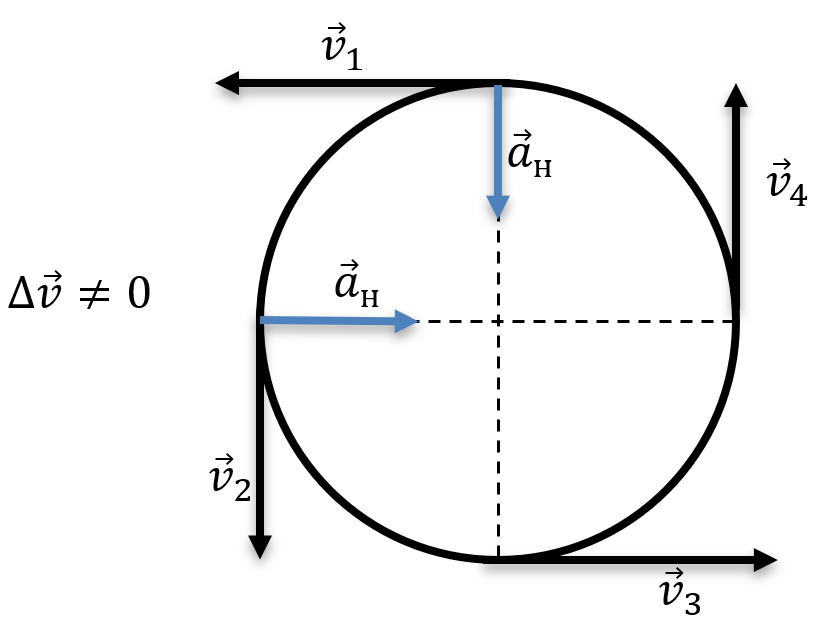
Ускорение, которое испытывает тело, движущееся по окружности, называется нормальным или центростремительным и всегда направленно к центру окружности.
Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой :
, где
R ― радиус окружности [м],
an ― нормальное ускорение [м/с2],
v ― скорость [м/с],
ω ― угловая скорость .
Закон всемирного тяготения:
m1, m2 – массы тел [кг]
R – расстояние между двумя телами [м]
G – гравитационная постоянная, 6,7 ⋅ 10–11 [Н⋅м2 /кг2 ]
Содержание