Геометрическая оптика. Линзы
Насколько ты готов к ОГЭ?
Проверь себя и разбери результаты с экспертом
пройти тест

Линзы
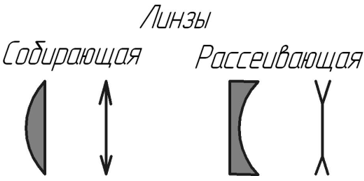
Линзы бывают собирающими и рассеивающими. Собирающая линза собирает падающие на нее лучи в одной точке (фокусе), а рассеивающая разводит лучи в разные стороны. В большинстве случаев линза является собирающей, если ее середина толще краев, и рассеивающей ― если края толще середины линзы.
Тонкая линза ― это линза, толщиной которой можно пренебречь, и для удобства расчетов она принята равной нулю.
Условные обозначения линз:
Далее под «линзами» для краткости будем понимать собирающие тонкие линзы.
Основные элементы линзы
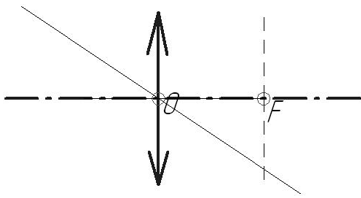
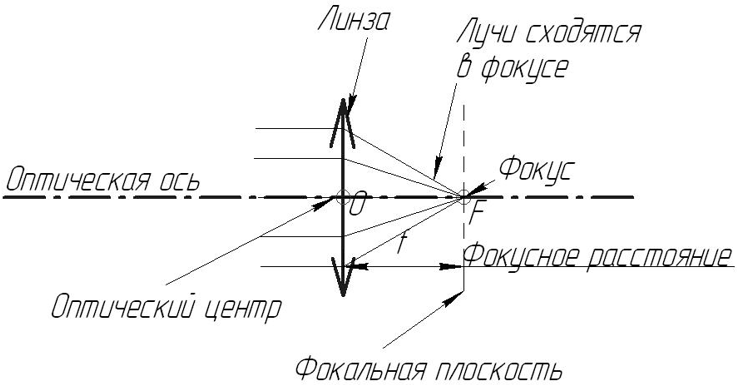
Оптическая ось (главная оптическая ось) ― прямая, проходящая через центры изогнутых поверхностей линзы, для симметричных линз ― просто через центр линзы.
Оптический центр ― точка в центре линзы, лежащая на ее оптической оси.
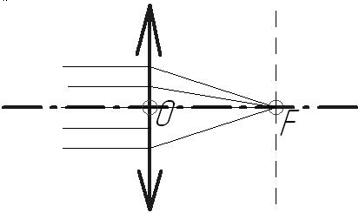
Фокус линзы ― точка, в которой собираются все лучи, идущие параллельно главной оптической оси.
Фокусное расстояние (F) ― расстояние от оптического центра линзы до ее фокуса.
Фокальная плоскость ― плоскость, проходящая через фокус линзы и перпендикулярная оптической оси.
Двойной фокус (2F) ― это точка, находящаяся на оптической оси линзы на расстоянии двух фокусных расстояний от оптического центра линзы.
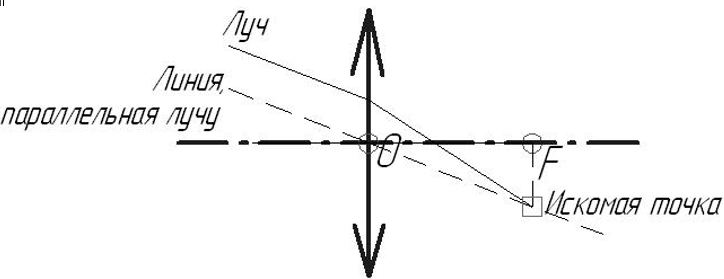
Построение изображения, полученного с помощью линзы, основывается на следующих правилах:
Чтобы найти эту точку нужно построить вспомогательную линию, параллельную этому лучу и проходящую через оптический центр линзы и найти пересечение этой линии с фокальной плоскостью ― т. е. перпендикуляром, опущенным или поднятым к этой линии из фокуса линзы.
Изображение в зависимости от положения относительно линзы
Лучи идут из источника света в его изображение по всем траекториям.
Мнимое изображение ― изображение, полученное при пересечении продолжения лучей.
При мнимом изображении расстояние до предмета b ― отрицательная величина.
Изображения, полученные с помощью собирающей линзы, получаются различными, в зависимости от того, на каком расстоянии от линзы расположен оригинал. С помощью линз можно получать увеличенные и уменьшенные изображения, изображения прямые и перевернутые относительно оригинала, действительные и мнимые изображения.
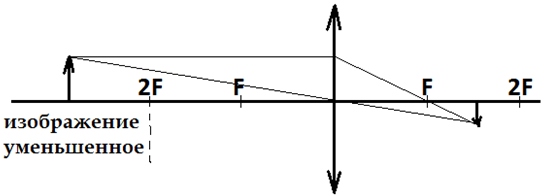
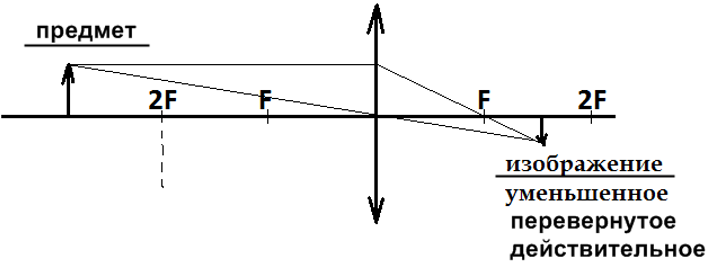
Предмет расположен за двойным фокусом линзы. Пример построения изображения предмета в виде стрелки:
Свойства изображения: уменьшенное, перевернутое, действительное, расположено между фокусом и двойным фокусом линзы, по другую сторону линзы от предмета. Такое изображение создает объектив телескопа.
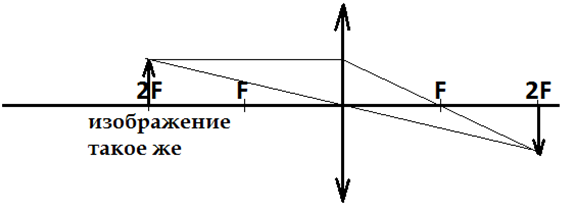
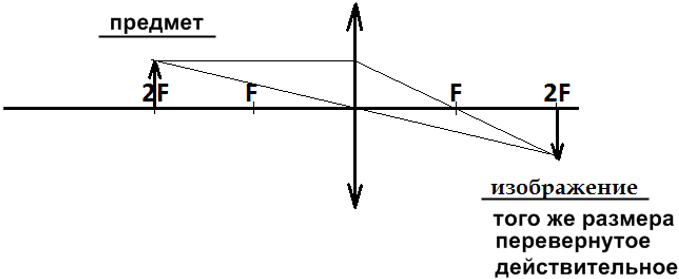
Предмет расположен в двойном фокусе. Пример построения изображения предмета в виде стрелки:
Свойства изображения: того же размера, что и сам предмет, перевернутое, действительное, расположено точно в двойном фокусе линзы, по другую сторону линзы от предмета.
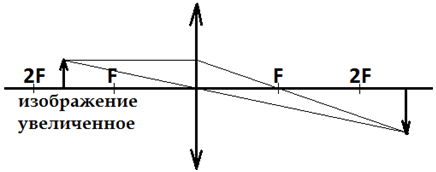
Предмет расположен между двойным фокусом и фокусом. Пример построения изображения предмета в виде стрелки:
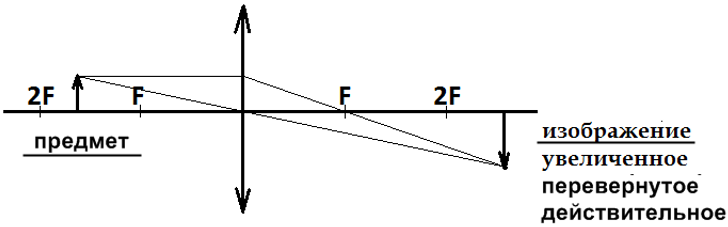
Свойства изображения: увеличенное, перевернутое, действительное, расположено за двойным фокусом линзы, по другую сторону линзы от предмета. Такое изображение создают окуляр телескопа, а также микроскопы.
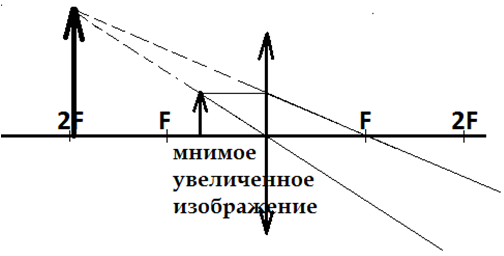
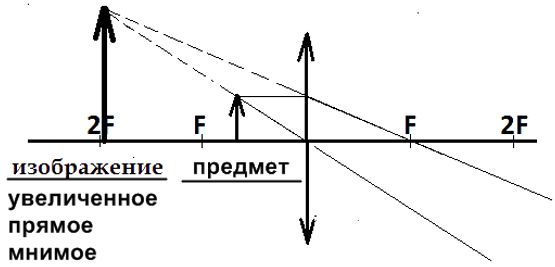
Предмет расположен между фокусом и оптическим центом линзы Пример построения изображения:
Свойства изображения: увеличенное, прямое, мнимое, расположено с той же стороны линзы, что и предмет.
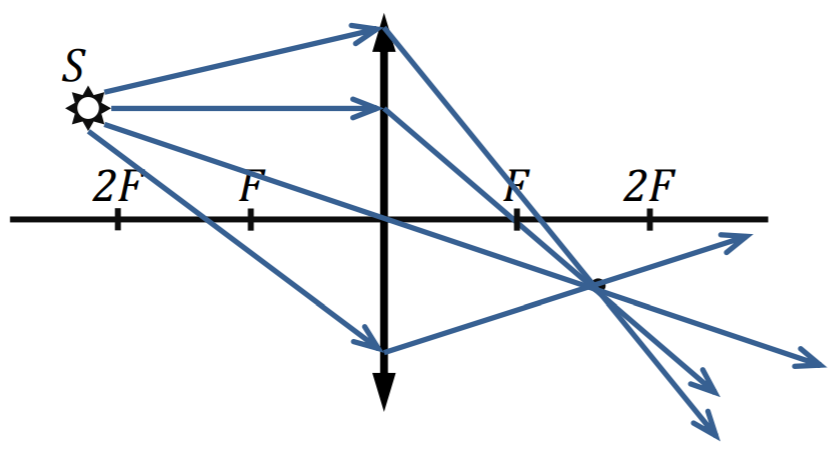
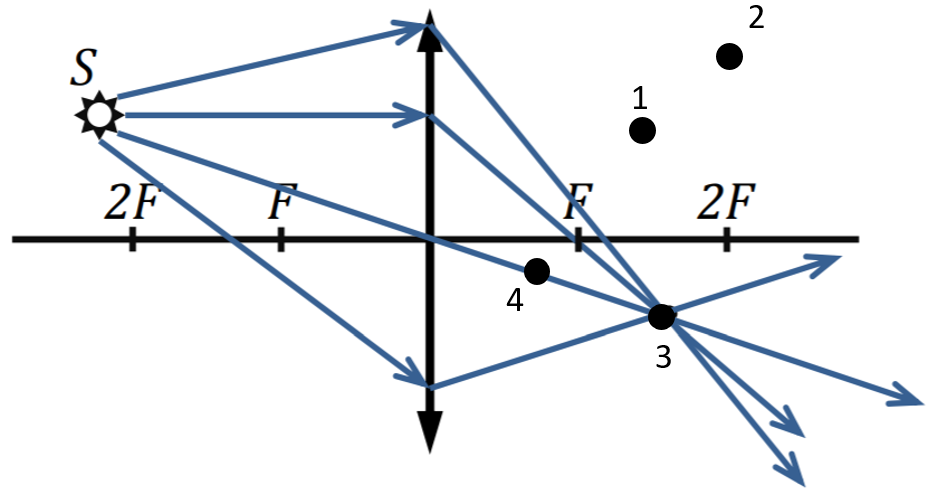
Лучи из источника света расходятся во все стороны. Преломляясь в линзе, все лучи сходятся в изображении источника света. На рисунке показаны лучи, выходящие из источника света S. Поскольку источник находится на расстоянии 2F от линзы ― то все лучи, преломившись в линзе, сходятся в его действительное изображение в точке 3.
Точки 1, 2 и 4 ― ошибочные решения для задачи, в которой нужно найти изображение источника. Точка 4 не подходит, так как расположена на расстоянии F, а не 2F от линзы. Точки 1 и 2 находятся не с той стороны от главной оптической оси линзы ― ведь при таком положении источника линза дает перевернутое изображение. В данном случае верно решение 3 ― изображение находится на расстоянии 2F и перевернутое.
Оптическая сила линзы ― величина, обратная фокусному расстоянию линзы
\(D = \frac{1}{F}\), где
D ― оптическая сила линзы [дптр];
F ― фокусное расстояние [м].
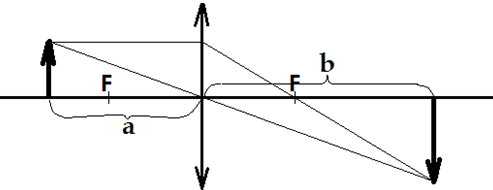
Формула тонкой линзы связывает расстояние от линзы до предмета, до изображения, и фокусное расстояние линзы
\(\frac{1}{a} + \frac{1}{b} = \frac{1}{F}\), где
a― расстояние до предмета [м];
b ― расстояние до изображения [м];
F ― фокусное расстояние [м]
Из формулы тонкой линзы легко определить любое из трех расстояний. Расстояние до предмета равно a = 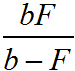
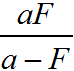
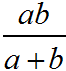
Фокусное расстояние линзы зависит не только от линзы, но и от показателя преломления среды, в которой находится линзе. Если линзу перенести из среды с меньшим показателем преломления n1 в среду с большим показателем преломленияn2, n2 ˃ n1 ― ее фокусное расстояние увеличится. Если перенести из среды с большим показателем n1 преломления в среду с меньшим n2, n2 ˂ n1 ― уменьшится.
Увеличение линзы \(Г = \frac{a}{b}\), где
Г ― увеличение линзы;
a― расстояние до предмета [м];
b ― расстояние до изображения [м].
Работа с рассеивающей линзой полностью аналогична работе с собирающей, но при работе с формулами нужно учитывать, что F < 0, b < 0, но a > 0, то есть в формулы собирающей линзы нужно подставлять переменные F и b со знаками минус.

Содержание