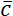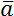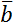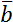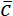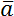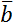Математика в физике. Физические величины.
Прежде всего необходимо ввести понятия, которыми мы будем оперировать дальше: «физическая величина» и «измерение физической величины».
Физическая величина: Число + Единица измерения
Измерить физическую величину – сравнить ее с величиной, принятой за единицу.
Единицы измерения могут быть разными. Карандаши, длины рук и пальцев (как измеряли расстояния раньше в России), но все это недостаточно объективные и точные величины, ведь длины карандашей и пальцев могут быть разные. По этой причине в физике была разработана и принята эталонная система мер для всех физических величин – система интернациональная (СИ).
В ней описаны основные физические величины и их единицы измерения:
Помимо основных, как мы сказали, базовых единиц, существуют также дополнительные – производные от основных.
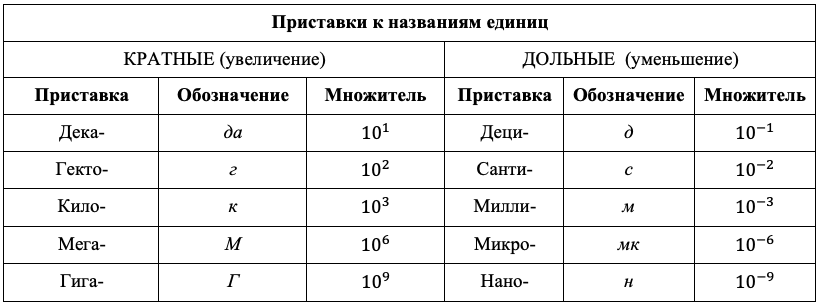
Зачастую в физике могут встречаться очень маленькие или очень большие числа. Переписывать нули каждого числа в уравнение неудобно, поэтому очень часто в физике для единиц измерения используют приставки – кратные (обозначающие увеличение, умножение на какое-то число) и дольные (обозначающие уменьшение, деление на какое-то число). Все приставки сведены в таблицу ниже.
Существуют еще внесистемные единицы, которые не используются в СИ, но часто применяются в быту, поэтому мы должны знать, как переводить их в СИ.
Внесистемные единицы:
1л = 1 дм3 = 10-3м3
1ч = 60 мин = 3,6∙103с
1 сутки = 24 = 8,64∙105с
Для проведения расчетов с числами, которые представлены через дольные или кратные приставки, эти приставки необходимо обязательно расписать и привести числа к размерности, указанной в СИ. Нам предстоит расписывать приставки через степени, которые они обозначают:
\(1,2\ кН = 1,2 \bullet 10^{3}\ Н\)
\(6\ км = 6 \bullet 10^{3}\ м\)
В случае, если обычную величину возводят в некоторую степень, ее приставка также возводится в эту степень. Далее остается лишь посчитать численное значение путем подстановки степени, которую значит приставка и свойства \({{(a}^{n})}^{m} = a^{n \bullet m}\):
\(3,2\ км^{2} = 3,2\ \bullet \left( 10^{3}\ м \right)^{2} = 3,2 \bullet 10^{6}\ м^{2}\)
\(5\ мм^{2} = 5 \bullet \left( 10^{- 3}\ м \right)^{2} = 5 \bullet 10^{- 6}\ м^{2}\)
Зачастую при расчетах придется переводить величины из несистемных в системные, как например «км/ч» в «м/с». Для удобства перевода воспользуемся знанием о кратных и дольных коэффициентах на нескольких примерах:
\(72\frac{км}{ч} = 72\frac{10^{3}\ м}{3,6 \bullet 10^{3}\ с} = \frac{72 \bullet 1}{3,6}\frac{м}{с} = 20\frac{м}{с}\)
\(12\frac{г}{{см}^{3}} = 12\frac{10^{- 3}\ кг}{{{(10}^{- 2}\ м)}^{3}} = \frac{12 \bullet 10^{- 3}}{10^{- 6}}\frac{кг}{м^{3}} = 12 \bullet 10^{- 3 + 6}\ \frac{кг}{м^{3}} = 12 \bullet 10^{3}\ \frac{кг}{м^{3}}\)
Последнее, о чем необходимо упомянуть в измерении размера малых объектов. Если измеряемая величина мала, то можно измерить эту величину у целого ряда объектов, после чего можно разделить получившееся значение на количество объектов.
Так, если нужно измерить ширину зернышка риса, можно выложить в ряд 100 таких зерен, замерить ширину ряда и получившееся число разделить на 100 (число объектов ряда). Аналогично с массой.
При этом стоит учитывать погрешность измерения, если объекты не идентичны друг другу и измерительные приборы не идеальны.
Погрешность – допускаемая при измерении неточность. Не может быть больше цены деления прибора (расстояния между ближайшими друг к другу отметками на шкале прибора). Чем меньше цена деления, тем точнее измерение.
При наличии погрешности в измерениях стоит записывать результат измерения как:
\(ФВ = a \pm \mathrm{\Delta}a\)
ФВ – физическая величина;
a – результат измерения;
∆a – цена деления прибора.
Математические формулы, необходимые в физике.
Ниже приведены формулы алгебры и геометрии, которые наиболее часто требуются для решения задач по физике.
Проценты:
Само слово «процент» происходит от английского «per cent», то есть «одна сотая доля». То есть если мы что-то рассматриваем как целое, – это всегда 100 процентов, сто частей, а один процент от целого – это одна часть из ста. Процент – это не что иное, как просто одна сотая от целого.
Одна сотая от 100 это 1. Одна сотая от 200 это 2.
Чтобы найти, сколько составляет 1 процент от числа N, нужно поделить это число на 100, то есть найти, чему равна одна часть из ста. Чтобы найти, сколько составляет не 1 процент, а, например, 20%, нужно умножить полученную одну сотую на 20, то есть взять 20 частей из 100.
Эти два действия можно сократить в одно, умножив на соответствующую десятичную дробь.
Например, если нам нужно найти 15% от 200, мы должны поделить на 100 и умножить на 15: \(\frac{200 \bullet 15}{100}\)
Мы получим то же самое, если умножим на 0,15, ведь \(\frac{15}{100} = 0,15\).
Нахождение процента r % от числа N: \(\frac{N\ \bullet \ r}{100}\)
Пример: 15% от 200 = \(\frac{200 \bullet 15}{100} = 200 \bullet 0,15\)
В некоторых случаях вас могут просить найти не процент от числа, а определить, сколько процентов составляет одно число от другого. Например: сколько процентов составляет число А от числа Б? В таком случае нужно поделить число А на то число, от которого считаем процент – то есть на число Б. При этом получится некоторая дробь. Теперь, чтобы найти процент, нужно дробь умножить на 100%.
Есть другой способ понять взятие такого процента. Вернемся к вопросу: сколько процентов составляет число А от числа Б? Можно сначала найти, сколько вообще составляет 1% от числа Б, то есть поделить на 100: Б/100. Далее необходимо понять, сколько таких одних сотых частей от Б содержится в числе А. Чтобы понять, сколько процентов содержится в А, нужно А поделить на один процент от Б: \(\frac{А}{Б/100} = \frac{A}{Б} \bullet 100\)
Сколько процентов число А составляет от числа Б?: \(\frac{A}{Б} \bullet 100\%\)
1% от Б: \(\frac{Б}{100}\)
Сколько 1% от Б содержится в А: \(\frac{А}{Б/100} = \frac{A}{Б} \bullet 100\)
Если требуется найти, на сколько процентов отличаются друг от друга числа, аналогичными действиями можно прийти к следующим формулам:
На сколько процентов число А больше числа Б?
\(\frac{A - Б}{Б} \bullet 100\%\) ИЛИ \(\left( \frac{A}{Б} - \frac{Б}{Б} \right) \bullet 100\% = \left( \frac{A}{Б} - 1 \right) \bullet 100\% = \frac{А}{Б} \bullet 100\% - 100\%\)
В процентах всегда важно, от чего его считать.
Процент числа А от числа Б ≠ процент числа Б от числа А.
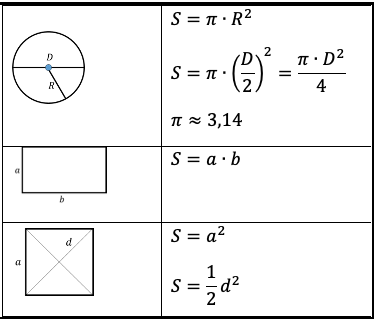
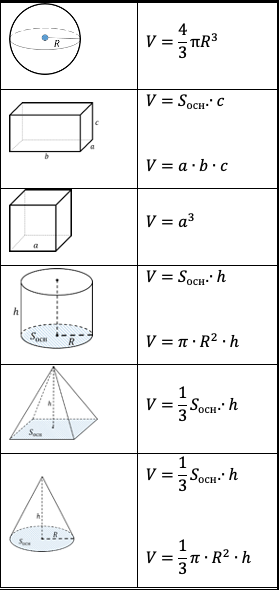
Формулы геометрии:
На данном этапе вам требуется знать формулы для нахождения только двух величин – площадей и объемов. Ниже представлены необходимые для этого формулы.
Площади плоских фигур:
Аналогичная схема потребуется для формул объема пространственных фигур:
Скалярные и векторные физические величины:
Физическая величина – это параметр, который количественно описывает физические тела и явления. Физические величины бывают разные – масса, время, скорость, сила, энергия и т.д. Но все эти величины можно разбить на два вида: скалярные и векторные.
Скалярные физические величины – это величины, которые имеют только одну характеристику: просто число, то есть численное значение. Векторные величины – это величины, которые имеют две характеристики: число, то есть модуль, и направление в пространстве.
Скалярные величины представляют собой просто число, либо положительное, либо отрицательное. С этими числами можно делать алгебраические действия: складывать, вычитать, умножать, делить - как с обычными числами. Скалярные величины обозначаются просто соответствующим символом без дополнительных пометок. Например, a.
Для описания векторных величин введем понятие вектора. Вектор – это направленный отрезок, для него задано, какой из его концов является началом, а какой – концом. Длина этого отрезка называется «модуль вектора» и является тем самым числом, с помощью которого численно характеризуется физическая величина, а направление вектора говорит о том, куда направлена величина. Векторные величины обозначаются соответствующим символом со стрелкой над ним. Модуль векторной величины обозначают либо символом модуля, либо просто убирают стрелку.
Получается, что векторные физические величины – величины, которые имеют две характеристики: модуль и направление в пространстве. Например, \(\overrightarrow{a}\), модуль: \(\left| \overrightarrow{a} \right|\), a.
Ниже приведена таблица с наиболее распространенными величинами в физике:
Операции с векторами:
Векторные величины нельзя складывать алгебраически, то есть суммировать их модули. Возможны ситуации, когда вектора направлены в одну сторону, в разные стороны, перпендикулярно друг другу. Для векторных величин всегда должно быть указано их направление.
Сложение векторов в физике делится на две формы – если вектора лежат на одной прямой и, если не лежат.
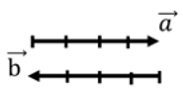
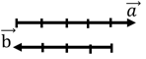
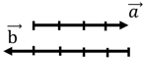
Начнем с первой формы. Представим себе два противоположно направленных вектора, которые нам необходимо сложить.
Если векторы равны по модулю, то есть их длины равны, то их сумма равна 0.
Если один из векторов больше другого по модулю, и тогда сумма векторов не будет равна 0. Сумма векторов будет направлена в ту сторону, куда направлен наибольший по модулю вектор.
На рисунке ниже сумма векторов равна 1 условной единице и направлена вправо.
Второй пример – сумма векторов равна все еще 1 условной единице, но направлена уже влево.
Получается, сумма векторов, направленных по одной прямой:
- в одну сторону, равна вектору, направленному в ту же сторону и имеющему модуль, равный сумме модулей исходных векторов.
- в разные стороны, равна вектору, направленному в сторону наибольшего по модулю вектора и имеющему модуль, равный разности модулей исходных векторов.
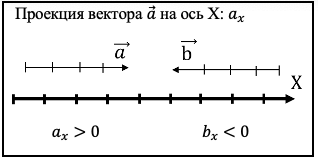
Чтобы избежать формулировок «сумма направлена влево/вправо» требуется ориентир, глядя на который мы бы могли сказать: это направление – положительное, пометим его знаком «+», а это – отрицательное, его пометим знаком «-». В качестве такого ориентира используют ось, которая направлена в определенную сторону и это направление принимают за положительное. Соответственно, направление, противоположное оси – за отрицательное. И для удобства работы с векторами можно ввести ось и продолжать работу не с изначальным вектором, а с его проекцией на ось. Если вектор проецируют на ось, то убирают верхнюю стрелочку и помечают вектор индексом. Если направления вектора и оси совпадают, то проекция будет иметь знак плюс, если противоположны – то минус.
Случай, когда вектор и ось направлены под некоторым углом друг к другу, требует знание тригонометрии и рассматривается уже в старших классах.
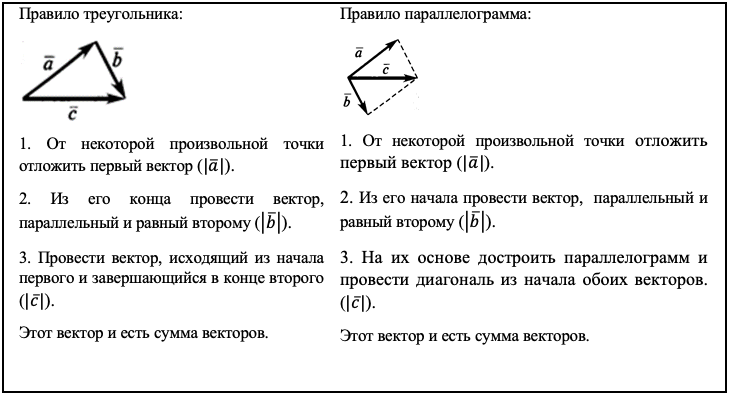
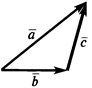
Во второй форме сложения векторов векторы уже не лежат на одной прямой. Для сложения векторов под углом можно применить одно из двух правил: правило треугольника или правило параллелограмма. Наглядный ход действий для каждого правила приведен ниже:
Последнее, о чем стоит упомянуть – разность векторов.
Разность двух векторов 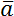
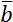
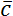
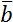
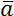
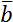
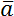
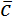
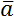
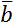
Вектор