Натуральные числа и действия с ними

Натуральные числа и действия с ними

Самое маленькое натуральное число (натурального ряда) – 1, самого большого числа нет, потому что натуральный ряд можно продолжать бесконечно.

КАК ЧИТАТЬ НАУТРАЛЬНЫЕ ЧИСЛА:

1. Значность натуральных чисел.

• Если натуральное число состоит из одной цифры – такое число однозначное (4, 8, 2, 7);
• Если натуральное число состоит из двух цифр – такое число двузначное (14, 28, 67, 93);
• Если натуральное число состоит из трёх цифр – такое число трёхзначное (185, 681, 792, 999);

И так далее числа могут быть четырёх- пяти- шестизначные.

2. Разряды и классы.

• Разряды:

Существует три разряда чисел: сотни, десятки и единицы, слева направо.

• Классы:

Три разряда натурального числа (сотни единицы и десятки вместе) образуют классы (единицы, тысячи, миллионы, миллиарды и так далее).

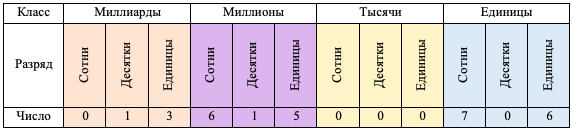
Например, число 13 615 000 706:

При произношении числа читаются все классы кроме единиц. Разряды не читаются. Те классы, где все числа равны 0 – тоже не читаются.

Получим что 13 615 000 706 – это 13 миллиардов 615 миллионов 706

СЛОЖЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ:

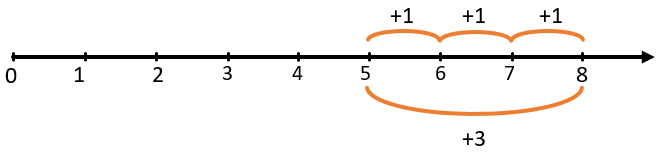
Сложить два натуральных числа – это значит прибавить к одному числу количество единиц второго числа:

$5 + 3 = 5 + 1 + 1 + 1 = 6 + 1 + 1 = 7 + 1 = 8$

Если a + b = c, то a и b – слагаемые, а c – сумма

Например, $5 + 3 = 8:\$

5 – первое слагаемое, 3 – второе слагаемое, 8 – их сумма.

СВОЙСТВА СЛОЖЕНИЯ:

1. Сумма чисел не меняется при перестановке слагаемых (переместительное свойство):

$a + b = b + a$

Например: $4 + 2 = 2 + 4 = 6.$

2. Чтобы прибавить к числу сумму двух других чисел, надо прибавить первое слагаемое этой суммы, а оптом второе (сочетательное свойство):

$a + (b + c) = a + b + c$

Например: $2 + (7 + 1) = 2 + 7 + 1 = 9 + 1 = 10\ или\ (7 + 1) + 2 = 7 + 1 + 2 = 8 + 2 = 10.$

3. От прибавления числа 0 сумма не меняется:

$a + 0 = a$

Например: $6 + 0 = 6.$

ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ:

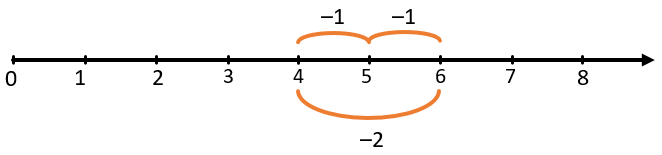
$2 + ? = 6$

$6–2 = 4$

Если $\mathbf{c}\mathbf{–}\mathbf{a}\mathbf{=}\mathbf{b}$, то с – уменьшаемое, a – вычитаемое, а b – разность.

Например$,\ 6–2 = 4:$

6 – уменьшаемое, 3 – вычитаемое, 8 – их разность.

При действиях с натуральными числами вычитаемое не может быть больше уменьшаемого.

Таким образом разность чисел показывает, НА сколько уменьшаемое больше вычитаемого.

СВОЙСТВА ВЫЧИТАНИЯ:

1. Вычитание суммы из числа – чтобы вычесть из числа сумму двух других, можно вычесть сначала первое слагаемое, а потом второе:

$a–(b + c) = a–b–c$

Например: $8\ –(3 + 2) = 8–3–2 = 5–2 = 3.$

2. Вычитание числа из суммы – чтобы вычесть число из суммы, можно вычесть его из одного слагаемого и прибавить к полученной разности второе:

$(a + b)–c = a + b–c = (b–c) + a = (a–c) + b$

Например: $(6 + 3)–2 = 6 + 3–2 = 6 + (3–2) = 6 + 1 = 7.$

3. Если из числа вычесть 0, то разность не изменится:

$a–0 = a$

Например: $7–0 = 7.$

4. Если из числа вычесть его же, то получится 0:

$a–a = 0$

Например: $4–4 = 0.$

УМНОЖЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ:

Например:

$25 \bullet 3\ = \ 25 + 25 + 25 = 75$

Мы нашли сумму трёх слагаемых, каждое из которых равно $25\ (n = 3,\ \ m = 25).$

Если $\mathbf{m \bullet n\ = \ k}$, то m и n – множители, а k – их произведение.

Например: $25 \bullet 3 = 75$, 25 – первый множитель, 3 – второй множитель, 75 – произведение.

СВОЙСТВА УМНОЖЕНИЯ:

1. Произведение не меняется от перестановки множителей:

$a \bullet b = b \bullet a$

Например: $4 \bullet 7 = 7 \bullet 4 = 28$.

2. Чтобы умножить число на произведение двух других чисел, можно умножить число на один множитель, а потом на второй:

$a \bullet (b \bullet c) = a \bullet b \bullet c$

Например: $2 \bullet (5 \bullet 3) = 2 \bullet 5 \bullet 3 = 10 \bullet 3$.

3. Произведение числа и 1 равно этому числу:

$a \bullet 1 = a$

Например: $4 \bullet 1 = 4$.

4. произведение числа на 0 равно 0:

$a \bullet 0 = 0$

Например: $9 \bullet 0 = 0$.

СОКРАЩЕННАЯ ЗАПИСЬ УМНОЖЕНИЯ:

Перед буквенными множителями и скобками не ставят знак умножения, например:

$7 \bullet x = 7x$

$a \bullet b \bullet c = abc$

$(a + 8) \bullet (b\ –4\ ) = (a + b)(b\ –4)$

$2 \bullet (9\ –x) = 2(9\ –\ x)$

ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ:

Например:

$12 \bullet \ ?\ = 36$

$36 : 12 = 3$

Если $\mathbf{k}\mathbf{: n = m}$, то k – делимое, n – делитель, а m – их частное.

Например: $36 : 12 = 3$, 36 – делимое, 12 – делитель, 3 – частное.

Частное показывает ВО сколько раз делимое больше делителя.

В действиях с натуральными числами делимое – самое большое число в уравнении. Оно находится произведением делителя и частного. Например:

$x\ :3 = 4$

$x = 3 \bullet 4 = 12$

Чтобы найти делитель, нужно поделить делимое на частное:

$15 : x = 3$

$x = 15 : 3 = 5$

СВОЙСТВА ДЕЛЕНИЯ:

1. При делении любого числа на 1 получается это же число:

$a : 1 = a$

Например: $6 : 1 = 6$

2. При делении числа на такое же, получается 1:

$a : a = 1$

Например: $5 : 5 = 1$

3. При делении 0 на любое число получится 0:

$0 : a = 0$

Например: $0 : 17 = 0$

4. На ноль делить нельзя!

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ С НАТУРАЛЬНЫМИ ЧИСЛАМИ:

1. Сначала выполняются действия в скобках, если они есть.
2. Дальше выполняется умножение и деление. Если таких действий несколько, они обычно выполняются слева направо (хотя для упрощения счёта порядок можно менять, но только внутри однородных операций, не связанных скобками).
3. После этого выполняется сложение и вычитание. (хотя для упрощения счёта порядок можно менять, но только внутри однородных операций, не связанных скобками).
4. Если в скобках несколько действий, они выполняются в том же порядке, что и в пунктах 1, 2 и 3.

Например:

$19 + 48 : 3\ –\ (28\ –\ 13) \bullet 2 =$

1) Действие в скобках: $28–13 = 15$

2) Слева направо первым идёт деление:

$48\ :3 = 16$

3) После него умножение: $15 \bullet 2 = 30$

4) Теперь сложение и вычитание. Первое слева сложение: $19 + 16 = 35$

5) Последнее – вычитание: $35–30 = 5$

$19 + 48 : 3\ –\ (28\ –\ 13) \bullet 2 = 5$