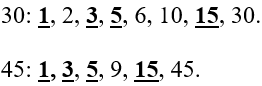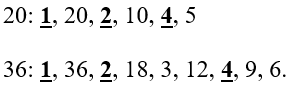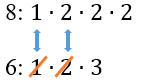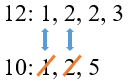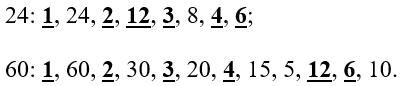НОК и НОД
Рассмотрим выражение:
\(45:9\)
Можем сказать, что 45 – делимое, а 9 – делитель данного выражения.
Мы знаем, что 45 делится нацело на число 9. В таком случае, если мы захотим описать, чем эти числа являются друг другу, то мы скажем, что
9 – делитель числа 45
45 – кратно числу 9
Иногда при решении задач нужно находить общие кратные или общие делители двух чисел.
Наименьший делитель двух чисел – всегда единица. Такой делитель нет смысла искать, поэтому ищут наибольший общий делитель.
НОД:
Рассмотрим числа 30 и 45.
-
Найдем все их существующие делители, т.е. числа, на которые каждое из них поделится нацело:
-
Мы видим, что у этих двух чисел есть несколько общих делителей. Наибольший из них – 15 – является самым большим. Это и есть НОД.
Значит и число 45 и число 30 можно нацело поделить на 15. Записывают это так:
\(НОД\ (30;45) = 15\)
Ответ: 15.
Найдем \(НОД\ (20;36):\)
-
Выпишем все делители этих чисел.
Так же делители можно сразу записывать парой. Если 20 нацело делится на 2, то
\(20\ :\ 2 = 10\)
Значит 10 – тоже делитель числа 20. Запишем делители 2 и 10 парой:
-
Выделим все общие делители и найдем наибольший из них. В данном случае
\(НОД(20;35) = 4.\)
Ответ: 4.
НОК:
Найдем \(НОК\ (10;12).\)
-
Возьмем наименьшее число. В данном случае – 10.
Будем умножать его на натуральные числа по порядку, пока не получим число, кратное 12, то есть такое, на которое нацело поделится и 10, и 12. Оно и будет НОК этих двух чисел. Такой метод называется методом подбора.
\(10 \bullet 1 = 10;\ \ \ \ 10\ НЕ\ кратно\ 12\)
\(10 \bullet 2 = 20;\ \ \ \ 20\ НЕ\ кратно\ 12\)
\(10 \bullet 3 = 30;\ \ \ \ 30\ НЕ\ кратно\ 12\)
\(10 \bullet 4 = 40;\ \ \ \ 40\ НЕ\ кратно\ 12\)
\(10 \bullet 5 = 50;\ \ \ \ 50\ НЕ\ кратно\ 12\)
\(10 \bullet 6 = 60;\ \ \ \ 60\ кратно\ 12\)
-
Первое число, которое будет кратно обоим числам и является их наименьшим общим кратным.
Общих кратный, в отличии от делителей, бесконечно много, поэтому обычно выбирают наименьший их них.
Ответ: 60.
Также можно находить НОК через разложение на множители:
Найдём \(НОК\ (6;8):\)
-
Разложим числа 6 и 8 на простейшие множители, т.е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:
8: \(1 \bullet 2 \bullet 2 \bullet 2\)
6: \(1 \bullet 2 \bullet 3\)
-
Видим, что множители 1 и 2 повторяются у обоих чисел, поэтому для меньшего числа их уберем. Останется:
-
Перемножим все оставшиеся числа. Их произведение и будет НОК:
\(НОК\ (6;\ 8) = 1 \bullet 2 \bullet 2 \bullet 2 \bullet 3 = 24\)
Ответ: 24.
Найдем \(НОК\ (10;12)\) разложением на множители:
-
Разложим оба числа на простые множители. Сверху запишем большее число:
12: 1, 2, 2, 3
10: 1, 2, 5
-
Для меньшего числа зачеркнем те множители, которые уже есть у большего числа:
-
Перемножим все оставшиеся числа:
\(НОК\ (10;\ 12) = 1 \bullet 2 \bullet 2 \bullet 3 \bullet 5 = 60\)
Наш ответ совпал с ответом, где мы использовали метод подбора.
Ответ: 60.
ВЗАИМОСВЯЗЬ НОК И НОД:
Произведение НОК и НОД некоторых чисел равно произведению самих этих чисел:
\(НОК(a;\ b) \bullet НОД(a;\ b) = a \bullet b\)
Докажем эту формулу на примере.
Рассмотрим пару чисел 24 и 60.
-
Найдем их НОД:
\(НОД\ (24;60) = 12\)
-
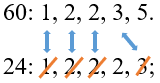
Найдем их НОК:
\(НОК\ (24;\ 60)\ = \ 1 \bullet 2 \bullet 2 \bullet 2 \bullet 3 \bullet 5 = 120\)
-
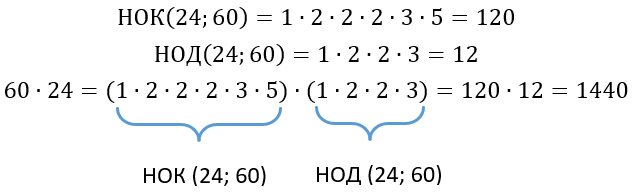
Рассмотрим поближе НОК. Чтобы его получить, мы переменожили все простые множители чисел 60 и 24 за исключением множителей 1, 2, 2, 3. Найдем отдельно их произведение:
\(1 \bullet 2 \bullet 2 \bullet 3 = 12\)
Если перемножить все простые множители числе 60 и 24 мы получим просто их произведение, при этом оно будет состоять из НОК и числа 12, которое в свою очередь равно НОД: