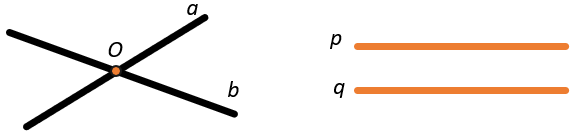Элементы планиметрии
Элементы планиметрии
Точка и прямая — элементы планиметрии, которым трудно дать определение, поэтому их принимают за данность.
Утверждения, которые НЕ требуют доказательств, называются аксиомами.
Утверждения, которые требуют доказательств, называются теоремами.
Аксиома: через любые две точки можно провести прямую, причём только одну.
Обозначения прямой и точки: точка обозначается заглавной латинской буквой (А), прямая – двумя заглавными латинскими буквами (ВС) или маленькой латинской буквой (а).
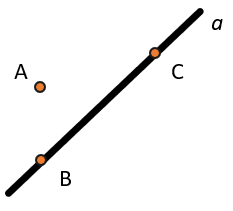
На данном чертеже мы видим несколько точек: А, В и С. Точки В и С образуют прямую a (по аксиоме №1). Тогда мы говорим, что В и С лежат на прямой a или принадлежат ей. В математике это обозначается как \(В \in а,\ С \in а\) или \(В,С \in а.\) Как мы видим, точка А не лежит на прямой а, тогда А не принадлежит или \(А \notin а\).
ПРЯМАЯ:
1. Расположение прямых на плоскости:
- Две прямые могут пересекаться \((а \cap b\)), тогда прямые будут иметь одну общую точку.
- Две прямые могут быть параллельны (\(p\| q\)), тогда прямые не имеют общих точек.
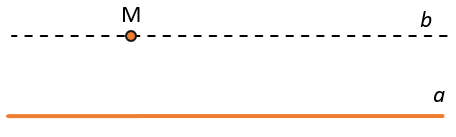
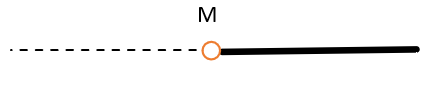
2. Аксиома: через точку, не лежащую на данной прямой (\(М \notin а\)), можно провести на плоскости только одну прямую (\(М \in b)\), параллельную данной (\(a\| b\)):
ОТРЕЗОК:
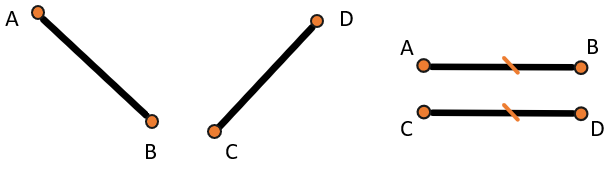
Каждый отрезок имеет свою длину, это значит, что отрезки можно сравнивать. Зная их длину, можно сказать, какой отрезок больше, а какой меньше. Отрезки называются равными, если у них одинаковая длина.
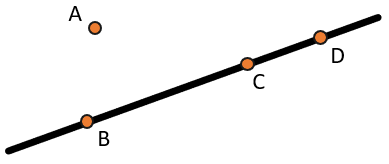
Сравнить длину можно, если мы уже знаем, чему равна длина каждого отрезка (например, измерили линейкой) или путем наложения: если один отрезок наложить на другой, то одинаковые отрезки совпадут. Равные отрезки отмечаются одинаковым количеством черточек (АВ=СD):
ЛУЧ:
Аксиома: на любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
Аксиома: от любого луча в заданную сторону можно отложить угол, равный заданному неразвернутому углу, и притом только один.
Эти аксиомы позволяют сравнивать отрезки и углы в привычном нам формате рассуждений (через наложение отрезков и углов друг на друга).
УГОЛ:
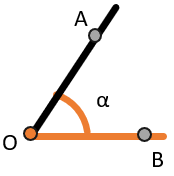
(\(\alpha,\ \beta,\ \gamma\ldots\)), либо по точкам, которые принадлежат лучам (сторонам угла). Например, угол α состоит из двух лучей ОА и ОВ, исходящие из одной вершины – точки О. Значит угол α может назвать углом О (\(\angle\)О) или углом АОВ (\(\angle\)АОВ)
Виды углов:
-
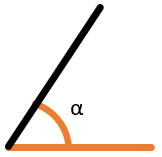
Острый угол ( \(\alpha < 90⁰\) )
-
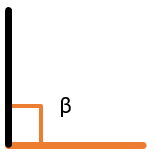
Прямой угол ( \(\beta = 90⁰\) )
-
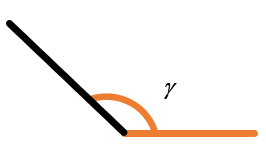
Тупой угол ( \(\gamma > 90{^\circ}\) )
-
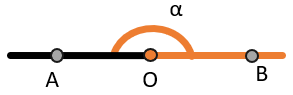
Развернутый угол ( \(\alpha = 180{^\circ}\) )
Если два луча, которые образуют угол, лежат на одной прямой, то тогда такой угол равен 180⁰ и называется развернутым.
Биссектриса угла:
Например:
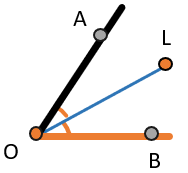
OL – биссектриса угла AOB. Значит \(\angle\)AOL = \(\angle\)LOB. Равные углы обозначаются одинаковым количеством черточек у вершины угла.
Важно помнить, что любая точка биссектрисы равноудалена (находится на равном расстоянии) от сторон угла.

Наши социальные сети
Подписывайся!
Экономь время
на подготовке в ТГ
Забирай полезные чек-листы, памятки и лайфхаки
Подписаться →

Изучай новое
без усилий в ВК
Смотри полезные видео и вебинары, где объясняем сложное простым языком
Подписаться →

Забирай полезное в Максимум БЛОГЕ
Узнай первым лайфхаки по решению заданий предстоящего экзамена
Подписаться →

Содержание