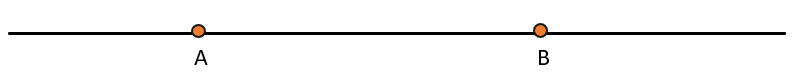Линии

Мы можем рисовать абсолютно любые линии на плоскости. Они могут быть прямыми или зигзагообразными, плавными и круглыми. В математике в основном используют прямые и замкнутые линии.

Если линия не изгибается и не поворачивается, то она называется прямой.

Достаточно двух точек, чтобы провести прямую. Через две точки может проходить только одна прямая:

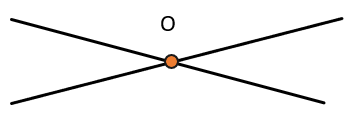
Если две прямые пересекаются, то они имеют одну общую точку:

Если поставить точку и провести от нее в одну сторону линию, то такая линия называется лучом. У луча нет длины, потому что продлевать его можно бесконечно долго. Точка, из которой выходит луч, называется началом луча.

ОТРЕЗОК:

Возьмем две точки А и В. Проведем между ними линию.

Такая линия называется отрезком. Прямую как бы «отрезали» двумя точками. Обозначается он как АВ.

Между двумя точками можно провести только один отрезок. Расстояние между этими точками будет являться длиной отрезка.

Если отрезки АВ и CD имеют одинаковые длины, их равенство записывают как \(\text{AB} = \text{CD}\).

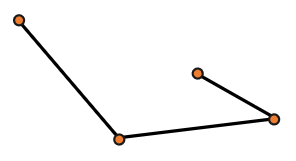
Несколько прямых отрезков могут образовывать непрямую линию, если конец одного отрезка является началом другого. Например:

Такая линия называется незамкнутой.

Чтобы найти длину ломаной линии, нужно найти длины всех отрезков, из которых она состоит, и сложить их.

ФИГУРЫ:

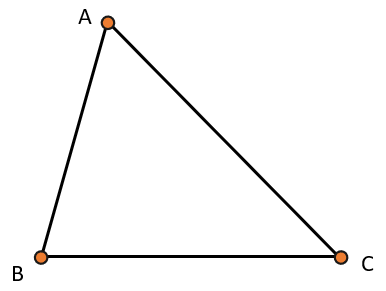
Если концом всей линии является начало первого отрезка, то такая линия – замкнутая. Замкнутые линии образуют фигуры.

Отрезки АВ, ВС и СА – стороны треугольника АВС, а точки А, В и С – его вершины.

Замкнутая линия из четырёх отрезков – четырехугольник, из пяти – пятиугольник и так далее:

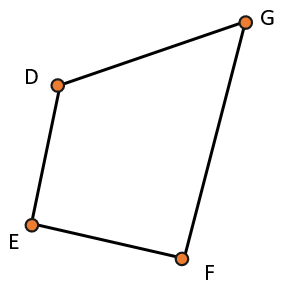
- Стороны четырёхугольника DEFG – отрезки DE, EF, FG, GD. Его вершины – D, E, F, G.

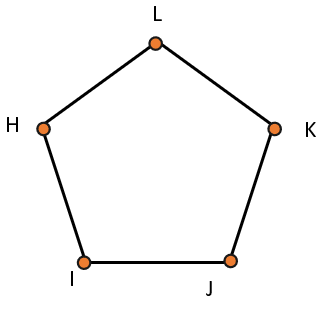
- Стороны пятиугольника HIJKL – отрезки HI, IJ, JK, KL, LH. Его вершины – H, I, J, K, L.

Такие фигуры, как треугольник, четырёхугольник, пятиугольник и т.д. называются многоугольниками.

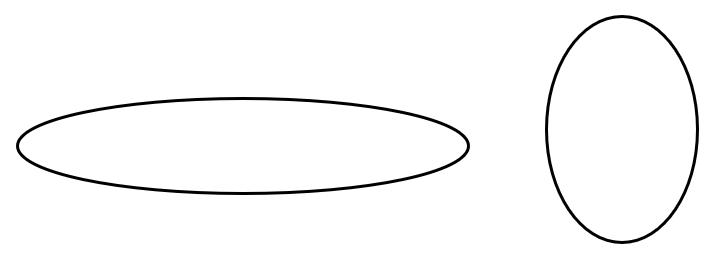
Существуют фигуры, которые являются замкнутыми линиями, но при этом они не образуют углов. Такие фигуры могут быть овалами, эллипсами или окружностями. Нельзя сказать, что они состоят из отрезков:

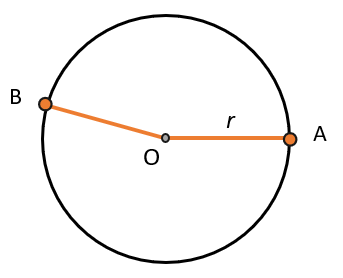
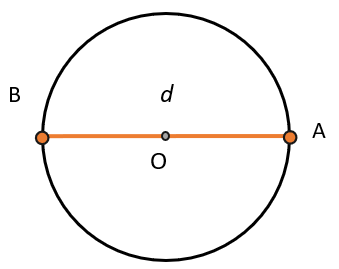
Если все точки на линии находится на одинаковом расстоянии от центра этой фигуры, то такая фигура – окружность. Говорят, что у окружности все точки равноудалены от её центра O на расстояние r – радиус окружности. \(ОА = ОВ = r\):

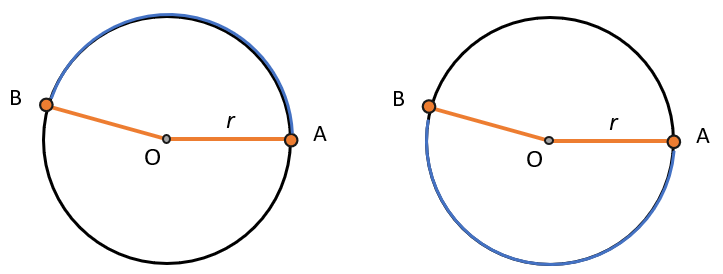
Линии, на которые точки A и В делят окружность, называются дугами.

Если точки А, О и В лежат на одной прямой, то отрезок АВ – диаметр (d).

Диаметр равен: \(d = АО + ОВ\). \(АО = ОВ = r\), значит \(d = r + r = 2r\)