Текстовые задачи на доли и дроби
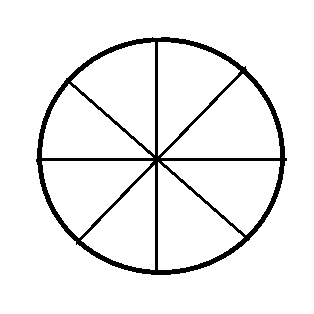
Представим, что мы заказали пирог, разрезанный на одинаковые куски.
Тогда весь пирог может быть обозначен такой дробью:\(\ \frac{8}{8}\)
Число внизу, показывает, на сколько частей поделили целое, и называется «знаменатель». Число сверху, показывает, сколько таких частей возьмут, и называется «числитель». Так как мы пока не брали ни одного кусочка, то числитель и знаменатель обозначены одинаковыми числами.
Если же мы возьмем один кусочек, то мы возьмем 1 из 8 кусочков, то есть \(\frac{1}{8}\)
Числа, у которых в числителе стоит единица, называют: доли.
\(\frac{1}{8}\), \(\frac{1}{3}\), \(\frac{1}{6}\) – это доли.
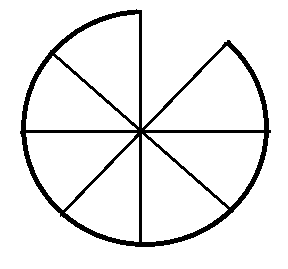
Если же мы возьмем 4 куска пиццы из 8, то дробь будет выглядеть так \(\frac{4}{8}\) .
Дроби используются, когда нужно показать часть относительного некоторого целого. Дроби можно сокращать = делить
расширять = умножать
Например,\(\ \frac{4}{6} = \frac{2}{3}\)
-
От деревянной доски длиной 10 м отрезали 4 м. Какую часть доски отрезали?
Решение:
Итак, нам нужно найти часть, на которую поделили целое.
Отрезали 4 м – то есть отрезали часть (записываем в числитель),
Длина всей доски 10 м – целое (записываем в знаменатель).
\(\frac{длина\ отрезанной\ части}{длина\ всей\ доски} = \frac{4}{10} = 0,4\)
-
В вазе 45 цветов, из них 7 ромашек, остальные тюльпаны. Какую часть составляют тюльпаны от всех цветов?
Решение:
Найдем ту часть, про которую спрашивают в задаче:
45 – 7 = 38 – тюльпаны
38 – часть тюльпанов (записываем в числитель)
45 – целое, т.е. все цветы (записываем в знаменатель)
\(\frac{тюльпаны}{все\ цветы} = \frac{38}{45}\)
Нахождение целого по части и части по его целому
Чтобы найти часть по целому, нужно число, соответствующее целому, умножить на данную в условии дробь.
Чтобы найти целое по части, нужно число, соответствующее части, разделить на данную в условии дробь.
Имеется атласная лента длиной 20 см. Сколько составляет \(\frac{3}{4}\) этой длины?
Решение:
В задаче нужно найти часть
20 см – вся длина, то есть целое. И дана дробь \(\frac{3}{4}\), которая показывает сколько занимает отрезок, длину которого нам нужно найти.
Для того, чтобы найти длину части необходимо целое умножить на данную дробь.
\(20 \cdot \frac{3}{4} = 15\)
15 см составляет \(\frac{3}{4}\) всей длины.
От атласной ленты отрезали 15 см, что составляет \(\frac{3}{4}\) всей длины атласной ленты. Какой длины была лента первоначально?
Решение:
В задаче нужно найти целое.
15 см – это та часть, которую отрезали. Значит, 15 нужно разделить на дробь:
\(15:\frac{3}{4} = 15 \cdot \frac{4}{3} = 20\)
20 см – длина всей ленты.