Конденсатор
Насколько ты знаешь эту тему?
Проверь себя и разбери результаты с экспертом
пройти тест

Конденсатор
Ток — это направленное движение заряженных частиц. Ток в проводниках создается перемещением электронов, так как они могут двигаться в материале свободно, в отличие от зафиксированных в узлах решеток атомов.
Сила тока равна величине заряда, проходящего в единицу времени через проводник \(I = \frac{q}{t}\), где:
\(I\) — сила тока, \(\lbrack A\rbrack\);
\(q\) — перемещенный через проводник заряд, \(\lbrack Кл\rbrack\);
\(t\) — время перемещения заряда, \(\lbrack с\rbrack\);
Проводник, через который проходит заряд, оказывает определенное сопротивление перемещению этого заряда. Связь между разностью потенциалов на концах проводника (напряжением), силой тока в участке цепи, и сопротивлением цепи носит название закона Ома.
Закон Ома для участка цепи имеет вид
\(I = \frac{U}{R}\), где:
\(I\) — сила тока \(\lbrack A\rbrack\);
\(U\) — напряжение (разность потенциалов) \(\lbrack B\rbrack\);
\(R\) — сопротивление \(\lbrack Ом\rbrack\);
Сопротивление проводника — это его физическая характеристика, не зависящая от силы тока в цепи или напряжения, и зависящая только от размеров проводника и материала из которого он изготовлен.
Сопротивление проводника равно \(R = \frac{\text{ρl}}{S}\), где
\(R\) — сопротивление \(\lbrack Ом\rbrack\);
\(I\) — длина проводника \(\lbrack м\rbrack\);
\(\rho\) — удельное сопротивление проводника \(\lbrack Ом\ \cdot м\rbrack\);
\(S\) — площадь поперечного сечения проводника \(\lbrack м^{2}\rbrack\)
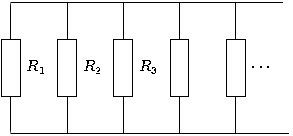
Параллельное и последовательное соединение проводников.
При последовательном соединении общее сопротивление равно сумме сопротивлений всех источников сопротивления \(R = R_{1} + R_{2} + R_{3} + \ldots + R_{n - 1} + R_{n}\), где
R — общее сопротивление всех источников сопротивления, \(\lbrack Ом\rbrack\)
\(R_{1},R_{2},R_{3},\ldots,R_{n - 1},R_{n}\)
сопротивление каждого из источников сопротивления в цепи, \(\lbrack Ом\rbrack\)
\(n\) — количество всех источников сопротивления в цепи.
Сила тока на каждом из источников сопротивления при последовательном соединении, и общая сила тока на участке цепи, одинаковы\(\ I = I_{1} = I_{2} = I_{3} = \ldots = I_{n - 1} = I_{n}\), где
\(I\) — сила тока на участке цепи, \(\lbrack A\rbrack\)
\(I_{1},I_{2},I_{3},\ldots,I_{n - 1},I_{n} -\)сила тока на каждом из источников сопротивления в цепи, \(\lbrack A\rbrack\)
Напряжение в участке цепи равно сумме напряжений на каждом из источников сопротивления
\(U = U_{1} + U_{2} + U_{3} + \ldots + U_{n - 1} + U_{n}\), где
\(U\) — напряжение на участке цепи, \(\lbrack B\rbrack\)
\(U_{1},U_{2},U_{3},\ldots,U_{n - 1},U_{n} -\)напряжение на каждом из источников сопротивления в цепи, \(\lbrack B\rbrack\)
При параллельном соединении общее сопротивление источников сопротивления вычисляется как \(\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} + \ldots + \frac{1}{R_{n - 1}} + \frac{1}{R_{n}}\).
Общее сопротивление двух параллельно соединенных резисторов равно
\(R = \frac{R_{1} \bullet R_{2}}{R_{1} + R_{2}}\).
Сила тока в цепи при параллельном соединении равна \(I = I_{1} + I_{2} + I_{3} + \ldots + I_{n - 1} + I_{n}\).
Напряжение в цепи и на каждом из источников сопротивления одинаковы \(\ U = U_{1} = U_{2} = U_{3} = \ldots = U_{n - 1} = U_{n}\).
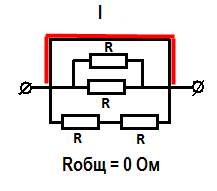
Заряженные частицы в цепи всегда стремятся перемещаться по пути наименьшего сопротивления. Если хотя бы одна из ветвей цепи не нагружена сопротивлением — то весь ток будет перемещаться по ней. На рисунке показан пример цепи, у которой одна из ветвей — верхняя — не имеет сопротивления. Именно по ней пройдет весь ток, а общее сопротивление цепи будет равно нулю.
Конденсатор
Основная характеристика конденсатора — электроемкость или просто емкость С, определяемая как отношение заряда одной из обкладок конденсатора к разности потенциалов, т.е. напряжению между обкладками:
\(C = \frac{q}{U}\),
где \(C\) — емкость конденсатора \(\lbrack Ф\rbrack\);
\(q\) — заряд одной из обкладок конденсатора \(\lbrack Кл\rbrack\);
\(U\) — напряжение между обкладками \(\lbrack B\rbrack\).
При этом в емкость конденсатора не зависит от его заряда и определяется только его геометрическими параметрами (формой, размером и расстоянием между обкладками) и характеристиками материала, которым заполнено пространство между обкладками конденсатора. Напряжение (разность потенциалов) между обкладками будет устанавливаться в зависимости от того заряда, который сообщен конденсатору.
Единицы емкости. В СИ за единицу электроемкости принят фарад (Ф). Емкостью 1 Ф обладает конденсатор, между обкладками которого устанавливается напряжение в 1В при сообщении ему заряда 1 Кл:
\(1\ \left\lbrack Ф \right\rbrack = \frac{1\ \lbrack Кл\rbrack}{1\ \lbrack В\rbrack}\).
На практике обычно приходится иметь дело с конденсаторами, емкость которых значительно меньше 1 Ф, поэтому используются доли этой единицы — микрофарад (мкФ), пикофарад (пФ): 1мкФ = 10-6Ф, 1пФ = 10-6мкФ = 10-12Ф.
Емкость плоского конденсатора.
Простейший конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским.
Его емкость рассчитывается по следующей формуле:
\(C = \frac{\varepsilon\varepsilon_{0}S}{d}\),
где \(C\) — емкость конденсатора \(\left\lbrack Ф \right\rbrack\);
\(\varepsilon ₀\) — электрическая постоянная ,\(( \approx 8,85 \bullet 10^{- 12}\frac{с^{4}А^{2}}{м^{3}\ Кг})\)
\(\varepsilon\) — диэлектрическая проницаемость;
\(S\) — площадь обкладки \(\lbrack м^{2}\rbrack\);
\(d\) — расстояние между обкладками \(\lbrack м\rbrack\).
Пространство между обкладками конденсатора может быть заполнено любым диэлектриком (веществом, не проводящим электрический ток). Диэлектрики характеризуются величиной, называемой диэлектрической проницаемостью.
Диэлектрическая проницаемость \(\varepsilon\) — это безразмерная величина, показывающая во сколько раз напряженность электрического поля (или напряжение между его обкладками) в заполненном диэлектриком конденсаторе меньше, чем в отсутствии диэлектрика при том же заряде конденсатора. Другими словами, диэлектрическая проницаемость показывает, во сколько раз увеличится емкость конденсатора при заполнении его диэлектриком.
У твердых диэлектриков значение ε лежит в пределах от 4 до 7, а для жидких — от 2 до 81.
Батареи конденсаторов
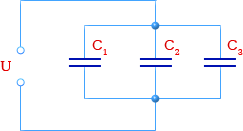
При использовании конденсаторов, их иногда соединяют в батареи. При параллельном соединении n конденсаторов, напряжения U на них одинаковы, а полный заряд q батареи равен сумме зарядов конденсаторов qi, для каждого из которых, очевидно, справедливо \(q_{i} = C_{i}U\).
Рассматривая батарею как один конденсатор, получаем q = CU, другой стороны q = q1 + q2+ … + qn = (C1 + C2 + … + Cn)U.
Получаем, что емкость батареи параллельно соединенных конденсаторов равна сумме емкостей этих конденсаторов: C = C1 + C2 + … + Cn.
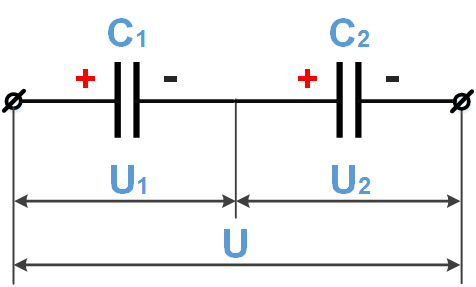
Аналогично рассуждая для последовательного соединения конденсаторов, получаем, что емкость такой батареи конденсаторов можно посчитать по формуле:
\(\frac{1}{C} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}} + \ldots\frac{1}{C_{n}}\)....
При последовательном соединении емкость батареи меньше самой малой из емкостей соединенных конденсаторов.
Поле вне и внутри конденсатора. Электрическое поле плоского конденсатора в основном локализовано между пластинами и вне конденсатора равно нулю. Поле внутри конденсатора можно выразить через напряжение следующим образом:
\(E = \frac{U}{d}\).
Энергия плоского конденсатора. Заряженный конденсатор обладает энергией, которая выражается следующим образом через C, q и U:
\(W = \frac{\text{qU}}{2} = \frac{CU^{2}}{2} = \frac{q^{2}}{2C}\)
Очень важно понимать, какую из формул удобнее применять в каждой конкретной задаче. Например, если в задаче изменяется заряда конденсатора, то следует применять формулу \(W = \frac{CU^{2}}{2}\), если же изменяется заряд, то
\(W = \frac{q^{2}}{2C}\).
Энергетические превращения в конденсаторах
Рассмотрим плоский конденсатор с воздушным зазором, подсоединенный к источнику постоянного напряжения U0. Будем раздвигать пластины конденсатора от расстояния d1 до расстояния d2 в двух случаях: предварительно отсоединив конденсатор от источника питания и не отсоединяя конденсатор от источника питания.
В первом случае, заряд на обкладках конденсатора все время остается неизменным q = CU = const, хотя емкость и напряжение изменяются при движении пластин. Зная напряжение на конденсаторе в начальный момент, находим величину этого заряда \(q = C_{1}U_{0} = \frac{\varepsilon_{0}S}{d_{1}}U_{0}\). Посмотрим, как изменится энергия конденсатора в этом случае. Поскольку заряд конденсатора остается неизменным, применим формулу \(W = \frac{q^{2}}{2C}\)и получим:
\(W_{2} - W_{1} = \frac{q^{2}}{2}(\frac{1}{C_{1}} - \frac{1}{C_{2}})\)
Во втором случае, когда конденсатор подсоединен к источнику питания, сохраняться будет напряжение, и изменение энергии конденсатора можно рассчитывать по следующей формуле:
\(W_{2} - W_{1} = \frac{U_{0}^{2}}{2}(C_{2} - C_{1})\)
Катушка индуктивности
Катушка индуктивности — это катушка, свернутая из изолированного проводника. На электрических схемах катушка индуктивности обозначается как 
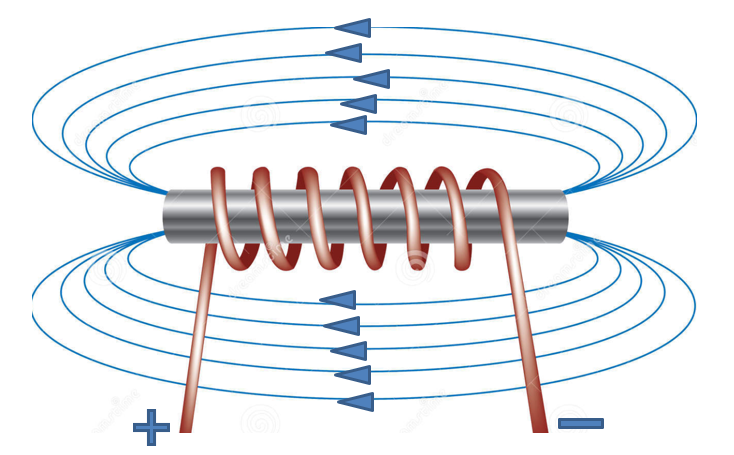
Ток, проходя через проводник, создает магнитное поле. Магнитное поле катушки индуктивности имеет вид:
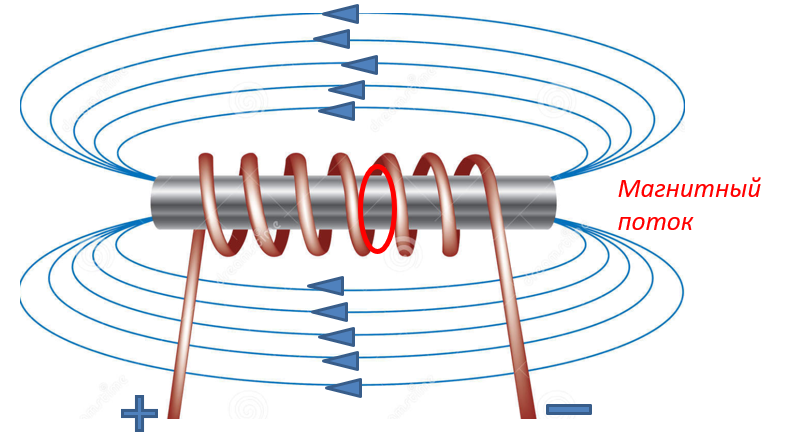
Магнитное поле катушки индуктивности создает магнитный поток. Магнитный поток проходит через катушку и ограничен ее внутренним контуром:
Магнитный поток, который создается ток, протекая через катушку индуктивности, равен\(\ Ф = LI\), где
\(Ф\) — магнитный поток \(\lbrack Вб\rbrack\);
\(L\) — индуктивность \(\lbrack Гн\rbrack\);
\(I\) — сила тока \(\lbrack А\rbrack\).
Магнитный поток, пронизывающий катушку, через которую проходит ток, постоянен. Но если изменяется сила тока в цепи, то, как видно из формулы, изменяется и величина магнитного потока. Согласно правилу Ленца, при изменении магнитного потока, в цепи возникает индукционный ток, который своим магнитным полем стремится возвратить значение магнитного потока. Таким образом, в цепи возникает ЭДС самоиндукции, которая стремится вернуть прежнюю величину тока.

Содержание