Многоугольники

Многоугольники

Многоугольник с наименьшим количеством углов, вершин и сторон является треугольник.

Каждый многоугольник характеризуется площадью и периметром.

ВЫПУКЛЫЙ МНОГОУГОЛЬНИК

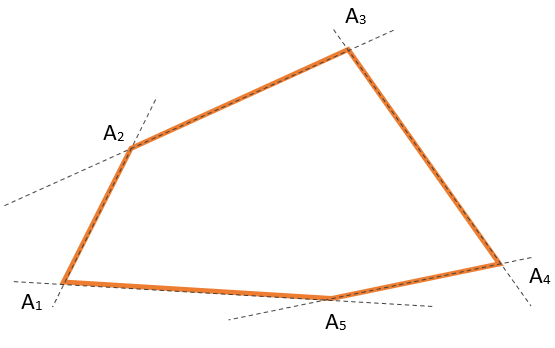
Другими словами, у выпуклого многоугольника любой внутренний угол меньше 180⁰.

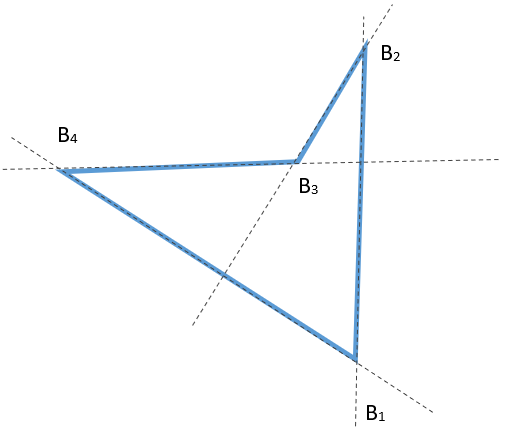
Например, пятиугольник $А_{1}А_{2}А_{3}А_{4}А_{5}$_­ – выпуклый, а четырехугольник $В_{1}В_{2}В_{3}В_{4}$ – невыпуклый или вогнутый:

Далее речь будет идти именно о выпуклых многоугольниках.

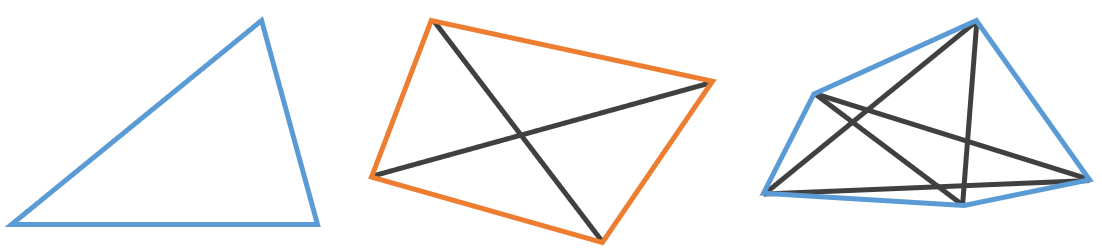
Количество диагоналей в n-угольнике равно

$\frac{n(n\ –\ 3)}{2}$

Таким образом треугольники не имеют диагоналей, т.к. каждая вершина является соседней всем остальным.

ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК

В таком случае каждый угол правильного многоугольника будет равен:

$\frac{(n\ –\ 2) \bullet 180{^\circ}}{n}$

Так же диагонали правильного многоугольника равны.

Периметр правильного n-угольника:

$P = a \bullet n$

где a – длина его стороны.

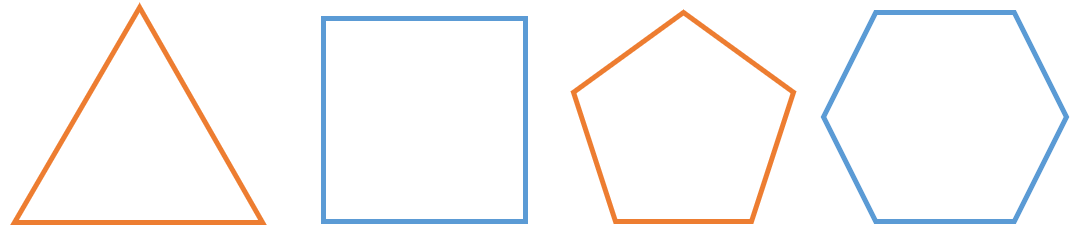
Примерами правильных многоугольников служат правильный треугольник, квадрат, правильный пятиугольник, правильный шестиугольник и т. д.

УГЛЫ, ВЫСОТЫ И ПЛОЩАДИ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ:

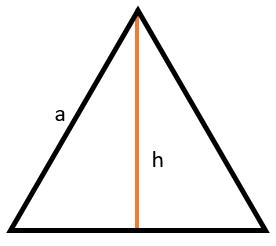
1. Правильный треугольник:

• Все углы правильного треугольника равны по 60⁰
• Высота правильного треугольника равна:

$h = \frac{a\sqrt{3}}{2}$

• Тогда площадь правильного треугольника через его высоту:

$S = \frac{a^{2}\sqrt{3}}{4}$

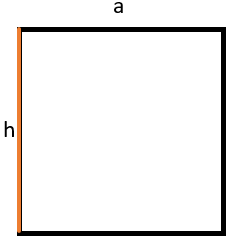
2. Правильный четырёхугольник:

• Все углы квадрата равны по 90⁰
• Высота квадрата (правильного четырёхугольника) равна его стороне:

$h = a$

• Тогда его площадь равна:

$S = a^{2}$

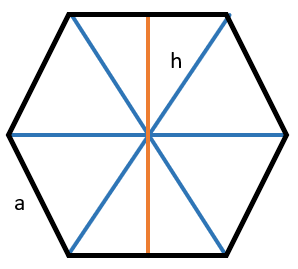
3. Правильный шестиугольник:

• Все углы правильного шестиугольника равны по 120⁰
• Правильный шестиугольник можно представить как шесть одинаковых правильных треугольников. Тогда высота шестиугольника будет равна двум высотам этого треугольника:

$h = a\sqrt{3}$

• Тогда площадь правильного шестиугольника равна площади шести правильных треугольников, из которых он состоит:

$S = \frac{3a^{2}\sqrt{3}}{2}$

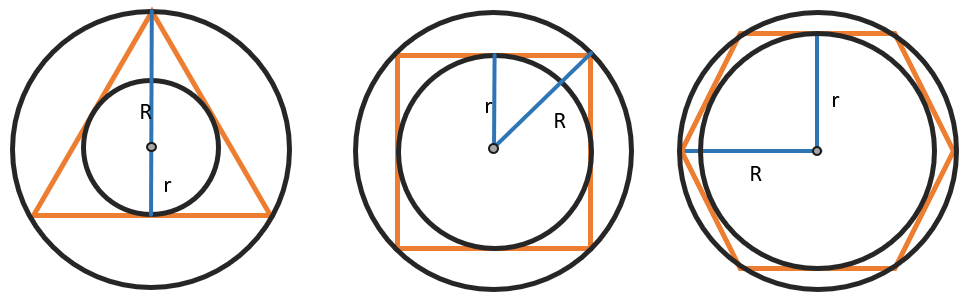
У каждого правильного многоугольника совпадают центры вписанной и описанной окружностей: