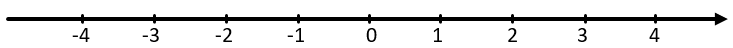Модуль

Модуль

Модуль числа а обозначается как $\left| a \right|$.

Рассмотрим координатную прямую:

1. Найдем модуль числа 3. Чтобы это сделать, нужно посчитать, чему равно расстояние от начала координат до точки с координатой 3 (например А(3)):

$\left| 3 \right| = 3$

2. Найдем модуль числа –3. Так же посчитаем расстояние от начала координат, но уже до точки с координатой –3 (например В(–3)):

Таким образом модуль числа –3 тоже равен трём единичным отрезкам:

$\left| –3 \right| = 3$

Так как модуль – это расстояние, то он не может быть отрицательным, и модули противоположных чисел равны:

$\left| a \right| = \left| –a \right| = a$

3. Если мы попробуем найти модуль числа 0, то увидим, что от точки с координатой 0 до ночала координат нет расстояния, т.к. это одна и та же точка, значит:

$\left| 0 \right| = 0$

Исходя из предыдущих пунктов можно выделить общие правила для модуля:

1. Для положительного числа и нуля модуль равен самому числу.
2. Для отрицательного числа модуль равен противоположному числу.
3. Модули проивоположных чисел равны.

Итак, можно сказать, что $\left| a \right| = a$, если число неотрицательное, и $\left| a \right| = - a$, если число отрицательное. По-другому модуль называется абсолютной величиной числа.