Параллелограммы

Параллелограммы

$AB = CD,\ AD = BC$

$AB\ ||\ CD,\ AD\ ||\ BC$

СВОЙСТВА ПАРАЛЛЕЛОГРАММА:

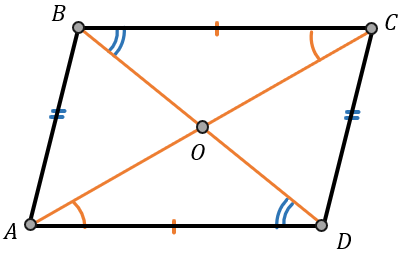
1. Противоположные стороны равны:

$AB = CD$

$AD = BC$

2. Противоположные углы равны:

$\angle A = \angle C$

$\angle B = \angle D$

3. Сумма углов, прилежащих к одной стороне, равна 180°. Это вытекает из параллельности противоположных сторон, так как указанные углы являются односторонними:

$\angle BAD + \angle ADC = 180{^\circ}$

$\angle ABC + \angle BCD = 180{^\circ}$

4. Из параллельности сторон вытекает равенство частей углов. Например:

$\angle DAC = \angle BCA$

$\angle CBD = \angle BDA$

5. Две диагонали делят параллелограмм на две пары равных (по стороне и двум углам) треугольников:

$\mathrm{\Delta}ABC = \mathrm{\Delta}BCD$

$\mathrm{\Delta}ABD = \mathrm{\Delta}ACD$

6. Диагонали параллелограмма точкой пересечения делятся пополам:

$AO = OC$

$BO = OD$

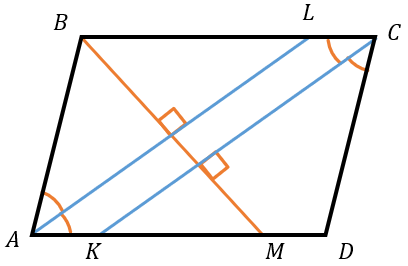
Также параллелограмм обладает необычными свойствами, связанные с биссектрисами:

Пусть AL и СК – биссектрисы противоположных углов, а ВМ – биссектриса смежного с ними угла.

Тогда:

1. Биссектрисы противоположных углов параллельны:

$AL\ ||\ CK$

2. Биссектрисы смежных углов перпендикулярны:

$AL,\ CK\bot BM$

3. Биссектриса параллелограмма отсекает от него два равных угла. Например:

$\mathrm{\Delta}ABL\ - \ равнобедренный,\ т.к.\ \angle BAL = \angle BLA$

$\mathrm{\Delta}ABM\ - \ равнобедренный,\ т.к.\ \angle ABM = \angle AMB$

ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА:

Для того, чтобы доказать, что фигура действительно является параллелограммом, нужно знать, какими свойствами мы можем пользоваться. Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Четырехугольник имеет две пары параллельных сторон:

$AB\ ||\ CD$

$BC\ ||\ AD$

2. Четырехугольник имеет пару параллельных и равных сторон:

$AB\ ||\ CD,\ AB = CD$

$или$

$BC\ ||\ AD,\ BC = AD$

3. В четырехугольнике противоположные стороны попарно равны:

$AB = CD$

$BC = AD$

4. В четырехугольнике противоположные углы попарно равны:

$\angle DAB = \angle BCD$

$\angle ABC = \angle CDA$

5. В четырехугольнике диагонали точкой пересечения делятся пополам:

$AO = OC$

$BO = OD$

6. Сумма углов четырехугольника, прилегающих к любой стороне, равна 180°:

$\angle ABC + \angle BCD = \angle BCD + \angle CDA = \angle CDA + \angle DAB = \angle DAB + \angle ABC = 180{^\circ}$

ПЛОЩАДЬ ПАРАЛЕЛОГРАММА:

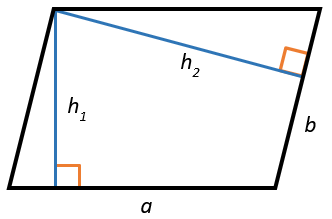
1. Через высоту и сторону

Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

$S = ah_{1} = bh_{2}$

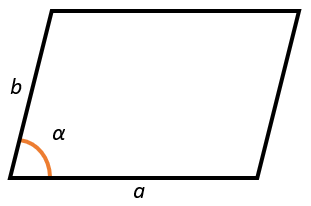
2. Через две стороны и угол между ними

Площадь параллелограмма равна произведению его сторон на синус угла между ними.

$S = ab \bullet \sin\alpha$

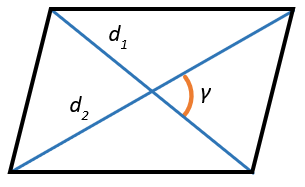
3. Через диагонали и угол между ними

Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

$S = \frac{1}{2}d_{1}d_{2} \bullet \sin\gamma$