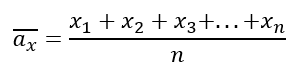Вероятность, комбинаторика и статистика
Основы математической статистики
Работа с основными статистическими терминами обычно осуществляется с какими-либо данными. Например, в классе взвешивали учеников. Вес каждого из них – это данные взвешивания. Для удобства такие данные выписывают в ряд, перечисляя все полученные результаты. Он будет называться числовым рядом.
Именно числовой ряд и анализируют, используя статистические термины и методы.
РАЗМАХ И ЧАСТОТА:
Такая характеристика как размах показывает, на сколько отличаются друг от друга элементы ряда.
Представим числовой ряд, состоящий из натуральных чисел:
3, 11, 18, 18, 22, 37, 37, 37, 89
В данном случае наибольшим числом является 89, а наименьшим 3.
3, 11, 18, 18, 22, 37, 37, 37, 89
Тогда размах данного ряда равен \(89–3 = 86\).
Например, частота числа 3 – 1 раз. А вот число 18 встречается 2 раза.
МОДА И МЕДИАНА:
Чтобы понять, какие средние и популярные значения присутствуют в ряду, используют такие характеристики числового ряда как мода и медиана.
В данном случае это число 37. Оно встречается три раза. Чаще него ни одно другое число не встречается. Значит оно и есть мода.
3, 11, 18, 18, 22, 37, 37, 37, 89
Например, в нашем ряде это число 22.
3, 11, 18, 18, 22, 37, 37, 37, 89
Оно является медианой, потому что в этому ряду существует четыре числа меньше числа 22 и четыре числа больше 22.
Поэтому важно выстраивать элементы по порядку, чтобы сразу заметить медиану.
Если мы добавим еще одно число в наш ряд, например допишем число 15, получим 10 чисел в ряду. Тогда по середине ряда будут находиться уже два числа: 22 и 18:
3, 11, 15, 18, 18, 22, 37, 37, 37, 89
В таком случае, если в ряду находится нечетное количество элементов, его медианой будет среднее арифметическое этих элементов.
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ:
Оно находится по следующей формуле:
Эта запись означает, что чтобы найти среднее арифметическое ряда чисел, нужно сложить все его элементы и разделить на их количество.
Найдем среднее арифметическое пятого и шестого элемента нашего ряда. Оно будет являться медианой, т.к. оба эти элементы стоят в середине ряда:
3, 11, 15, 18, 18, 22, 37, 37, 37, 89
\(m = \frac{18 + 22}{2} = \frac{40}{2} = 20\)
Действительно, если заменить сумму этих элементов на сумму такого же количества средних арифметических, то эта сумма не изменится.
\(18 + 22 = 20 + 20\)
Найдем среднее арифметическое всего ряда. Для этого сложим все элементы и поделим уже на их количество:
\(\overline{a_{x}} = \frac{3 + 11 + 15 + 18 + 18 + 22 + 37 + 37 + 37 + 89}{10} = \frac{287}{10} = 28,7\)
СРЕДНЕЕ ГЕОМЕТРИЧЕСКОЕ:
Оно находится по формуле:
\(\overline{g_{x}} = \sqrt[n]{x_{1}x_{2}x_{3} \bullet ... \bullet x_{n}}\)
Это значит, что чтобы найти среднее геометрическое, нужно перемножить все элементы ряда и извлечь произведение из корня, степень которого равна их количеству.
Возьмем ряд с меньшими количеством элементов:
1, 3, 3, 5, 8
Найдем его среднее геометрическое:
\(\overline{g_{x}} = \sqrt[5]{1 \bullet 3 \bullet 3 \bullet 5 \bullet 8} = \sqrt[5]{360} \approx 3,25\)
В конце года ученику важно получить хорошую оценку за четверть. У него имеются следующие оценки по математике:
4, 3, 5, 5, 4, 4, 2, 4, 5, 5, 3, 4
Полностью проанализируем его оценки, используя статистические характеристики.
1. Для начала сделаем ряд ранжированным, т.е. расставим все его элементы по порядку:
2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5
2. Определим размах ряда. Ученик получал все возможные оценки за четверть и как мы видим, наибольшей является оценка 5, а наименьшей – 2. Тогда размах равен 5 – 2 = 3.
3. Определим моду ряда. Самой часто встречающейся оценкой является оценка 4. Её частота – 5.
4. При этом частота оценки 5 ненамного меньше и равна четырем.
5. Медианой данного ряда будет являться число по середине. Всего у нас 12 элементов ряда, тогда средними значениями будут являть шестой и седьмой элементы.
2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5
Для определения медианы из двух средних значений найдем их среднее арифметическое:
\(m = \frac{4 + 4}{2} = 4\)
Из-за того, что элементы равны между собой, их среднее арифметическое будет таким же. Медиана этого ряда – 4
6. Среднее арифметическое ряда:
\(\overline{a_{x}} = \frac{2 + 3 + 3 + 4 + 4 + 4 + 4 + 4 + 5 + 5 + 5 + 5}{12} = \frac{48}{12} = 4\)
7. Среднее геометрическое ряда:
\(\overline{g_{x}} = \sqrt[12]{2 \bullet 3 \bullet 3 \bullet 4 \bullet 4 \bullet 4 \bullet 4 \bullet 4 \bullet 5 \bullet 5 \bullet 5 \bullet 5} = \sqrt[12]{11520000} \approx 3,88\)
Таким образом мы определили, что за четверть ученик получит среднее арифметическое всех оценок, то есть 4.
Чаще всего ученик получал оценку 4, и она же является медианой. При этом ученик получал за четверть всевозможные оценки, от двоек до пятерок. Среднее геометрическое всех оценок тоже близко к 4.
По-разному проанализировав успеваемость ученика, можно убедиться в точном результате его работы. Ученику можно смело ставить четверку.
Диаграммы, графики и таблицы
Например, рассмотрим такую ситуацию. Ученик неделю наблюдал за погодой. Всего он зафиксировал три вида погоды – облачно, ясно и дождь. Он выяснил следующее:
- в понедельник был дождь
- во вторник было облачно
- в среду было ясно
- в четверг было ясно
- в пятницу было облачно
- в субботу было ясно
- в воскресенье был дождь
Таким списком неудобно представлять информацию. Есть более наглядные методы её визуализации. Рассмотрим их.
ДИАГРАМЫ:
Диаграмма используется, когда нам нужно показать, например, количество дождливых, ясных и облачных дней по сравнению друг с другом.
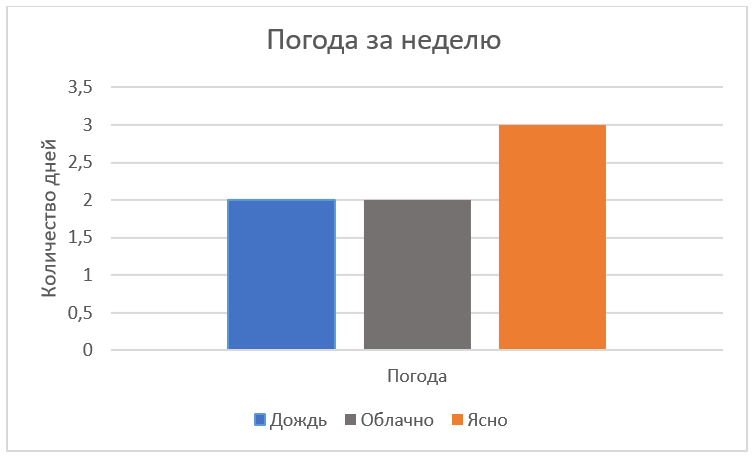
1. Столбчатая диаграмма:
Тогда диаграмма нашего ученика будет выглядеть следующим образом:
Глядя на диаграмму, мы сразу можем проанализировать данные, собранные учеником.
1. По вертикальной оси отмечено количество дней, а на горизонтальной оси подписана зафиксированная погода. Сравнивая количество дней с высотой столбца, мы можем говорить о том, сколько было дней с конкретной погодой и было ли их больше или меньше, чем дней, когда погода на улице была другой.
2. Мы видим, что больше всего было ясных дней, и что дождливых и облачных дней между собой было поровну. Так же мы можем точно сказать, что за неделю ясных дней было 3, а дождливых и облачных – 2.
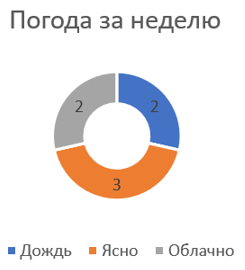
2. Круговая диаграмма:
Диаграммы могут иметь и другой вид, но отображать те же данные. Например, существуют круговые и кольцевые диаграммы.
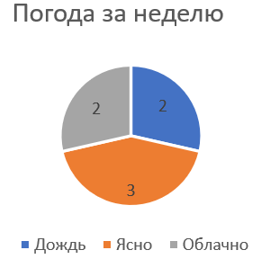
По ним также видно количество дней с разной погодой относительно друг друга. Чем больше заполнена окружность или кольцо определенным типом погоды, тем больше дней по сравнению с другими погодами она наблюдалась.
Обычно данные диаграммы измеряются в процентах. В сумме все цвета на диаграмме равны 100%, а площадь круга или кольца, которую занимает каждый цвет, рассчитывается исходя их процента, который ей соответствует.
Если мы хотим обозначит, например, 50% в диаграмме, то цвет, соответствующий этому событию, займет половину диаграммы. 10% - одну десятую и так далее.
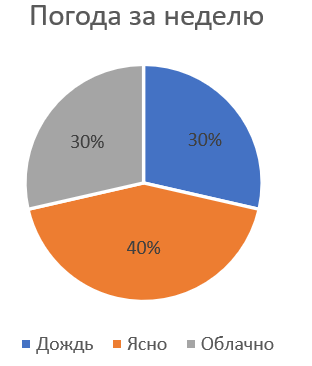
Если мы заменим фактическое количество дней с конкретной погодой на проценты, получим такую диаграмму:
Такие проценты мы получили, поделив количество дней с данной погодой на количество всех дней. Облачная погода и дождь наблюдались в двух из семи днях:
\(\frac{2}{7} \approx 30\%\)
А ясная погода в трёх из семи днях:
\(\frac{3}{7} \approx 40\%\)
В соответствии с цветами для каждой погоды серый и синий цвет займут по 30% площади круга, а оранжевый цвет займет 40%.
В сумме все цвета диаграммы дают 100%.
Теперь по диаграмме мы можем сказать, что 30% дней наблюдалась облачная погода, 30% - дождь и 40% - ясная погода.
ТАБЛИЦЫ:
Возьмем ту же информацию о погоде за неделю. Например, нам нужно не сравнивать количество ясных и облачных дней, а сопоставлять нечисловые данные. В таком случае будет удобнее использовать таблицу:
Нашему ученику нужно указать, в какой день какая погода наблюдалась. В таком случае мы не сможем сделать диаграмму, потому что ни один из дней недели не может быть выше остальных. Составим таблицу, в строчках которых будут обозначены дни недели, а в столбцах – погода:
| Ясно | Облачно | Дождь | |
|---|---|---|---|
| Понедельник | |||
| Вторник | |||
| Среда | |||
| Четверг | |||
| Пятница | |||
| Суббота | |||
| Воскресенье |
На пересечении конкретных строк и столбцов указываются общие данные. Будем постепенно заполнять таблицу. Если в конкретный день недели наблюдалась указанная погода, отметим в ячейке «да», если нет, отметим «нет».
Первая ячейка – понедельник-ясно. Это неверно, такой погоды не было в понедельник. Аналогично с понедельник-облачно. А вот дождь в понедельник действительно был. Отметим это в таблице:
| Ясно | Облачно | Дождь | |
|---|---|---|---|
| Понедельник | нет | нет | да |
| Вторник | |||
| Среда | |||
| Четверг | |||
| Пятница | |||
| Суббота | |||
| Воскресенье |
Аналогично проанализируем остальные дни недели и отметим их:
| Ясно | Облачно | Дождь | |
|---|---|---|---|
| Понедельник | нет | нет | да |
| Вторник | нет | да | нет |
| Среда | да | нет | нет |
| Четверг | да | нет | нет |
| Пятница | нет | да | нет |
| Суббота | да | нет | нет |
| Воскресенье | нет | нет | да |
Такая таблица имеет довольно простой принцип заполнения. Можно, например, вместо «да» и «нет» ставить галочки и крестики. Но чаще всего таблицы служат для большего объёма информации.
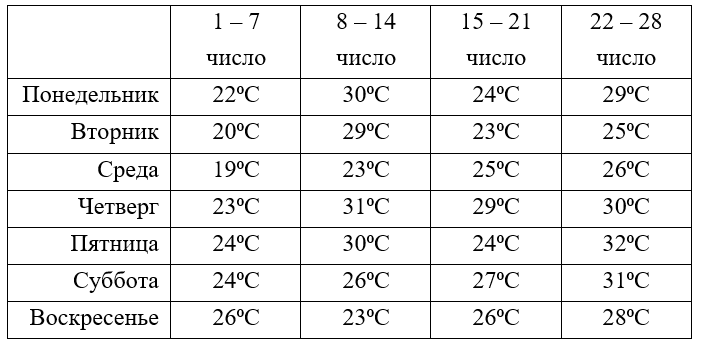
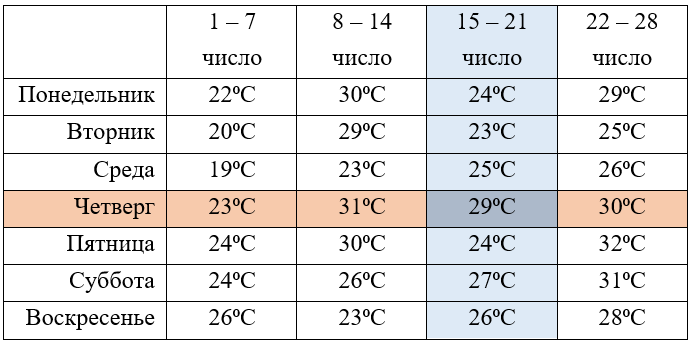
Рассмотрим пример: Представим, что этот же ученик заполнял не просто погоду, а конкретную температуру 4 недели. А весь результат он занес в следующую таблицу:
Видим, что в интересующий нас день температура равнялась 29⁰С. Таким образом мы очень ёмко и понятно записали данные о погоде почти за целый месяц!
ГРАФИКИ:
Еще одним способом визуализации является график.
Пересечение этих характеристик похоже на пересечение столбцов и строк таблицы, но график имеет совершенно другой вид, при этом таблице и аналогичном графике может отображаться та же самая информация. Составим по этой таблице график.
1. Отметим на вертикальной оси графика температуру по возрастанию.
3. В соответствии с температурой конкретного дня поставим на графики току, и все точки для различных дней соединим.
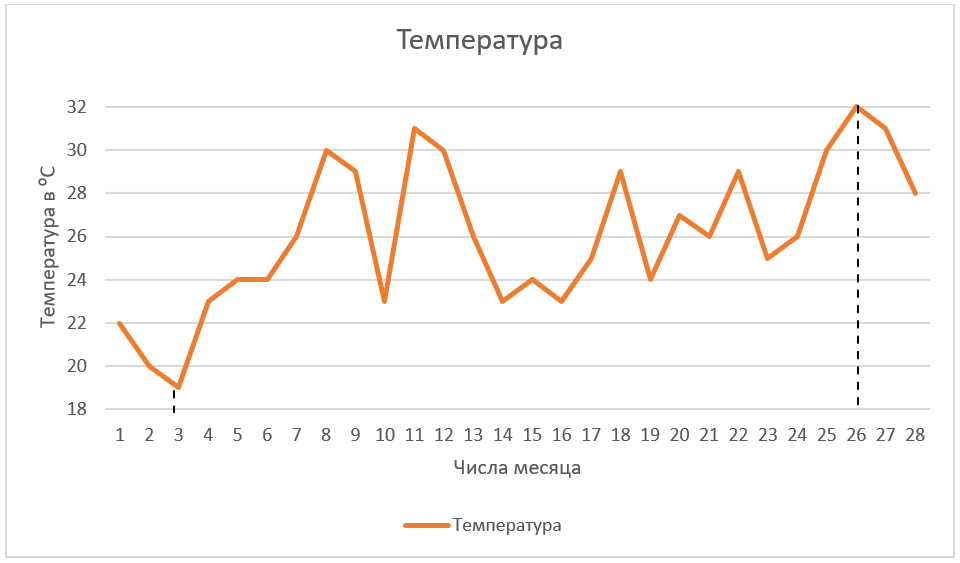
Получим линию, описывающую поведение температуры за заданный промежуток времени:
Таким образом мы можем анализировать, когда была самая высокая, а когда самая низкая температура, можем смотреть, когда температура возрастала, а когда убывала.
Например, самой высокой температура была 26 числа и равнялась она 32⁰С. А самая низкая температура наблюдалась 3 числа и равнялась 19⁰С.
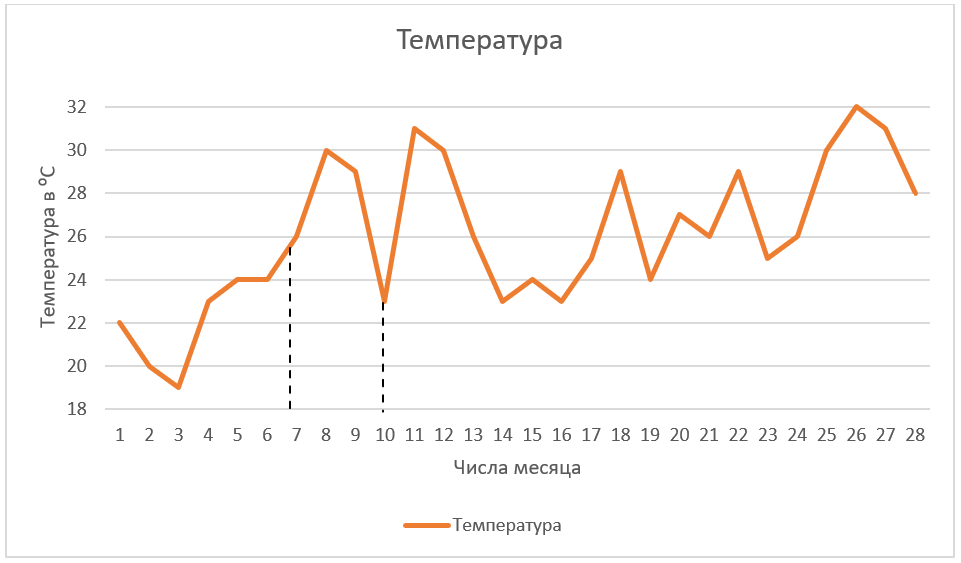
А вот в промежутке с 7 по 10 число, самая высокая температура была 8-ого числа и равнялась 30⁰С.
График позволяет нам не просто сравнивать температуру на всем промежутке времени, но анализировать выбранное нами время отдельно.
Вероятность
\(Вероятность = \frac{количество\ благоприятных\ событий}{количество\ возможных\ событий}\)
Давайте посчитаем вероятность выпадения орла при броске монеты. Назовем событие выпадения орла событием А. Тогда вероятность события А – это Р(А).
Как мы и сказали, благоприятным действием является выпадение орла. Такой исход всего один.
\(Р(А) = \frac{1}{2}\)
Вероятность может выражаться как правильной дробью, так и процентами.
\(Р(А) = \frac{1}{2} \bullet 100\% = 50\%\)
Можем сказать, что вероятность выпадения орла равна 50%, или 0,5.
Ответ: 0,5.
Теперь посчитаем вероятность выпадения решки. Пусть событие выпадения решки – это событие В. Тогда вероятность этого события – это Р(В).
Существует одно благоприятное событие и два возможных, тогда
\(Р(В) = \frac{1}{2} = 0,5\)
Ответ: 0,5.
Получается, что при броске монетки вероятность выпадения орла равна вероятности выпадения решки. Так получается, потому
Сумма всех вероятностей всевозможных событий равна 1 (или 100%).
\(Р(А) + Р(В) = \frac{1}{2} + \frac{1}{2} = 1\)
Если мы будем подкидывать очень много раз монетку и записывать, сколько раз выпал орел, то для более наглядного описания того, как часто орел выпадает, будет использоваться такое понятие как частота.
В урне 12 шаров. 3 из них – белые, 9 – черные.
а) Какова вероятность Р(А) того, что наугад из урны достанут белый шар?
в) Какова вероятность Р(С), что наугад из урны достанут серый шар?
а) Всего можно достать 3 белых шара, то есть у нас есть 3 благоприятных события. А всевозможных событий у нас 12 – это количество всех шаров, тогда:
\(Р(А) = \frac{3}{12} = \frac{1}{4}\)
б) Аналогично можем посчитать вероятность Р(В). Но мы знаем, что в сумме вероятности Р(А) и Р(В) равны единице. Тогда мы можем из единицы вычесть неблагоприятные события, чтобы получить благоприятные:
\(Р(В) = 1\ –\ Р(А) = 1\ –\ \frac{1}{4} = \frac{3}{4}\)
в) Если в урне нет серых шаров, тогда количество благоприятных событий равна 0. В таком случае:
\(Р(С) = \frac{0}{12} = 0\)
Ответ: 0,25; 0,75; 0.
Иногда, когда у нас есть комбинации результатов, приходится считать количество всевозможных комбинаций. Нахождение благоприятных и возможных событий усложняется.
Найдите вероятность того, что при броске двух игральных костей выпадет сумма чисел:
б) не кратная трем.
-
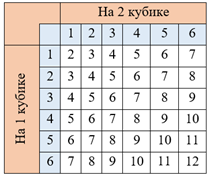
Для начала нам нужно понять, какие вообще комбинации могут выпасть. У нас есть два кубика. На каждом может выпасть число от 1 до 6. На каждое число, выпавшее на одном кубике, может выпасть одно из шести чисел на втором. Представим возможные события в таблице.
Сразу видно, что всевозможных бросков у нас
\(6 \bullet 6 = 36\).
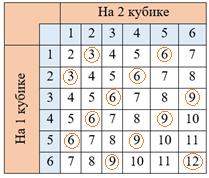
2. Найдем благоприятные события. Пусть сумма выпавших очков на костях кратна 3 – это событие А. Будем записывать в пересечение строк и столбцов сумму соответствующих очков:
-
Из всевозможных сумм выделим те, которые кратны числу 3.
Таких событий всего 12.
4. Теперь можем посчитать вероятность Р(А) по формуле вероятности:
\(Р(А) = \frac{12}{36} = \frac{1}{3}\)
б) Чтобы найти все остальные события, также используем сумму всех вероятностей. Пусть выпадение суммы на костях не кратное трем, это событие В, тогда:
\(Р(В) = 1\ –\ Р(А) = 1\ –\ \frac{1}{3} = \frac{2}{3}\)
Ответ: \(\frac{1}{3}\); \(\frac{2}{3}\).
ВЕРОЯТНОСТЬ НЕСКОЛЬКИХ СОБЫТИЙ:
Когда у нас есть вероятность нескольких событий и нам нужно посчитать, какая у них будет общая вероятность, мы используем сложение и умножение вероятностей.
1. Сложение вероятностей:
\(\mathbf{P(A) + P(B)}\)
Если возможно, что произойдет одно ИЛИ другое событие, тогда вероятности этих событий складываются. В примере №3 мы могли вытащить ИЛИ черный шар ИЛИ белый. Вытащить два шара сразу у нас не получится. Такие события называются взаимоисключающие.
Вероятность того, что в магазине будет продана пара мужской обуви 44-ого размера, равна 0,12, 45-ого – 0,04, 46-ого и больше – 0,01. Какова вероятность, что будет продана пара мужской обуви не меньше 44-ого размера.
1. Может быть куплена только одна из пар обуви не меньше 44-ого размера. То есть 44-ый размер ИЛИ 45 ИЛИ 46 и больше. Тогда вероятности будут складываться:
\(Р(А) = 0,12 + 0,04 + 0,01 = 0,17\)
Ответ: 0,17.
2. Произведение вероятностей:
Если возможно, что произойдет одно И другое событие вместе, тогда вероятности этих событий умножаются. Если бы мы вытягивали шары из одной корзины И из другой одновременно, тогда вероятности вынимания конкретных цветов перемножаются. Такие события называются независимыми, они происходят независимо друг от друга.
\(P\left( A \right) \cdot P(B) = P(AB)\)
Вероятности попадания в цель при стрельбе первого и второго орудия соответственно равны Р(А) = 0,7; Р(В) = 0,6. Какова вероятность, что стрелок сделает по одному выстрелу из каждого орудия и два раза попадет в цель?
1. Стрелок будет стрелять И из первого орудия И из второго. Тогда вероятности будут перемножаться:
\(Р(С) = Р(А) \bullet Р(В) = 0,7 \bullet 0,6 = 0,42\)
Ответ: 0,42.
ТЕОРЕМЫ, ОБЪЕДИНЯЮЩИЕ ВЕРОЯТНОСТИ НЕСКОЛЬКИХ СОБЫТИЙ:
Стоит отметить разницу между суммами вероятностей взаимоисключающих и независимых событий:
Сумма взаимоисключающих событий:
\(P(A) + P(B)\)
Сумма независимых событий:
\(P(A + B)\)
Теорема №1:
Сумма вероятностей двух событий равна сумме вероятности произведения этих событий и вероятности суммы этих событий.
\(P(A) + P(B) = P(A \cdot B) + P(A + B)\)
Теорема №2:
Вероятность суммы двух независимых событий равна разности суммы вероятностей этих событий и произведения вероятностей этих событий.
\(P\left( A + B \right) = P\left( A \right) + P\left( B \right)\ –\ P\left( A \right) \cdot P(B)\)
Два стрелка независимо друг от друга по одному разу стреляют в мишень. Вероятность попадания в мишень каждого стрелка по отдельности равна 0,8 и 0,3 соответственно. Найдите вероятность того, что мишень:
а) будет поражена хотя бы один раз;
1. Пусть попадание в мишень первого стрелка – это событие А. Попадание в мишень второго стрелка – событие В. Тогда \(Р(А) = 0,8,\ \ Р(В) = 0,3.\ А\) и В – независимые события.
а) Мишень будет поражена хотя бы один раз, если в цель попадет первый ИЛИ второй стрелок. Значит будем искать сумму вероятностей событий. Т.к. это события независимые, будем искать \(Р(А\ + \ В)\) по т. №2:
\(P(A + B) = P(A) + P(B)\ –\ P(A)P(B) = 0,8 + 0,3\ –\ 0,24 = 1,1\ –\ 0,24 = 0,86\)
б) Мишень будет поражена ровно один раз, если один стрелок попадет в цель, а второй нет. Можем представить это как такую ситуацию:
В мишень попал первый ИЛИ второй стрелок (\(Р(А + В)\) как в пункте а). Но т.к. эта вероятность включает в себя событие, когда в мишень попадают оба стрелка сразу, её нужно исключить, потому что нам нужно ровно одно попадание из двух. Если А и В – независимые события, тогда вероятность, что произойдут оба из этих событий равна \(Р(АВ)\). Получаем:
\(P(A + B)\ –\ P(AB) = 0,86\ –\ 0,24 = 0,62\)
Ответ: 0,86; 0,62.
Основы комбинаторики
От количества задействованных элементов множества и способов их комбинирования зависит подход к решению задачи. Каждый из типов задач имеет свои специальные формулы для расчета комбинаций, но пока для понимания сути расположения элементов множества проще всего использовать различные визуализации.
ЗАДАЧИ ПЕРВОГО ТИПА:
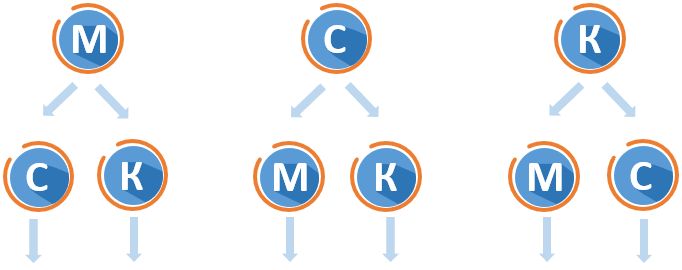
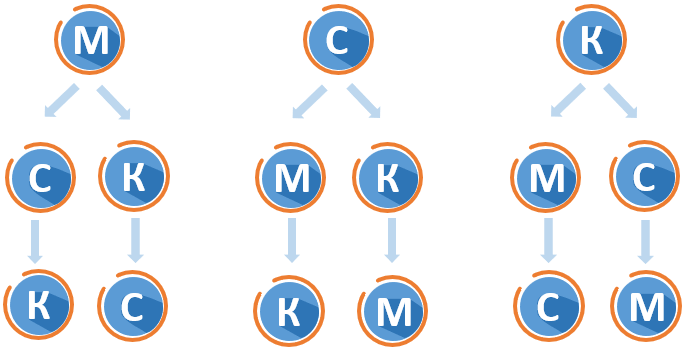
Турист собирается посетить за лето три города – Москву, Санкт-Петербург и Казань. Сколько существует вариантов поездок, если каждый город турист посетит один раз?
1. У нас есть множество, состоящее из трёх городов. Обозначим их как М, С и К. Задачи такого типа отличаются тем, что мы должны комбинировать все элементы множества между собой без повторений.
2. Подумаем, какие варианты поездок существуют. Обозначим три ситуации, где первым город является один из городов:
3. Если города не могут повторяться, тогда после М возможно поехать только в С или К, после С только в М или К, а после К только в М или С. Дополним схему:
4. Если турист уже посетил города в порядке \(M \Rightarrow C\), то ему остается посетить только К. Если он проехал путь \(M \Rightarrow K,\) ему остается посетить только С. Аналогично проанализируем каждый маршрут и заполним схему до конца:
5. В итоге у нас получились следующие комбинации посещения городов: МСК, МКС, СМК, СКМ, КМС, КСМ. Итого 6 различных маршрутов.
Ответ: 6.
ЗАДАЧИ ВТОРОГО ТИПА:
При встрече 7 приятелей пожали друг другу руки. При этом каждый пожал руку с каждым. Сколько всего было рукопожатий?
1. Обычно друг другу жмут руки именно два человека, поэтому будет рассматривать всевозможные пары друзей. Этот тип задач отличается от первого тем, что в наших комбинациях будут участвовать не все 7 элементов множества друзей сразу, а только по два из них. То есть обозначим каждого друга цифрой от 1 до 7 и будем комбинировать из этих чисел пары, они будут являться подмножеством множества друзей.
2. При этом пары, содержащие одинаковые элементы, неважно в каком порядке, считаются одинаковыми. Это значит, что рукопожатия друзей, например, 2 и 7 равно рукопожатию друзей 7 и 2. Будем брать именно ту пару, которая начинается на меньшую цифру. В данном случае рукопожатие именно этих людей запишем как 27.
3. Аналогично примеру №1 будем анализировать друзей по одному. Выпишем, какому количеству человек может пожать руку первый приятель:
12, 13, 14, 15, 16, 17 – 6 раз пожмёт кому-либо руку первый друг.
Сам себе он пожать руку не может, поэтому получилось 7 – 1 = 6 рукопожатий
4. Второй друг пожмёт руку друзьям такими комбинациями:
23, 24, 25, 26, 27 – 5 раз.
Он не пожмет руку сам себе и первому другу, т.к. их рукопожатие мы уже посчитали. Аналогично рукопожатия каждого следующего приятеля будет уменьшаться на 1:
34, 35, 36, 37 – 4 раза пожал руку третий приятель;
45, 46, 47 – 3 раза четвёртый;
56, 57 – 2 раза пятый;
67 – и 1 раз шестой.
5. Посчитаем, сколько раз происходило рукопожатие каких-либо друзей. Получим
\(6 + 5 + 4 + 3 + 2 + 1 = 21\)
Ответ: 21.
ЗАДАЧИ ТРЕТЬЕГО ТИПА:
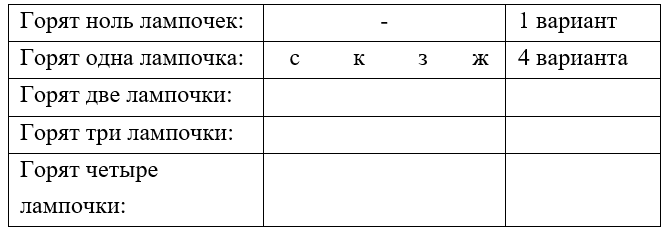
Есть лампочки четырех цветов – синего (с), красного (к), зеленого (з) и жёлтого (ж). Сколько существует комбинаций их включения? Вариант, когда все выключены тоже является одной из комбинаций.
1. Здесь нам снова неважен порядок включения лампочек, важно сколько и какие именно могут гореть одновременно. Будем рассматривать варианты включения разного количества лампочек.
2. Существует только один вариант, что лампочки выключены. Если лампочки включены по одной, то это может быть 4 варианта: с, к, ж или з:
3. Если горят две лампочки, то существует 6 таких комбинаций. Подобрать их можно так же, как мы находили пары в примере №2. Аналогично найдем уже тройки горящих лампочек, таких вариантов будет 4. И существует один вариант, когда горят все лампочки.
| Горят ноль лампочек: | - | 1 вариант |
|---|---|---|
| Горит одна лампочка: | с к з ж | 4 варианта |
| Горят две лампочки: | ск сз сж кз кж зж | 6 вариантов |
| Горят три лампочки: | скз скж кзж зжс | 4 варианта |
| Горят четыре лампочки: | скзж | 1 вариант |
4. Таким образом существует 16 различных вариантов одновременного включения лампочек, включая вариант, когда горят все лампочки и не горит не одной.
То есть мы нашли все возможные варианты подмножеств множества лампочек, включая пустое множество и само множество лампочек.
Комбинаторика
ПЕРЕСТАНОВКА:
Перестановка (\(\mathbf{P}_{\mathbf{n}}\)) – это конечное множество, в котором установлен порядок его элементов.
\(P_{n} = n!\)
где n – это количество элементов множества,
n! (эн факториал) = \(1 \bullet 2 \bullet 3 \bullet ... \bullet n\)
На полке стоят семь книг. Сколькими способами их можно расположить на полке?
Если у нас есть множество из семи книг и нам нужно перебрать все возможные варианты порядка их расположения, тогда используем формулу перестановки:
\(P_{7} = 7! = 1 \bullet 2 \bullet 3 \bullet 4 \bullet 5 \bullet 6 \bullet 7 = 5040\)
Ответ: 5040.
На полке стоят 9 книг, при этом среди них есть трёхтомник одного автора. Сколькими способами их можно расположить на полке, если книги трёхтомника должны находиться вместе, но в любом порядке?
1. При таком условии сначала представим трёхтомник как одну книгу. Тогда у нас не 9 книг, а 7. Тогда способов расположения таких книг существует 7! = 5040
2. При этом книги трёхтомника могут располагаться в разном порядке относительно друг друга. Таких комбинаций будет 3! = 6
3. А таком случае нужно перемножить перестановку трёхтомника относительно других книг и перестановку книг трёхтомника относительно друг друга:
\(P_{7} \bullet P_{3} = 7! \bullet 3! = 5040 \bullet 6 = 30240\)
Ответ: 30240.
Сколькими способами можно расположить между собой числа 0, 1, 2 и 3, если они не могут повторяться и число 2 не может быть первым?
1. Если у нас 4 элемента множества, тогда их перестановка равна:
\(P_{4} = 4! = 1 \bullet 2 \bullet 3 \bullet 4 = 24\)
2. При этом все комбинации, где число 2 стоит на первой позиции нужно исключить. Мысленно закрепим число 2 на первой позиции и начнем комбинировать оставшиеся элементы множества. Таким образом количество комбинаций, при которых число 2 стоит на первой позиции равно:
\(P_{3} = 3! = 1 \bullet 2 \bullet 3 = 6\)
3. Вычтем из количества всевозможных комбинаций количество неподходящих, получим:
\(P_{4}\ –\ P_{3} = 24\ –\ 6 = 18\)
Ответ: 18.
РАЗМЕЩЕНИЕ:
Например:
У нас есть множество \(\left\{ a,\ b,\ c,\ d \right\}\). Оно состоит из 4 элементов. Нам нужно найти количество всех возможных пар этих элементов. То есть будем выделять в этом множестве подмножества, содержащие только 2 элемента из 4. Чтобы найти количество этих пар, нужно посчитать размещение из 4 элементов по 2:
\(\boxed{A_{n}^{k} = n(n\ –1)(n\ –\ 2) \bullet ... \bullet (n\ –\ (k\ –\ 1))}\)
\(A_{4}^{2} = 4 \bullet 3 = 12\)
т.е. мы находим произведение двух натуральных множителей, наибольший из которых равен 4.
Эта формула преобразовывается в более ёмкую. Её удобнее использовать, когда мы говорим о большом количестве элементов:
\(\boxed{A_{n}^{k} = \frac{n!}{(n\ –\ k)!}}\)
\(A_{4}^{2} = \frac{4!}{(4\ –\ 2)!} = \frac{4!}{2!} = \frac{1 \bullet 2 \bullet 3 \bullet 4}{1 \bullet 2} = 3 \bullet 4 = 12\)
В общем смысле можно представить размещение как ситуацию, когда у нас есть множество из n элементов, мы будем выделять в нём подмножество из k элементов и считать именно их перестановки.
Если мы говорим о размещении n элементов по n – тогда размещение, по сути, становится перестановкой.
Сколько существует телефонных номеров, состоящих из 7 цифр, при этом первой цифрой номера не может быть 0 и цифры номера не повторяются?
1. Всего существует 10 цифр, а телефонный номер состоит только из 7 из них. Тогда мы говорим о размещении 10 элементов по 7. Найдем это размещение:
\(A_{10}^{7} = \frac{10!}{\left( 10–7 \right)!} = \frac{10!}{3!}\)
2. Но из такого количества телефонных номеров нужно исключить те, которые начинаются на 0. Таких размещений уже будет 9 по 6:
\(A_{9}^{6} = \frac{9!}{(9\ –\ 6)!} = \frac{9!}{3!}\)
3. Вычтем из всех размещений не подходящие условию:
\(A_{10}^{7}\ –\ A_{9}^{6} = \frac{10!\ –\ 9!}{3!} = \frac{9!(10\ –\ 1)}{3!} = 4 \bullet 5 \bullet 6 \bullet 7 \bullet 8 \bullet 9 \bullet 9 = 544320\)
Ответ: 544320.
СОЧЕТАНИЯ:
\(C_{n}^{k} = \frac{A_{n}^{k}}{P_{k}} = \frac{n!}{k!(n\ –\ k)!}\)
Например:
Если мы хотим выделить из множества \(\left\{ a,\ b,\ c,\ d \right\}\) все подмножества, которые включают в себя 2 элемента, то мы говорим о сочетании 4 элементов по 2. В таком случае, в отличие от размещения, не будут учитываться пары, в которые входят два одинаковых, но стоящих на разных позициях элемента. Например, пара ab – это то же самое, что пара ba. Перестановка элементов подмножества не играет роли, поэтому формула сочетания выглядит как размещение, деленное на перестановку k элементов.
Сколькими способами можно выбрать трёх дежурных из класса, в котором 25 человек?
Используем определение сочетания, т.к. нам важны лишь конкретные ученики, неважно в каком порядке мы их выбираем:
\(C_{25}^{3} = \frac{25!}{3!(25\ –\ 3)!} = \frac{25!}{3!22!} = \frac{23 \bullet 24 \bullet 25}{6} = 2300\)
Ответ: 2300.
В вазе стоят 8 красных и 5 белых роз. Нужно собрать букет из 3 красных роз и 2 белых. Сколькими способами это можно сделать?
1. Из-за того, что неважно, в каком порядке в букете стоят красные розы, а важно лишь их количество, тогда используем сочетания 8 красных роз по 3:
\(C_{8}^{3} = \frac{8!}{3!(8\ –\ 3)!} = \frac{8!}{3!5!} = \frac{1 \bullet 2 \bullet 3 \bullet 4 \bullet 5 \bullet 6 \bullet 7 \bullet 8}{3!1 \bullet 2 \bullet 3 \bullet 4 \bullet 5} = \frac{6 \bullet 7 \bullet 8}{6} = 56\)
2. Аналогично с белыми розами важны лишь возможные сочетания 5 красных роз по 2:
\(C_{5}^{2} = \frac{5!}{2!(5\ –\ 2)!} = \frac{5!}{2!3!} = \frac{4 \bullet 5}{2} = 10\)
3. Каждому выбору красных роз соответствует выбор белых, т.е. независимо от сочетания одного цвета выбирается сочетание другого. Поэтому перемножим эти сочетания:
\(C_{8}^{3} \bullet C_{5}^{2} = 56 \bullet 10 = 560\)
Ответ: 560.
БИНОМ НЬЮТОНА:
Мы знаем, что:
\(\left( a + b \right)^{1} = a + b\)
\(\left( a + b \right)^{2} = a^{2} + 2ab + b^{2}\)
\(\left( a + b \right)^{3} = a^{3} + 3a^{2}b + 3ab^{2} + b^{3}\)
\({(a + b)}^{4} = a^{4} + 4a^{3}b + 6a^{2}b^{2} + 4ab^{3} + a^{4}\)
И так далее по мере возрастания степени суммы меняются коэффициенты многочлена. Высчитать эти коэффициенты можно с помощью Бинома Ньютона, который является частным случаем сочетаний в комбинаторике.
\(\ {(a + b)}^{n} = C_{n}^{0}a^{n} + C_{n}^{1}a^{n\ –\ 1}b + C_{n}^{2}a^{n\ –\ 2}b^{2} + ... + C_{n}^{k}a^{n\ –k}b^{k} + ... + C_{n}^{n\ –\ 1}ab^{n\ –\ 1} + C_{n}^{n}b\)
Где n – натуральное число, коэффициенты \(С_{n}^{k}\) – это сочетания k по n, где k – порядковый номер коэффициента начиная с 0.
При этом для чисел a и b при одном коэффициенте сумма показателей степеней равна n.
ТРЕУГОЛЬНИК ПАСКАЛЯ
Из этой пирамиды чисел можно сразу узнавать коэффициенты для различных сумм, возведенных в степень.
Первая строчка пирамиды показывает нам, чему будут равны коэффициенты многочлена, равного сумме чисел в нулевой степени:
\(\left( a + b \right)^{0} = 1\)
Существует единственный коэффициент равный 1
У суммы чисел в первой степени будут коэффициенты, соответствующие второй строчке:
\(\left( a + b \right)^{1} = a + b\)
Коэффициенты при слагаемых равны 1 и 1
Коэффициенты привычного нам квадрата суммы равны 1, 2 и 1 соответственно:
\(\left( a + b \right)^{2} = a^{2} + 2ab + b^{2}\)
И так далее.
Можем взять, например, сразу узнать коэффициенты многочлена, равного 4-ой степени суммы чисел.
\({(a + b)}^{4}\)
Для этого посмотрим на 5-ую строчку треугольника.
Коэффициенты равны 1, 4, 6, 4 и 1 соответственно. Действительно, по Биному Ньютона, такими коэффициентами и будет обладать этот многочлен:
\({(a + b)}^{4} = a^{4} + 4a^{3}b + 6a^{2}b^{2} + 4ab^{3} + a^{4}\)

Содержание