Производные и пределы
Свойства функций
Зная свойства определённого вида функций, можно представить, как выглядит функция, как она себя ведет. Свойства помогают нам характеризовать функции.
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ЗНАЧЕНИЙ ФУНКЦИИ:
Область значений функции (E(y)) – это те значения функции, которые могут существовать для данной функции. Иначе говоря, это все возможные ординаты её точек.
Например:
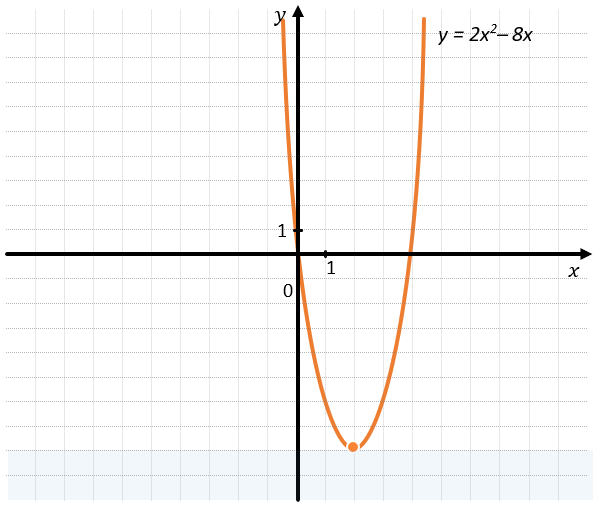
Рассмотрим область значений и определения функции \(y = 2x^{2}\ –\ 8x\). Построим график её функции:
Её область определения – это все рациональные числа, т.к. её точки могут бесконечно уходить влево и вправо.
А её область значений – это все значения ординат больше или равные, чем –8, т.к. ниже этой точки данный график не существует.
Получаем, что \(D(y) = R,\ E(y) = (–8; + \infty)\)
ОГРАНИЧЕННОСТЬ:
Например, парабола, ветви которой направлены вверх, всегда будет ограничена снизу, как бы мы её не перемещали по координатной плоскости. Она всегда будет иметь минимальное значение функции, ниже которой не опустится. А вот линейная функций нигде не ограничена, т.к. её график – бесконечная прямая.
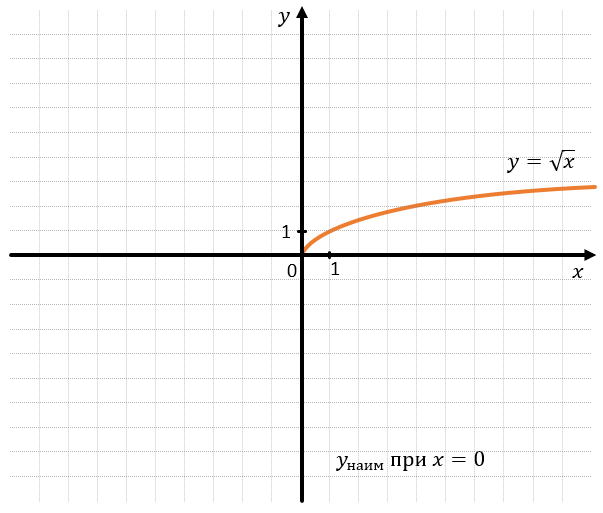
Примером ограниченной функции также является функция корня. Это функций ограничена сразу с нескольких сторон, т.к. может существовать только в одной четверти координатной плоскости:
НЕПРЕРЫВНОСТЬ:
Это свойство говорит нам о том, есть ли разрывы у функции.
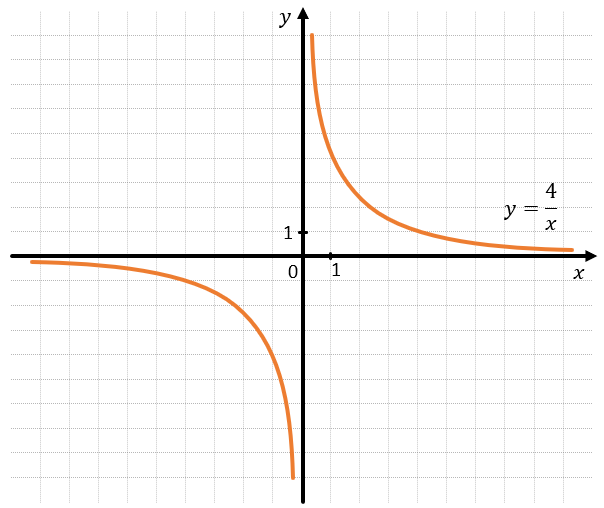
Прямая по которой проходит разрыв называется асимптотой.
Для графика функции \(y = \frac{k}{x}\) асимптотами являются прямые \(x = 0\) и \(y = 0\). На этих прямых данная функция не существует. Это влияет и на область допустимых значений, и на область допустимых определений:
МОНОТОННОСТЬ:
Функция возрастает – если функция «поднимается» слева направо.
Функция убывает – если функция «падает» слева направо.
Математическим язык можно сказать так:
Функция возрастает, если при возрастании значения абсцисс возрастает значение ординат её точек.
Функция убывает, если при возрастании значения абсцисс значение ординат её точек убывает.
Если функция на всем промежутке только возрастает или только убывает, тогда говорят, что функция монотонно возрастает или монотонно убывает.
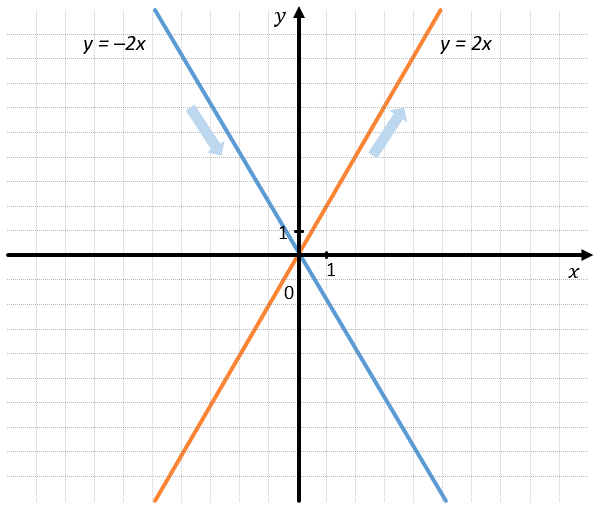
Например:
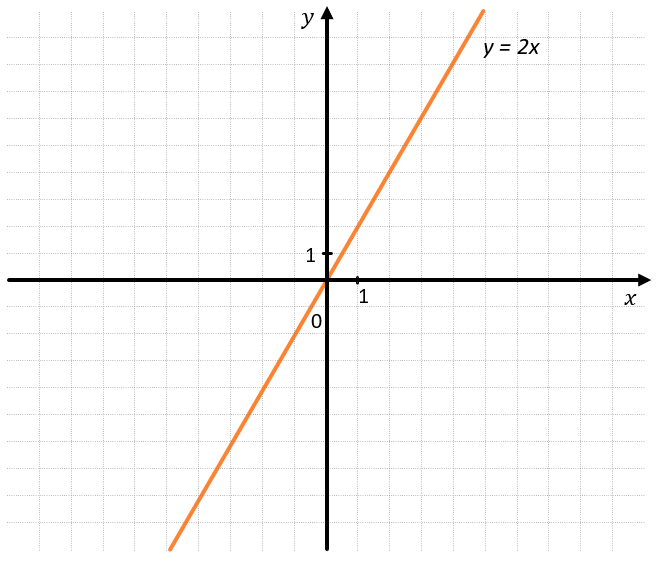
Можно сказать, что функция \(y = 2x\) монотонно возрастает, а функция \(y = \ –2x\) монотонно убывает.
Если функция на различных промежутках, то убывает, то возрастает, то такую функцию называют немонотонной и описывают её возрастание и убывание на конкретных промежутках.
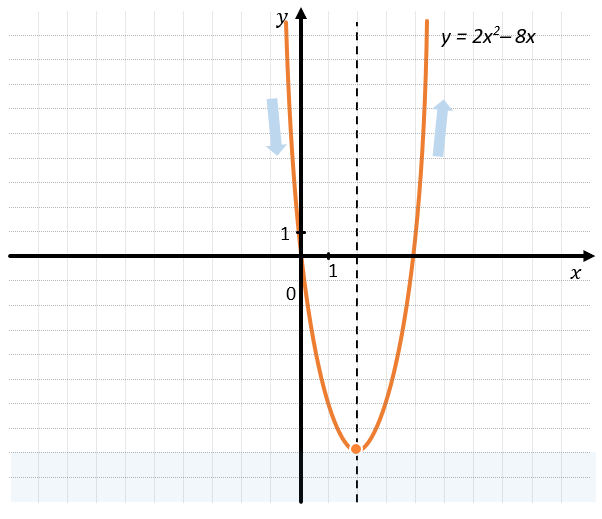
Например, любая квадратичная функция является немонотонной:
Можно характеризовать данную функцию на монотонность следующим образом:
Функция \(y = 2x^{2}–8x\) возрастает при \(x \in (–\infty;2)\) и убывает при \(x \in (2; + \ \infty).\)
ТОЧКИ ЭКСТРЕМУМА:
Если функция возрастает, а потом убывает, то точка между такими промежутками называется точкой максимума.
Если функция убывает, а потом возрастает, то точка между такими промежутками называется точкой минимума.
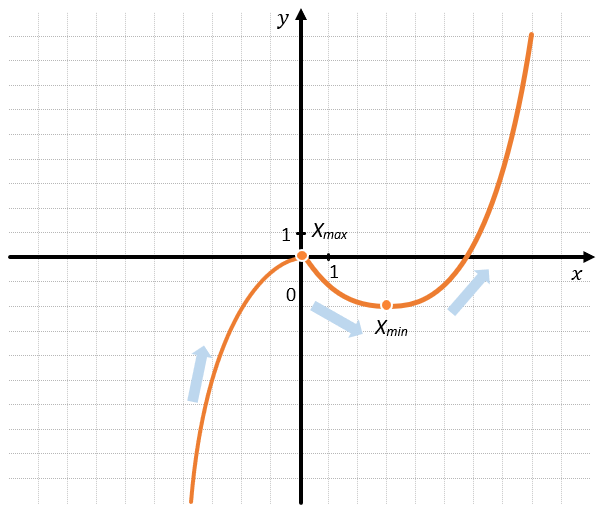
Например:
Данный график функций является немонотонным, и непрерывным, значит он имеет промежутки возрастания и убывания, между которые находятся точки экстремумов.
График возрастает при \(x \in (–\infty;0) \cup (3; + \infty)\) и убывает при \(x \in (0;3)\)
Точка минимум: \(x_{\min} = 3\)
Точка максимума: \(x_{\max} = 0\)
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИИ:
Наименьшее и наибольшее значение функции показывают, для каких аргументов значения функции наибольшие или наименьшие, например:
Это значит, что наименьшее значение наблюдается в конкретной точке x = 1. А наибольшее значение достигается, когда x стремить в положительную сторону бесконечно долго, в таких случаях говорят, что наибольшего значения функции не существует.
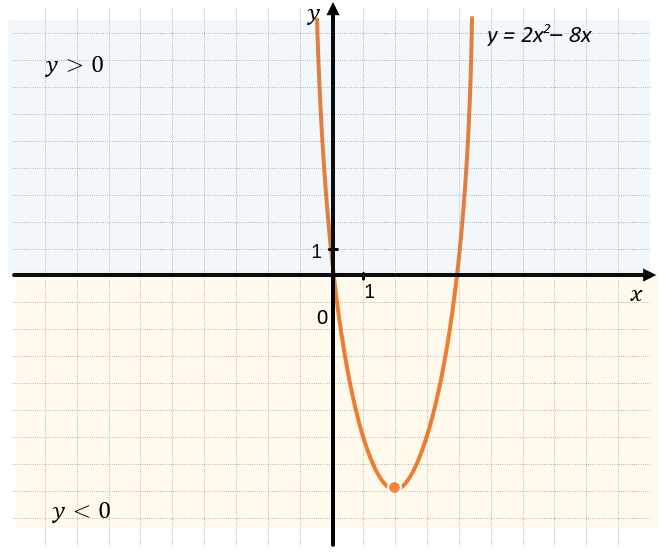
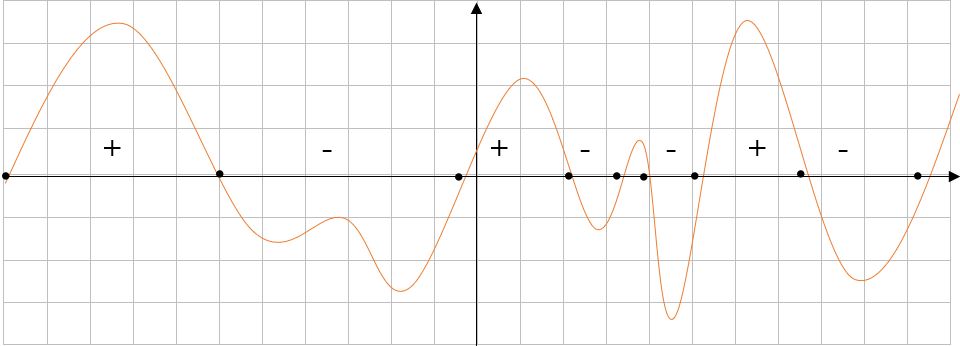
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:
Промежутки знакопостоянства показывают, на каких промежутках функция положительная, а на каких функция отрицательная.
Например:
\(y > 0\ при\ x \in \left( –\infty;0 \right) \cup \left( 4; + \infty \right)\)
\(y < 0\ при\ x \in (0;4)\)
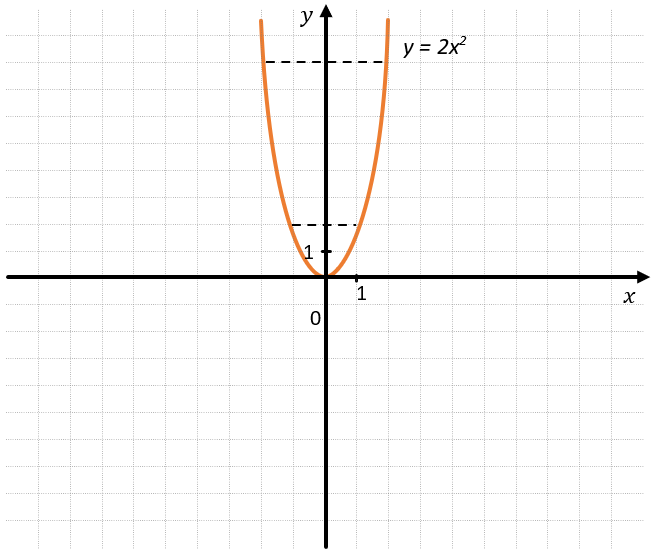
ЧЕТНОСТЬ ФУНКЦИИ:
Нечетная функция – это функция, симметричная началу координат. В таком случае \(f(–x) = –f(x).\)
Примером четной функции может служить косинус или парабола, вершина которой находится на оси Оу. В таком случае её ветви симметричны оси Оу:
Можно определить четность визуально: мы видим, что для \(x = 1\) и \(x = –1\ \)значение функции одинаково\(\ y = 2\ \)– следовательно функция четная.
Можно определить четность с помощью формул из определения четности и нечетности:
\(f\left( x \right) = f\left( –x \right)\)
\(y\left( 2 \right) = 2 \bullet 2^{2} = 2 \bullet 4 = 8\)
\(y\left( –2 \right) = 2 \bullet \left( –2 \right)^{2} = 2 \bullet 4 = 8\)
\(y(2) = y(–2) = 8\)
следовательно функция \(y\ = \ 2x^{2}\) четная.
Нечетной функцией является линейная функция, проходящая через начало координат, или функция обратной пропорциональности с асимптотами \(x = 0\) и \(y = 0:\)
Визуально нечетность выглядит как отражение графика на противоположную четверть – \(I\ \)отражается в \(\text{III}\) и наоборот и \(\text{II}\ \)отражается в \(\text{IV}\) и наоборот.
С помощью формулы аналогично можно определить и нечетность функции:
\(f\left( –x \right) = –f\left( x \right)\)
\(y\left( 3 \right) = 2 \bullet 3 = 6\)
\(y\left( –3 \right) = 2 \bullet \left( –3 \right) = \ –6\)
\(y(–3) = \ –y(3) = \ –6\)
следовательно функция нечетная.
Если для функции не соблюдается ни одно из этих условий четности, то ей называют ни четной, ни нечётной или функцией общего вида.
ПЕРИОДИЧНОСТЬ:
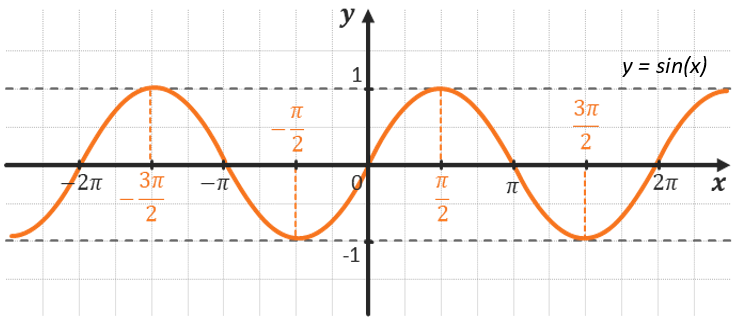
Примером периодичных функций являются тригонометрические функции.
Например, \(y = \sin(x)\) и \(y = \cos(x)\) имеют период\(\ 2\pi\), а функции \(y = \text{tg}(x)\ \)и \(y = \text{ctg}(x)\) имеют период π.
Различные графики имеют свой набор характеристик, поэтому, чтобы понять, как ведет себя конкретный график, нужно учитывать совокупность всех его свойств.
Смысл производной
Геометрический смысл производной
\(y = f^{'}\left( x_{0} \right)x - f^{'}\left( x_{0} \right) \bullet x_{0} + f\left( x_{0} \right)\)
\(f^{'}\left( x_{0} \right)\) — значение производной в точке \(x_{0}\)
\(x_{0} - \ \)координата самой точки
\(f\left( x_{0} \right)\) — значение функции в точке \(x_{0}\)
\(f^{'}\left( x_{0} \right) = k = tg\ \alpha\)
Отсюда можно сделать несколько выводов о том, как связаны значение производной и поведение функции:
1. Функция возрастает.
Если функция возрастает, но наклон касательной, проведенной в любой точке промежутка возрастания будет вправо, значит, ее коэффициент наклона положительный (k > 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.
\(Функция\ возрастает\ \Rightarrow f^{'}\left( x_{0} \right) > 0\)
2. Функция убывает.
Если функция убывает, но наклон касательной, проведенной в любой точке промежутка возрастания будет влево, значит, ее коэффициент наклона отрицательный (k < 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же отрицательна.
\(Функция\ убывает\ \Rightarrow f^{'}\left( x_{0} \right) < 0\)
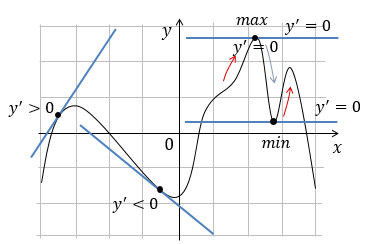
3. Экстремум.
Точки экстремума, отличаются тем, что в них функция и не возрастает, и не убывает. Если провести касательную в точке экстремума, то она будет строго горизонтальна, то есть ее наклон равен 0. А значит, и производная равна 0 (из соотношения между значением производной и коэффициентом наклона касательной выше).
\(Точка\ экстремума\ \Rightarrow f^{'}\left( x_{0} \right) = 0\)
Точка максимума
До неё функция возрастает, после него убывает. В точке максимума производная сменяет свой знак с плюса на минус.
\(Максимум:\ f^{'}\left( x_{0} \right)\ \mathbf{+ \ \Rightarrow \ -}\)
Точка минимума
До неё функция убывает, после него возрастает. В точке минимума производная сменяет свой знак с минуса на плюс.
\(Минимум:\ f^{'}\left( x_{0} \right)\mathbf{- \ \Rightarrow \ +}\)
Физический смысл производной
Допустим есть некоторая точка, которая двигается вдоль оси ОХ, и ее координата меняется со временем по закону \(x(t)\). Получается, что \(x\left( t \right)\) — это функция того, как меняется расстояние.
Мы знаем определение производной: это темп изменения функции. Если говорить про темп изменения расстояния, то можно догадаться, что это скорость.
То есть:
Чтобы найти скорость материальной точки, необходимо взять производную от функции координаты:
\(v\left( t \right) = x'(t)\)
Темп изменения скорости – это ускорение. Поэтому:
Чтобы найти ускорение, необходимо взять производную от функции скорости, то есть вторую производную от координаты:
\(a\left( t \right) = v^{'}\left( t \right) = x''(t)\)
Графическое применение производной
Мы приступаем к 7му заданию ЕГЭ. Один из способов решения заданий данной темы – это графический способ, который во многом облегчает жизнь ( учитывая, что данной теме выделено целое задание ЕГЭ, нельзя недооценивать его ). Сейчас мы рассмотрим, что могут нас попросить найти в данном типе заданий и разберем алгоритмы решения.
График функции
Если важен только знак производной:
-
Ищем промежутки возрастания/убывания
-
Делаем вывод о знаке производной
-
Ответ
Если важно значение производной:
-
Ищем промежутки возрастания/убывания
-
Строим касательную к графику в нужных точках
-
По её наклону делаем вывод о значении производной
-
Ответ
Если важно нулевое значение производной:
-
Находим на графике функции точки минимума/максимума
-
Делаем вывод согласно условиям задачи
-
Ответ
График производной функции
Если нужно найти точку, в которой функция принимает наибольшее/наименьшее значение:
-
Ищем промежутки, где график выше/ниже нуля
-
Делаем вывод о поведении функции на промежутке и в крайних точках
-
Ответ
Если нужно найти точку экстремума:
-
Рассматриваем точки пересечения графика с осью Ох
-
По смене знаков в этих точках определяем точки максимума и минимума
-
Ответ
Если нужно найти промежутки возрастания/убывания функции:
-
Ищем промежутки, на которых производная больше/меньше нуля
-
Ответ
График и уравнение касательной
Если дан график функции:
-
Ищем значение производной (по угловому коэффициенту касательной или через тангенс её наклона)
-
Ответ
Если дан график производной:
-
В условии находим угловой коэффициент касательной
-
Находим соответствующие значения на графике
-
Ответ
Уравнение функции и касательной
-
Приравниваем:
-
производную функции и угловой коэффициент касательной
-
значение функции и касательной в точке касания
-
Составляем и решаем систему уравнений:
\(\left\{ \begin{matrix} f’(x_{1}\ ) = a \\ \text{\ \ \ f}\left( x_{1} \right) = ax_{1} + b \\ \end{matrix} \right.\ \)
-
Ответ
Первообразная
Если дан график \(f(x)\) с двумя границами \(\lbrack a;\ b\rbrack\) и явный вид первообразной \(F(x) = \ \ldots\ \ \)
-
Подставляем граничные точки в первообразную и находим площадь под графиком \(S = F(b) - F(a)\ \)
Если дан простой график и нужно найти \(F(b) - F(a)\)
-
Ищем площадь под графиком по клеточкам в интервале \(\lbrack a;b\rbrack\) и находим\(\ F(b) - F(a) = S\)
Если дан график функции или первообразной
-
Пользуемся определением первообразной \(F’(x) = f(x)\)
Экстремумы
Тема дифференциалы все усложняется. Сейчас посмотри уже 12 задание, где графическое решение будет только маленьким кусочком решения.
-
Точка экстремума (координата, геопозиция)– значение аргумента (x)
-
Экстремум (насколько высокая гора / низкая впадина) – значение функции (y)
Задание № 12
Найти точку экстремума (x) или экстремум (y).
Найти наибольшее/наименьшее значение функции на \(\lbrack a;b\rbrack.\)
Нахождение минимума/максимума
-
Находим производную.
-
Находим точки экстремума (приравниваем производную к нулю и решаем уравнение).
-
Находим знаки производной между точками экстремума, делаем вывод по знакам.
-
Для нахождения значения функции подставляем найденный x в функцию.
Проверка значений производной:
-
Подставляем наиболее удобные числа.
-
Проверяем минимальное необходимое количество промежутков.
-
Единственную точку экстремума можно не проверять.
Нахождение наибольшего/наименьшего значения на \(\mathbf{\lbrack a;\ b\rbrack}\)
-
Находим производную, приравниваем к нулю и находим точки экстремума.
-
Считаем ИСХОДНУЮ функцию в:
-
Начале промежутка
-
Конце промежутка
-
В экстремумах, лежащих в \(\lbrack a;\ b\rbrack\) (если есть).
-
Выбираем нужное значение. В ответ – значение ФУКНЦИИ.
Альтернативный способ решения
Если функция \(f\left( x \right)\) всегда возрастает, то наибольшее / наименьшее значение функции \(f(g\left( x \right))\) будет достигаться там же, где и наибольшее / наименьшее значение функции \(g\left( x \right)\).
| Всегда возрастающие функции: | Всегда убывающие функции: |
|---|---|
| \(\mathbf{f}\left( \mathbf{x} \right)\mathbf{=}\sqrt{\mathbf{x}}\) | \(f\left( x \right) = \log_{x}a,\ при\ 0 < a < 1\) |
| \(\mathbf{f}\left( \mathbf{x} \right)\mathbf{=}\mathbf{\log}_{\mathbf{a}}\mathbf{x}\mathbf{,\ при\ a > 1}\) | \(f\left( x \right) = a^{x},\ при\ 0 < a < 1\) |
| \(\mathbf{f}\left( \mathbf{x} \right)\mathbf{=}\mathbf{a}^{\mathbf{x}}\mathbf{,\ при\ a > 1}\) |
Найдите точку минимума функции \(y = x^{3} - 27x + 15\)
Решение:
Найдем производную и приравняем к 0:
\({3x}^{2} - 27 = 0\)
\({3x}^{2} = 27\)
\(x^{2} = 9\)
\(x_{1,2} = \pm 3\)
\(\text{\ x}\)
-3 3
Нас интересует точка минимума, значит выбираем точку, через которую знак с - меняется на +. Выбираем -3
Ответ: -3
Правила дифференцирования
Название производной происходит от слова «произведенная», т.е. образованная от другой величины. Производная характеризует темп изменения функции.
Процесс определения производной какой-либо функции называется дифференцированием. Если говорить совсем просто, то для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию.
Формулы нахождения производных основных функций
Число, степенная функция, функция с коэффициэнтом
|
Функция Формула |
Пример |
|---|---|
|
Число \(c' = \ 0\) |
\(7' = \ 0\) Важно! \((ln\ 7)'\ = 0\) \(\pi^{'} = 0\) Так как это число, а не функция |
|
Степенная функция \(\left( x^{n} \right)^{'} = \ n \bullet \ x^{n - 1}\) |
\(\left( x^{7} \right)^{'} = 7 \bullet x^{7 - 1} = 7 \bullet x^{6}\) |
|
Частный случай — квадратный корень \((\sqrt{x})'\ = \frac{1}{2\sqrt{x}}\) |
Вывод формулы: \(\left( \sqrt{x} \right)^{'} = \left( x^{\frac{1}{2}} \right)^{'} = \frac{1}{2}x^{\frac{1}{2} - 1} = \frac{1}{2}x^{- \frac{1}{2}} = \frac{1}{2\sqrt{x}}\) |
|
Частный случай — обратная функция \(\left( \frac{1}{х} \right)^{'} = - \frac{1}{x^{2}}\) |
Вывод формулы: \(\left( \frac{1}{х} \right)^{'} = \left( x^{- 1} \right)^{'} = - 1 \bullet x^{- 1 - 1} = - \frac{1}{x^{2}}\) |
|
Производная от функции, умноженной на коэффициент \(\left( c \bullet f\left( x \right) \right)^{'} = c \bullet f'(x)\) |
\(\left( 7x \right)^{'} = 7 \bullet x^{'} = 7 \bullet 1 = 7\) \(\left( 3x^{7} \right)^{'} = 3 \bullet {(x}^{7})' = 3 \bullet 7 \bullet x^{7 - 1} = 21 \bullet x^{6}\) |
Производная от показательно – степенной и логарифмической функций
|
Показательно-степенная функция \(\left( a^{x} \right)^{'} = a^{x} \bullet \ln a\) |
\(\left( 7^{x} \right)^{'} = 7^{x} \bullet \ln 7\) |
|---|---|
|
Частный случай показательно-степенной функции — основание е (экспонента) \(\left( e^{x} \right)^{'} = e^{x}\) |
Вывод формулы: \(\left( e^{x} \right)^{'} = e^{x} \bullet \ln{e = e^{x} \bullet 1 = e^{x}}\) |
|
Логарифмическая функция \({{(log\ }_{a}x)' = \frac{1}{x \bullet \ln a}}_{\ }\) |
\({(\log\ }_{7}x)' = \frac{1}{x \bullet \ln 7}\) |
|
Частный случай логарифмической функции —с натуральным логарифмом (основание логарифма — е) \((\ln x)' = \frac{1}{x}\) |
Вывод формулы: \(\left( \ln x \right)^{'} = \frac{1}{x \bullet \ln e} = \frac{1}{x \bullet 1} = \frac{1}{x}\) |
Производная от тригонометрических функций
|
Синус \((\sin{x)' = cos\ x}\) |
- |
|---|---|
|
Косинус \((\cos{x)' = - sin\ x}\) |
- |
|
Тангенс \((\text{tg}{x)' = \frac{1}{\cos^{2}x\ }}\) |
Вывод формулы: \(\left( \text{tg}x \right)^{'} = \left( \frac{\sin x}{\cos x} \right)^{'} = \frac{\left( \sin x \right)^{'} \bullet \cos x - \sin x \bullet \left( \cos x \right)^{'}}{\cos^{2}x} = \frac{\cos x \bullet \cos x - \sin x \bullet ( - \sin{x)}}{\cos^{2}x} = \frac{\cos^{2}x + \sin^{2}x}{\cos^{2}x} = \frac{1}{\cos^{2}x\ }\) |
|
Котангенс \((\text{ctg}{x)' = - \frac{1}{\sin^{2}x\ }}\) |
Вывод формулы: \(\left( \text{ctg}x \right)^{'} = \left( \frac{\cos x}{\sin x} \right)^{'} = \frac{\left( \cos x \right)^{'} \bullet \sin x - \cos x \bullet \left( \sin x \right)^{'}}{\sin^{2}x} = \frac{- \sin x \bullet \sin x - \cos x \bullet \cos x}{\sin^{2}x} = \frac{{- \sin}^{2}x - \cos^{2}x}{\sin^{2}x} = \frac{- 1 \bullet \cos^{2}x + \sin^{2}x}{\sin^{2}x\ } = - \frac{1}{\sin^{2}x\ }\) |
Производная от обратных тригонометрических функций
|
Арксинус \((\arcsin{x)' = \frac{1}{\sqrt{1 - x^{2}}}}\) |
Арктангенс \((\text{arctg}{x)' = \frac{1}{1 + x^{2}\ }}\) |
|---|---|
|
Арккосинус \(({\text{arc}\cos}{x)' = - \frac{1}{\sqrt{1 - x^{2}}}}\) |
Арккотангенс \((\text{arcctg}{x)' = - \frac{1}{1 + x^{2}\ }}\) |
Производная от суммы, произведения и частного функций
|
Сумма функций \(\left( f\left( x \right) + g\left( x \right) \right)^{'} = f'\left( x \right) + g'\left( x \right)\) |
\(\left( 7^{x} + 7 \right)^{'} = {(7^{x})}^{'} + 7' = 7^{x} \bullet \ln 7\) |
|---|---|
|
Произведение функций \(\left( f\left( x \right) \bullet g(x) \right)^{'} = f^{'}\left( x \right) \bullet g\left( x \right) + f(x) \bullet g'\left( x \right)\) |
\(\left( x^{7} \bullet \cos x \right)^{'} = \left( x^{7} \right)^{'} \bullet \cos x + x^{7} \bullet \left( \cos x \right)^{'} = 7 \bullet x^{6} \bullet \cos{x + x^{7} \bullet ( - \sin{x)}} = 7 \bullet x^{6} \bullet \cos{x - x^{7} \bullet \sin x}\) |
|
Частное функций \(\left( \frac{f\left( x \right)}{g\left( x \right)} \right)^{'} = \frac{f^{'}(x) \bullet g\left( x \right) - f(x) \bullet g'\left( x \right)}{g^{2}\left( x \right)}\) |
\(\left( \frac{x^{7}}{\cos x} \right)^{'} = \frac{\left( x^{7} \right)' \bullet \cos x - x^{7} \bullet (\cos x)'}{\cos^{2}x} = \frac{7 \bullet x^{6} \bullet \cos{x - x^{7} \bullet ( - \sin{x)}}}{\cos^{2}x} = \frac{7 \bullet x^{6} \bullet \cos{x + x^{7} \bullet \sin x}}{\cos^{2}x}\) |
Сложная функция
| \(\cos\text{x\ }\) — простая функция | \(\cos\sqrt{x}\) — сложная функция: внутри функции косинуса стоит функция корня |
|---|---|
| \(e^{x}\)— простая функция | \(e^{2x - 7}\) — сложная функция: внутри показательно-степенной функции стоит линейная функция\(\ 2x - 7\) |
\((f\left( g\left( x \right) \right)' = f'(g) \bullet g'(x)\)
Что она означает: мы берем производную от внешней функции, сохраняя ее аргумент таким, какой он был (то есть сохраняем ту функцию, которая стояла внутри), а потом умножаем ее на производную внутренней функции.
\(\cos{(3x - 2)}\)
Косинус — внешняя функция, сначала берем производную от нее
\(f^{'}\left( g \right) = (\cos{(3x - 2))' =} - \sin{(3x - 2)}\)
Обратите внимание, что внутренняя функция g = 3x – 5 не изменилась, её мы не трогаем. Отдельно находим от нее производную.
\(g^{'}\left( x \right) = \left( 3x - 2 \right)^{'} = 3\)
Теперь перемножим функции по формуле:
\({(cos}{(3x - 2))' =} - \sin{(3x - 2)} \bullet 3\)
\(\log_{12}{(x^{2})}\)
Внешняя функция логарифмическая, сначала берем производную от нее
\(f^{'}\left( g \right) = (\log_{12}{(x^{2}))' =}\frac{1}{x^{2} \bullet \ln 12}\)
Внутренняя функция g = x² пока не изменилась. Отдельно находим от нее производную:
\(g^{'}\left( x \right) = \left( x²\ \right)^{'} = 2x\)
Теперь перемножим функции по формуле:
\({(\log_{12}\left( x^{2} \right))}^{'} = \frac{2x}{x^{2} \bullet \ln 12}\)
\(4^{x^{2} - 2x + 7}\)
Внешняя функция логарифмическая, сначала берем производную от нее
\(f^{'}\left( g \right) = \left( 4^{x^{2} - 2x + 7} \right)^{'} = 4^{x^{2} - 2x + 7} \bullet \ln 4\)
Внутренняя функция g = x² пока не изменилась. Отдельно находим от нее производную:
\(g^{'}\left( x \right) = \left( x^{2} - 2x + 7\ \right)^{'} = 2x - 2\)
Теперь перемножим функции по формуле:
\({(4^{x^{2} - 2x + 7})}^{'} = 4^{x^{2} - 2x + 7} \bullet \ln 4 \bullet (2x - 2)\)
Анализ функций
\(f^{'}\left( x_{0} \right) = tg\ \alpha = k\)
Отсюда можно сделать несколько выводов о том, как можно анализировать функцию с помощью производной:
1. Функция возрастает.
Если функция возрастает, но наклон касательной, проведенной в любой точке промежутка возрастания будет вправо, значит, ее коэффициент наклона положительный (k > 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же положительна.
\(Функция\ возрастает\ \Rightarrow f^{'}\left( x_{0} \right) > 0\)
2. Функция убывает.
Если функция убывает, но наклон касательной, проведенной в любой точке промежутка возрастания будет влево, значит, ее коэффициент наклона отрицательный (k < 0). Из соотношения между значением производной и коэффициентом наклона касательной можно сказать, что производная будет так же отрицательна.
\(Функция\ убывает\ \Rightarrow f^{'}\left( x_{0} \right) < 0\)
3. Экстремум.
Точки экстремума, отличаются тем, что в них функция находится в пиковом значении, она и не возрастает, и не убывает. Если провести касательную в точке экстремума, то она будет строго горизонтальна, то есть ее наклон равен 0. А значит, и производная равна 0 (из соотношения между значением производной и коэффициентом наклона касательной выше).
\(Точка\ экстремума\ \Rightarrow f^{'}\left( x_{0} \right) = 0\)
Максимум.
До него функция возрастает, после него убывает. В максимуме производная сменяет свой знак с плюса на минус.
\(Максимум:\ f^{'}\left( x_{0} \right)\ + \ \Rightarrow \ -\)
Минимум.
До него функция убывает, после него возрастает. В минимуме производная сменяет свой знак с минуса на плюс.
\(Максимум:\ f^{'}\left( x_{0} \right) - \ \Rightarrow \ +\)
Отсюда можно вывести общий порядок действий при анализе функций:
-
Находим производную от функции.
-
Находим точки экстремума: приравниваем производную к нулю и решаем уравнение.
-
Определяем знаки производной между точками экстремума.
-
Если в точке знак производной меняется с плюса на минус — это максимум.
-
Если в точке знак производной меняется с минуса на плюс — это минимум.

Содержание