Проценты и задачи на % в страховании и экономике
Текстовые задачи на проценты
Для быстрого и верного решения задач на проценты нужно понимание сути процента, умение считать проценты и внимательно читать условие.
С процентами нам постоянно приходится сталкиваться в повседневной жизни. «Скидка 30%», «Кредит без процентов за 5 минут», «Арендная плата выросла на 12%» - со всех сторон на нас сыплются рекламные слоганы и призывы. Но что же значит слово «проценты»? И как ими оперировать?
Проценты являются удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываются на них.
Что такое процент?
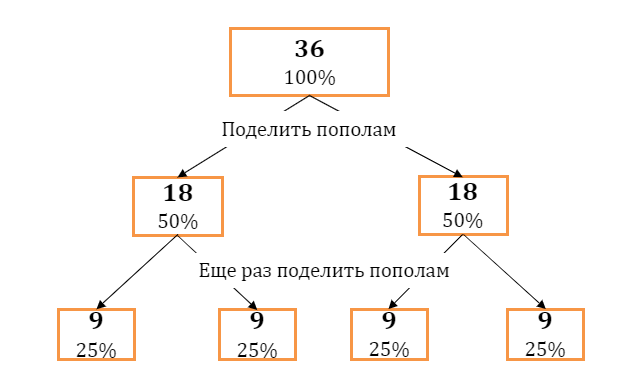
Процент – это всегда доля какого-то числа.
100% - все число
50% - половина
25% - четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Один процент – одна сотая доля.
Нахождение процента через деление на 100:
1. Делим изначальное число на 100 (таким образом получаем величину 1 процента от числа).
2. Умножаем на нужное нам количество процентов.
Например, чтобы найти 25% от 200, нужно:
-
Сначала найти, сколько составляет 1% от 200:
\(200:100 = 2\)
2.Умножить полученное значение на нужное нам количество процентов, то есть на 25:
\(2 \cdot 25 = 50\)
Нахождение процента через умножение на десятичную дробь:
Принцип действия тот же, однако 2 действия объединяем в одно – умножаем исходное число сразу на дробь.
1. Превращаем процент в дробь (отсчитываем 2 символа справа и ставим запятую), например:
\(115\% = 1,15\)
\(82\% = 0,82\)
\(7\% = 0,07\)
\(25\% = 0,25\)
2. Умножаем число на полученную дробь:
25% от \(200 = 200 \cdot 0,25 = 50\)
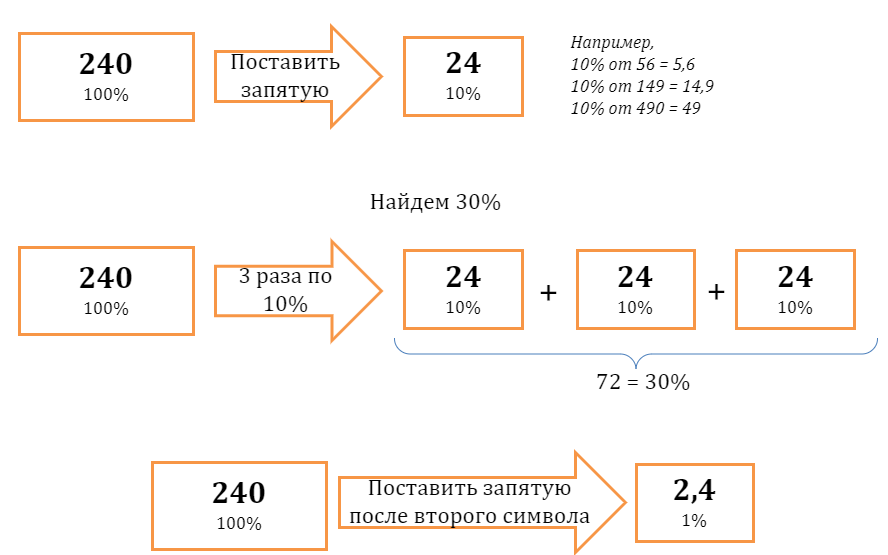
Нахождение процента упрощённым способом «по кубикам»
Пользуясь правилом перевода процента в десятичную дробь, а затем – правилом перевода десятичной дроби в обыкновенную, можем вывести стандартные соотношения:
\(1\% = \frac{1}{100}\)
\(\ 10\% = \frac{1}{10}\)
\(\ 20\% = \frac{1}{5}\)
\(\ 25\% = \frac{1}{4}\)
\(\ 50\% = \frac{1}{2}\)
\(\ 75\%\ = \frac{3}{4}\)
Тогда работу с дробями мы можем заменить простым умножением или делением.
Например, чтобы найти 25% от 200, можно 200 поделить на 4 и получить 50.
Итак, пользуясь методом кубиков всегда можно найти 50%, 25%, а также 1%,10% и 20%. Например:
Для вычисления 1% нужно поставить запятую после второго символа, а для нахождения 10% поставить запятую после первого символа.
Далее, чтобы получить иной процент, нужно умножить полученное значение на нужное количество процентов. Например:
Как работать с процентами в текстовых задачах?
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом – соответствующие проценты.
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно.
Например, если известно, что всего на прилавке имеется 200 груш, и нужно найти, сколько груш составляет 1%.
Составляем пропорцию:
200 груш – 100 %
x груш – 1 %
Пользуемся правилом произведения накрест лежащих значений:
\(200 \cdot 1 = x \cdot 100\)
Выражаем искомую величину:
\(x = \frac{200 \cdot 1}{100} = 2\)
Получаем готовое соотношение:
200 груш – 100 %
2 груши – 1 %
Итак, 1% от всего количества составляет 2 груши.
Или другая задача: известно, что 20% от всего количества составляет 40 груш. Сколько всего груш на прилавке?
Составляем пропорцию:
x груш – 100 %
40 груш – 20 %
Пользуемся правилом произведения накрест лежащих значений:
\(x \cdot 20 = 40 \cdot 100\)
Выражаем искомую величину:
\(x = \frac{40 \cdot 100}{20} = 200\)
Получаем готовое соотношение:
200 груш – 100 %
40 груш – 20 %
Итак, 100% — это 200 груш.
Видим, что пропорция отражает зависимость величин, по-другому это можно записать в виде двух дробей:
\(\frac{200}{2} = \frac{100}{1}\) или \(\frac{200}{40} = \frac{100}{20}\)
Сложные проценты
Билет на концерт стоил 1000 рублей. За месяц до концерта цена билета вырастет на 10%, а перед входом можно будет купить билет еще на 10% дороже. Сколько будет стоить билет перед входом на концерт?
1. Понятно, что, если билет подорожал на 10%, значит надо к изначальной стоимости прибавить 10% от неё же. То есть:
\(1000 + 1000 \bullet \frac{10}{100}\)
Вынесем изначальную стоимость за скобки:
\(1000(1 + 0,1) = 1000 \bullet 1,1 = 1100\)
Последнее действие можно представить как умножение изначальной стоимости сразу на 110%. Действительно, если у нас было 100% и мы прибавили к ним еще 10%, то в итоге и получается 110% от изначальной цены.
2. Но перед входом цена будет дороже еще на 10%:
\(1100(1 + 0,1) = 1100 \bullet 1,1 = 1210\)
Такое неоднократное повышение чего-либо на одинаковый процент несколько раз – и есть сложные проценты.
Ответ: 1210.
Выведем общую формулу сложного процента:
1. Обозначим начальную стоимость билета за \(S\), а процент, на которой цена вырастет, за\(\ r\).
\(S = 1000\)
\(r = 10\)
2. Тогда вот каким образом цена поменяется за месяц до концерта:
\(S + S \bullet \frac{r}{100} = S(1 + \frac{r}{100})\)
3. Перед концертом эта стоимость вырастет в то же количество процента и станет равна:
\(S(1 + \frac{r}{100}) \bullet (1 + \frac{r}{100})\)
4. Умножение на одинаковую скобку несколько раз можем записать как скобку в квадрате:
\(S\left( 1 + \frac{r}{100} \right)^{2}\)
Таким образом
\(S\left( 1 + \frac{r}{100} \right)^{n}\)– это формула сложного процента.
где \(S\) – изначальная стоимость, \(r\ \)– процент изменения стоимости, \(n\) – количество раз её изменения.
Экономические задачи. Вклады
Задачи на вклады – это блок экономических задач в реальной математике. Для решения этих задач необходимо понимать суть некоторых экономических операций, которые в свою очередь тесно связаны с формулой сложного процента.
ЧТО ТАКОЕ ВКЛАД:
Суть вклада в том, что человек отдает банку свои деньги на хранение. Это можно делать для разных целей, например, чтобы накопить на что-то. Иногда банк предлагает такой вклад, с которого вы не сможете снять свои же деньги на протяжении заранее оговорённого времени. Так вы точно не потратите ничего лишнего.
Итак, люди кладут деньги в банк, чтобы получить с них проценты, потому что банк платит людям за то, что те доверяют банку и позволяют ему на некоторый период пользоваться этими деньгами. Банк как бы занимает деньги, а потом отдает их с процентами.
При этом существуют некоторые условия начисления процента. Он чаще всего накладывается не на ту сумму, которую вы положили в самом начале, а рассчитывается каждый день, месяц или год на ту сумму, которая фактически лежит на вкладе. То есть если вы доложите на вклад с деньгами еще столько же, то через определенный расчётный период вам начислят процент на бόльшую сумму, а следовательно ваша прибыль со вклада вырастет.
МАТЕМАТИЧЕСКИЙ СМЫСЛ ВКЛАДА:
Так как каждый последующий год процент начисляется не на исходную сумму, а на ту сумму, которая уже лежит на вкладе, тогда процент может начисляться на вклад с уже начисленным процентом. Здесь нам пригодится формула сложного процента:
\(S_{n} = S_{0}\left( 1 + \frac{r}{100} \right)^{n}\)
\(где\ S - сумма\ на\ вкладе\ за\ \text{n\ }месяцев\ или\ лет\)
\(S_{0} - сумма,\ положенная\ на\ вклад;\)
\(r - процентная\ ставка\ вклада\)
\(n - расчетный\ перирод,\ количество\ \)
\(месяцев\ или\ лет,\ на\ которое\ расчитывается\ вклад\)
Алексей хочет в начале года открыть вклад на 100 000 рублей под 10% годовых. Процент начисляется в начале каждого года, начиная со второго. Через какое минимальное количество сколько лет Алексею можно снять деньги с вклада, чтобы сумма на нём была больше 133 000?
СПОСОБ 1
Найдем, чему будет равна сумма на вкладе через 1 год, через 2 года и т. д., пока сумма не станет больше 130 000.
-
Через один год на вкладе будет лежать сумма:
\(S_{1} = 100\ 000 \bullet \left( 1 + \frac{10}{100} \right) = 100\ 000 \bullet 1.1 = 110\ 000\)
-
Через два года процент будет налагаться уже на полученную сумму:
\(S_{2} = 110\ 000 \bullet 1.1 = 121\ 000\)
-
Аналогично наложим проценты на второй год, чтобы получить третий:
\(S_{3} = 121\ 000 \bullet 1.1 = 133\ 100\)
-
Видим, что, если Алексей заберет деньги после трёх лет, он снимет сумму, превышающую 133 000 рублей. Запишем ответ.
Ответ: 3.
СПОСОБ 2
Мы можем сразу использовать формулу сложного процента и составить неравенство, не рассчитывая каждый год по отдельности.
-
Запишем все известные нам данные в формулу сложного процента. Так как нам нужно найти количество лет, за которое на вклад будет накладываться процент, \(n\) будет неизвестной искомой величиной:
\(S_{n} = 100\ 000\left( 1 + 0,1 \right)^{n}\)
-
При этом у нас есть условие, что через некоторое количество лет, когда Алексей снимет деньги, сумма на вкладе будет больше 133 000, а значит\(\text{\ S}_{n} > 133\ 000\). Составим неравенство:
\(100\ 000{\bullet 1,1}^{n} > 133\ 000\)
-
Решим неравенство относительно \(n\):
\({1,1}^{n} > 1,33\)
Возведем 1,1 по порядку во вторую, третью и т. д. степень:
\({1,1}^{2} = 1,21\)
\({1,1}^{3} = 1,331\)
То есть, чтобы \({1,1}^{n}\) должно быть больше, чем 1,33, \(n\) должно быть равно 3:
\({1,1}^{3} > 1,33\)
Значит Алексей должен снять деньги минимум через три года, чтобы сумма на вкладе была больше 133 000. Запишем ответ.
Ответ: 3.
Анастасия открыла вклад на 100 000 на три года под 20% годовых. Процент начисляется в начале каждого года, начиная со второго. Сколько денег будет лежать на вкладе Анастасии через три года, если в середине второго года она снимет 10 000 ?
-
Составим таблицу, отображающую сумму на вкладе в начале и в конце каждого года:
| Год | Начало года | Конец года |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
В начале первого года процент не накладывается. При этом до начала второго года сумма на вкладе не поменяется. Запишем это в таблицу:
| Год | Начало года | Конец года |
|---|---|---|
| 1 | 100 000 | 100 000 |
| 2 | ||
| 3 |
-
Уже в начале второго года на сумму на вкладе начислится 20%:
| Год | Начало года | Конец года |
|---|---|---|
| 1 | 100 000 | 100 000 |
| 2 | \(100\ 000\ \bullet \ 1,2\ = \ 120\ 000\) | |
| 3 |
При этом в задаче есть условие – Анастасия снимет со вклада 10 000 в середине второго года. Значит, к концу второго года вклад уменьшится на эту сумму:
| Год | Начало года | Конец года |
|---|---|---|
| 1 | 100 000 | 100 000 |
| 2 | \(100\ 000\ \bullet \ 1,2\ = \ 120\ 000\) | \(120\ 000\ –10\ 000 = 110\ 000\) |
| 3 |
-
В начале третьего года снова на оставшуюся сумму наложится 20%:
| Год | Начало года | Конец года |
|---|---|---|
| 1 | 100 000 | 100 000 |
| 2 | \(100\ 000\ \bullet \ 1,2\ = \ 120\ 000\) | \(120\ 000\ –10\ 000 = 110\ 000\) |
| 3 | \(110\ 000\ \bullet \ 1,2\ = \ 132\ 000\) |
За год вклад никак не поменяется, значит, в конце третьего года на вкладе так и останется 132 000 рублей:
| \(\mathbf{Год}\) | Начало года | Конец года |
|---|---|---|
| 1 | 100 000 | 100 000 |
| 2 | \(100\ 000\ \bullet \ 1,2\ = \ 120\ 000\) | \(120\ 000\ –10\ 000 = 110\ 000\) |
| 3 | \(110\ 000\ \bullet \ 1,2\ = \ 132\ 000\) | 132 000 |
Запишем ответ.
Ответ: 132 000.
Известно, что вклад составляет целое количество миллионов рублей. В конце каждого года вклад увеличивается на 25% по сравнению с началом года. На какую сумму нужно открыть вклад, чтобы через два года на нём лежало больше 6 миллионов рублей?
-
Составим уравнение по формуле сложного процента. Мы не знаем, чему равна изначальная сумма, положенная на вклад, но мы знаем процентную ставку и количество лет:
\(S_{2} = S_{0} \bullet \left( 1 + 0,25 \right)^{2}\)
-
При этом сумма через два года должна быть больше 6 миллионов, тогда получаем неравенство:
\(S_{0} \bullet \left( 1 + 0,25 \right)^{2} > 6\)
-
Решим это неравенство относительно \(S_{0}\):
\(S_{0} > \frac{6}{{1,25}^{2}}\)
Представим 1,25 как дробь \(\frac{5}{4}\):
\(S_{0} > \frac{6}{\frac{5^{2}}{4^{2}}}\)
\(S_{0} > \frac{6 \bullet 16}{25}\)
\(S_{0} > \frac{96}{25}\)
-
Если \(S_{0}\) по условию равно целому количеству миллионов, определим. Между какими целыми числами находится дробь \(\frac{96}{25}\). Так как \(S_{0}\) должно быть больше этой дроби, выберем большее целое число:
\(3 < \frac{96}{25} < 4\)
Значит \(S_{0} = 4\) млн. Запишем ответ.
Ответ: 4.
Экономические задачи. Кредиты
Задачи на кредиты – наиболее часто встречающиеся экономические задачи. Здесь вы можете встретить различные схемы возврата кредита одинаковыми и разными платежами. Для решения задач на кредиты нужно понимать, что это такое, как действуют операции с кредитами и как они связаны с формулой сложного процента.
ЧТО ТАКОЕ КРЕДИТ:
Кредит происходит от латинского слова «доверие». Это такая экономическая операция, при которой банк отдает вам на время свои деньги, рассчитывая, что вы вернете их с процентами за то, что имели возможность их использовать. Кредит похож на вклад, только при вкладе банк платит вам за пользование вашими деньгами, а при кредите вы платите банку за пользование его деньгами.
Проценты по кредиту начисляются спустя определенный расчётный период – каждый месяц или год. При этом они почти всегда начисляются на оставшийся долг, то есть если за некоторое время вы успели закрыть часть долга, то в следующий раз, когда будут начисляться проценты, они начислятся на меньшую сумму. То есть обычно чем быстрее вы выплачиваете долг, тем меньше процентов вы заплатите поверх денег, которые занимали.
Существуют различные схемы выплат кредита. Можно выплачивать долг равными платежами, а можно выплачивать процент от оставшегося долга. Так как он уменьшается с каждой выплатой, то каждая новая выплата будет меньше. Тогда долг выплачивается неравными платежами.
МАТЕМАТИЧЕСКИЙ СМЫСЛ КРЕДИТА:
Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов. Каждый последующий год процент начисляется не на исходную сумму, а на исходную сумму, увеличенную предыдущим начислением процентов. Отсюда выходит формула начисления процента в задачах на кредит:
\(S_{n} = S_{0}\left( 1 + \frac{r}{100} \right)^{n}\)
\(где\ S_{n} - долг\ за\ период\ n\)
\(S_{0} - сумма,\ взятая\ в\ крдит,\)
\(r - процентная\ ставка\ кредита\)
\(n - количество\ месяцев\ или\ лет,\)
\(за\ которое\ расчитывается\ долг\)
Далее будет рассмотрено несколько простых подготовительных задач для понимания сути кредита и возможных вариантов выплат.
Наталья взяла в кредит 100 000 рублей в банк под 6% годовых на 3 года. Какую сумму Наталья должна будет вернуть банку через:
-
один год;
-
два года;
-
три года,
если за этот период она не выплачивала долг?
-
Рассчитаем по формуле сложного процента, какая станет сумма долга через один год:
\(S_{1} = 100\ 000\left( 1 + \frac{6}{100} \right) = 100\ 000 \bullet 1,06 = 106\ 000\)
-
Теперь посчитаем долг, который накопится за два года:
\(S_{2} = 100\ 000\left( 1 + \frac{6}{100} \right)^{2} = 100\ 000 \bullet {1,06}^{2} = 106\ 000 \bullet 1,06 = 112\ 360\)
-
Аналогично посчитаем долг через три года:
\(S_{3} = 100\ 000\left( 1 + \frac{6}{100} \right)^{3} = 112\ 360 \bullet 1,06 = 119\ 101,6\)
Ответ:\(\ 106\ 000\); \(112\ 360\); \(119\ 101,6\).
В декабре 2020 года планируется взять срочный кредит на 50 000 рублей под 20% в месяц. Первого числа каждого месяца, начиная с января, на долг начисляются проценты, а с 15 по 20 число каждого месяца погашают долг на 20 000 рублей. Сумма выплат в последнем месяце может быть меньше. В каком месяце долг будет полностью погашен?
-
Составим таблицу, в которую будем заносить состояние долга на первое число каждого месяца – когда начисляются проценты, и на оставшуюся часть года, когда выплачивается по 20 000:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Январь |
-
В декабре 2020 был взят кредит в 50 000, на который сразу в январе 1 числа начислили 20%. А до конца этого же месяца полученная сумма уменьшилась на 20 000. Занесем это в таблицу:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Январь | 50 000 ∙ 1,2 = 60 000 | 60 000 – 20 000 = 40 000 |
-
Сумма долга не равна нулю, значит 1 февраля на оставшуюся сумму начислят снова 20%:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Январь | \(50\ 000\ \bullet \ 1,2 = 60\ 000\) | \(60\ 000\ –20\ 000 = 40\ 000\) |
| Февраль | \(40\ 000\ \bullet \ 1,2 = 48\ 000\) |
И в течение месяца снова погасят долг на 20 000:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Январь | \(50\ 000\ \bullet \ 1,2 = 60\ 000\) | \(60\ 000\ –20\ 000 = 40\ 000\) |
| Февраль | \(40\ 000\ \bullet \ 1,2 = 48\ 000\) | \(48\ 000\ –20\ 000 = 28\ 000\) |
-
Аналогично 1 марта начислится 20%, а в течение месяца полученная сумма уменьшится на 20 000:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Февраль | \(40\ 000\ \bullet \ 1,2 = 48\ 000\) | \(48\ 000\ –20\ 000 = 28\ 000\) |
| Март | \(28\ 000\ \bullet \ 1,2 = 33\ 600\) | \(33\ 600\ –20\ 000 = 13\ 600\) |
-
И снова долг не равен нулю, значит он перейдет в апрель:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Март | \(28\ 000\ \bullet \ 1,2 = 33\ 600\) | \(33\ 600\ –20\ 000 = 13\ 600\) |
| Апрель | \(13\ 600\ \bullet \ 1,2 = 16\ 320\) |
И тогда последняя выплата будет меньше 20 000 и закроет весь оставшийся долг:
| Месяц | 1 число | 15 – 20 число |
|---|---|---|
| Март | \(28\ 000\ \bullet \ 1,2 = 33\ 600\) | \(33\ 600\ –20\ 000 = 13\ 600\) |
| Апрель | \(13\ 600\ \bullet \ 1,2 = 16\ 320\) | \(16\ 320\ –16\ 320 = 0\) |
Таким образом долг полностью будет погашен в апреле.
Конечно, кредит с такими большими начислениями – редкость, но и такое бывает. И нужно очень внимательно читать и интерпретировать условия кредита.
Ответ: апрель.
Олег взял в банке кредит на 100 тыс. рублей на 3 года под 10% годовых. В начале каждого года, начиная с года займа, начисляются процент по кредиту, а в течение этого года выплачивается часть долга. Олег был не очень хорошим заёмщиком, поэтому в течение первого года долг он не выплачивал совсем. В течение второго года он вернул банку 70 тыс. рублей, а в течение третьего года погасил долг полностью. Сколько тыс. рублей Олег вернул банку?
\(S_{2} = 100 \bullet \left( 1 + \frac{10}{100} \right)^{2} = 100 \bullet {1,1}^{2}\)
-
Уже в течение второго Олег отдал банку 70 тыс., то есть:
\(100 \bullet {1,1}^{2} - 70\)
-
В начале третьего года на эту сумму снова наложили 10%, после чего он выплатил некую сумму, которая обратила долг в ноль:
\(\left( 100 \bullet {1,1}^{2} - 70 \right) \bullet 1,1 - x = 0\)
Таким образом мы составили уравнение, в котором \(x\) – это количество тыс. рублей, которым Олег закрыл оставшийся долг. Решим это уравнение:
\(x = \left( 100 \bullet {1,1}^{2} - 70 \bullet \right)1,1\)
\(x = 100 \bullet {1,1}^{3} - 70 \bullet 1,1\)
\(x = 133,1 - 77 = 56,1\)
-
То есть Олег всего заплатил банку
\(70 + 56,1 = 126,1\ тыс.\ рублей\)
Ответ: 126,1.
Экономические задачи. Ценные бумаги
Задачи на ценные бумаги – это вид экономических задач, решение которых строится на понимании того, что такое ценные бумаги, и умении превратить это знание в математическую модель. Универсальной формулы, которая помогает решить любую задачу с ценными бумагами нет, так как в задачах обычно описана функция, по которой ценные бумаги растут. Также эти задачи могут комбинироваться с задачами по вкладам, так как вклад и ценные бумаги – два альтернативных способа увеличения своего капитала.
ЧТО ТАКОЕ ЦЕННАЯ БУМАГА:
Ценные бумаги обычно продают различные компании для того, чтобы привлечь деньги, на которые они будут развивать свой бизнес.
Если компания становится успешной и хорошо развивается, стоимость ценных бумаг может расти. Вы можете купить дешевую ценную бумагу, пока компания еще маленькая, рассчитывая на то, что, если она будет хорошо развиваться, стоимость этих ценных бумаг вырастет в несколько раз. Тогда их можно будет продать по их новой рыночной стоимости, несмотря на то, что вы купили ценную бумагу по меньшей цене.
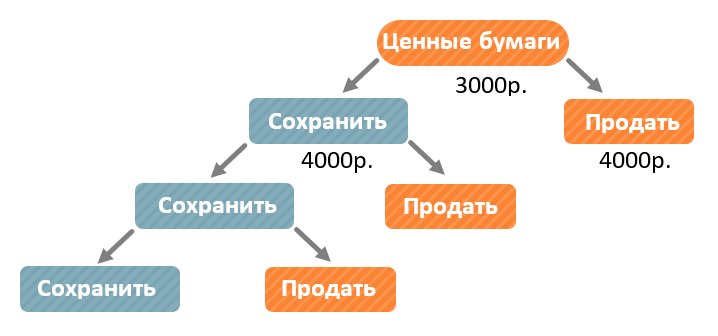
Таким образом вы можете совершать с ценными бумагами две операции:
-
Оставлять у себя ценную бумагу и ждать, пока она вырастет в цене.
-
Вы можете продать их обратно компании за бόльшую сумму, чем вы их покупали.
МАТЕМАТИЧЕСКИЙ СМЫСЛ ЦЕННЫХ БУМАГ:
Если у человека есть возможность продать ценные бумаги и положить их на вклад под определенный процент, то для экономистов стоит вопрос – когда именно продать ценную бумагу? Когда разница между разной стоимостью ценных бумаг станет меньше, чем фиксированные проценты с вклада?
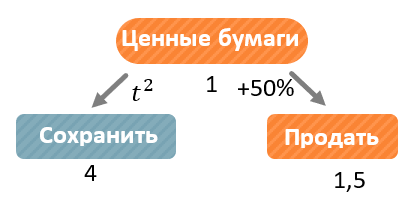
Стоимость ценных бумаг может расти в соответствии с какой-либо функцией. Например, стоимость бумаги равна \(t^{2}\) тыс. рублей, где \(t\) – это количество лет. То есть в первый год ценная бумага стоит 1 тыс. рублей, во второй 4 тыс. рублей, в третий 9 и так далее. То есть рост стоимости ценных бумаг дан как функция от проходящего времени.
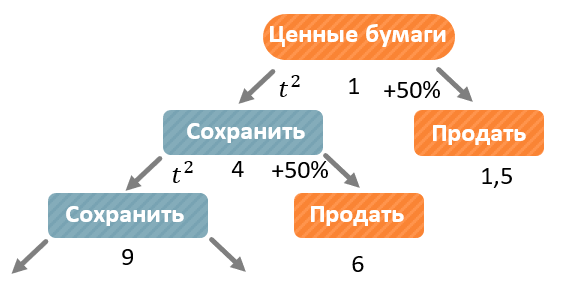
Катя купили ценные бумаги, стоимость которых равна \(t^{2}\) тыс. рублей в конце года \(t\) \((t = 1;2;\ldots)\). В конце любого года Катя может продать ценные бумаги и положить деньги, которые она с них получит, на вклад в банк под 50% годовых. В конце какого года Кате стоит продать ценные бумаги, чтобы получить наибольшую выгоду?
-
Для того чтобы понять, в какой момент выгоднее продавать ценные бумаги и класть деньги в банк, мы должны найти прибыль Кати за год, если она оставит ценную бумагу, и прибыль Кати за год, если она положит эти же деньги на вклад.
Составим схему, на которой будем отслеживать полученную разными способами прибыль за разные годы. В конце первого года стоимость ценой бумаги будет равна \(1^{1} = 1\). В этот момент мы можем её продать или оставить:
-
Будем рассматривать случай продажи и сохранения ценных бумаг и сразу считать, какую прибыль дадут оба этих действия через год.
В конце первого года:
-
Если Катя оставит ценные бумаги, то в конце второго года их стоимость будет равна \(t^{2} = 2^{2} = 4\);
-
Если Катя продаст ценные бумаги и положит их на вклад, то в конце второго года она получит \(1 \bullet 1,5 = 1,5\) тыс. рублей:
Очевидно, что продавать ценные бумаги в конце первого года не выгодно, так как через год они принесут больше прибыли, чем вклад.
-
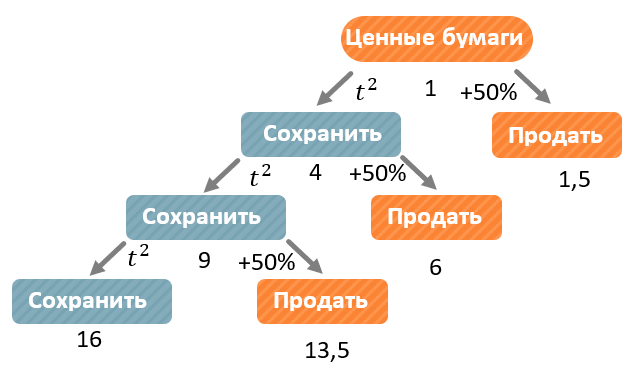
Теперь, мы можем продать ценные бумаги в конце второго года уже за 4 тыс. рублей и положить их на вклад или подождать, пока их цена дальше будет расти как \(t^{2}\).
В конце второго года:
-
Если их оставить, то в конце третьего года стоимость бумаг будет равна \(t^{2} = 3^{2} = 9\) тыс рублей;
-
Если их продать и положить на вклад, то в конце третьего года Катя получит \(4 \bullet 1,5 = 6\) тыс. рублей:
Снова прибыль от ценных бумаг больше, чем прибыль от вклада. Тогда в конце второго года ценные бумаги продавать не выгодно.
-
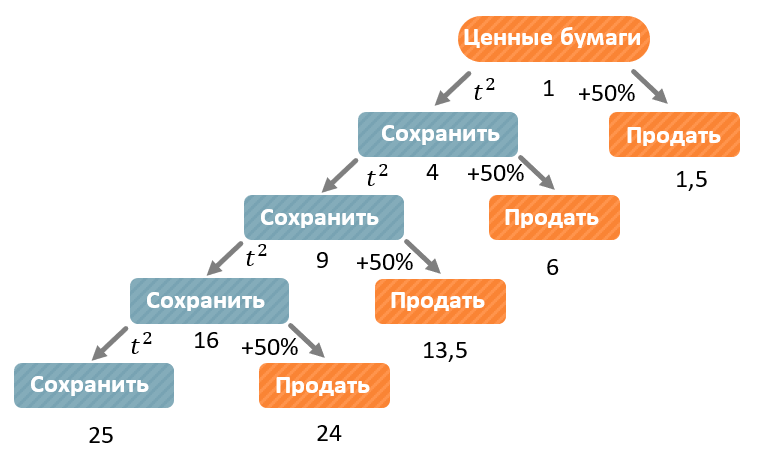
Аналогично рассмотрим ситуацию, когда встанет выбор о продаже ценных бумаг в конце третьего года:
-
Если оставить ценные бумаги, в конце четвертого года они будут стоить \(t^{2} = 4^{2} = 16\) тыс. рублей;
-
Если их продать, через год Катя получит \(9 \bullet 1,5 = 13,5\) тыс. рублей:
Продавать бумаги в конце третьего года не выгодно.
-
В конце четвертого года:
-
Если оставить ценные бумаги, через года они будут стоить \(t^{2} = 5^{2} = 25\) тыс. рублей;
-
Если продать и положить деньги на вклад, через год получится \(16 \bullet 1,5 = 24\) тыс. рублей:
-
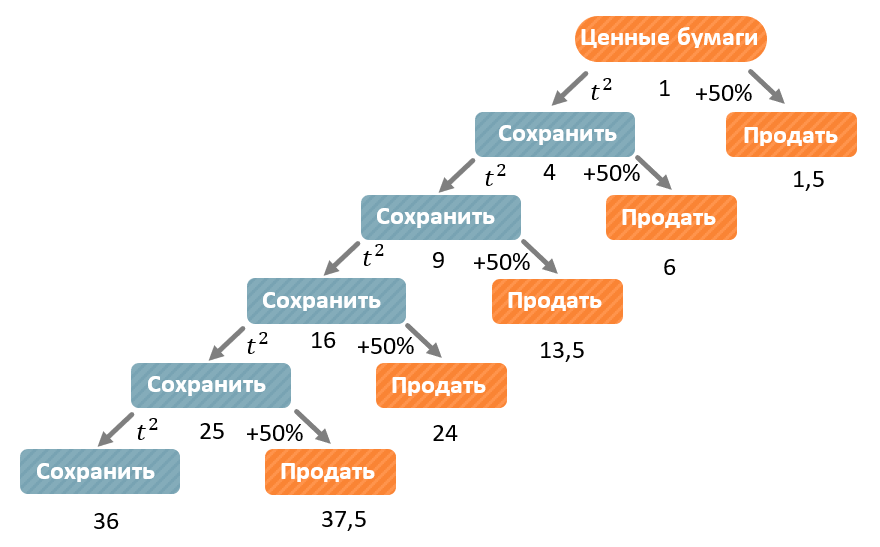
В конце пятого года:
-
Если оставить ценные бумаги, через год они будут стоить \(t^{2} = 6^{2} = 36\) тыс. рублей;
-
Если продать их и положить на вклад, через год Катя получит \(25 \bullet 1,5 = 37,5\) тыс. рублей:
Значит продавать ценные бумаги в конце пятого года – выгодно. Запишем ответ.
Ответ: 5.
Экономические задачи. Экономические показатели
Задачи с экономическими показателями – задания из блока «Экономические задачи», которые встречаются реже всего. От неготовности увидеть такие задачи возникают трудности при их решении. Здесь важно понимать, по каким принципам меняются экономические показатели, чтобы верно составить математическую модель.
ЧТО ТАКОЕ ЭКОНОМИЧЕСКИЕ ПОКАЗАТЕЛИ:
Экономические показатели – это собирательный термин для любых чисел, которые описывают экономическое положение чего-либо – уровень безработицы, средняя зарплата по региону, процент роста ВВП и т. д.
Всё, что может описать экономика, имеет свои экономические показатели. Перечислить их все невозможно. При решении экономических задач данного типа нужно руководствоваться бытовой логикой и понимать, как работает рост в процентах – то есть уметь работать со сложным процентом.
МАТЕМАТИЧЕСКИЙ СМЫСЛ ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ:
Помимо формулы сложного процента нужно знать, как находятся среднее арифметическое, так как в экономике часто используют средние показатели при оценке экономического роста:
\(a_{ср} = \frac{a_{1} + a_{2} + \ldots + a_{n}}{n} = \frac{\sum_{}^{}a}{n}\)
В регионе А в 2017 году средняя зарплата на душу населения была равна \(50\ 000\). Каждый год она росла на 15%. На сколько процентов изменился суммарный доход населения через два года в 2019 году, если каждый год из-за постоянных миграций население региона уменьшалась на 20%? Ответ округлите до целых.
-
Для начала разберемся с формулами.
Из определения среднего арифметического составим формулу средней зарплаты на душу населения:
\(средняя\ зарплата = \frac{суммарный\ доход\ населения}{количество\ жителей}\)
Значит, суммарный доход в определённый год будет равен:
\(суммарный\ доход\ населения = средняя\ зарплата \bullet количество\ жителей\)
-
Найдем суммарный доход за 2017 год. Средняя зарплата нам известна, а количество жителей – нет, тогда пусть \(x\) – количество жителей в 2017 году, получим:
\(суммарный\ доход\ 2017 = 50\ 000\ \bullet \ x\)
-
Теперь найдем суммарный доход уже через два года.
За это время средняя зарплата вырастет на 15% два раза, то есть будет равна:
\(средняя\ зарплата\ 2019 = \ 50\ 000\ \bullet {1,15}^{2} = 66125,\)
а количество жителей уменьшается на 20% два раза, то есть будет равно:
\(количество\ жителей\ 2019 = {0,8}^{2}x = 0,64\ x.\)
Подставим всё в общую формулу:
\(суммарный\ доход\ населения = 66125\ \bullet \ \ 0,64\ x = 42320\ x\)
-
Посчитаем, какую долю суммарный доход 2019 составляет от суммарного дохода 2017:
\(\frac{суммарный\ доход\ 2019}{суммарный\ доход\ 2017} = \frac{42320 \bullet x}{50\ 000\ x} = \frac{42\ 320}{50\ 000} = 0,8464\)
Переведём в проценты: \(0,8464 \bullet 100 = 84,64\)
Тогда изменение составит: \(100 - 84,64 = 15,36\)
Округлим до целых и запишем ответ.
Ответ: 15%.

Содержание