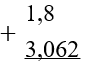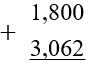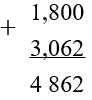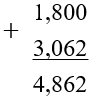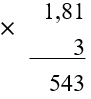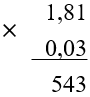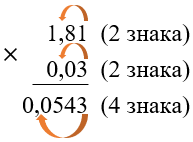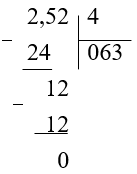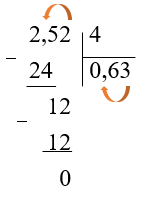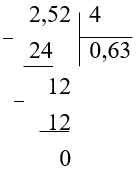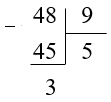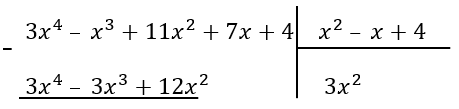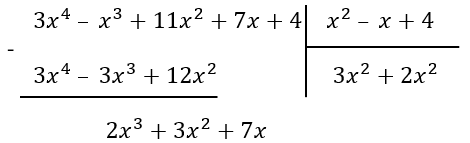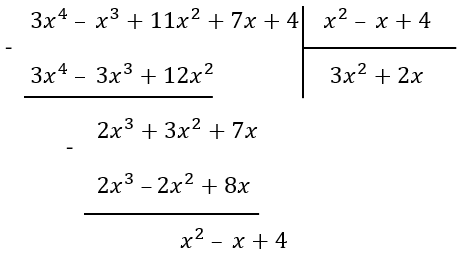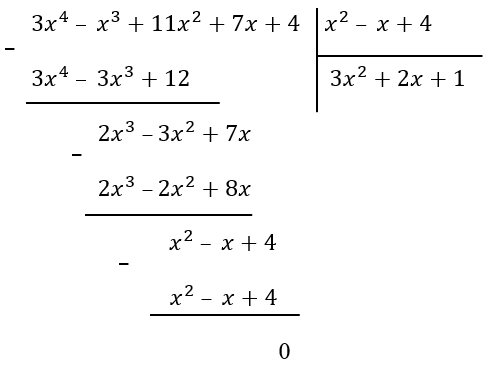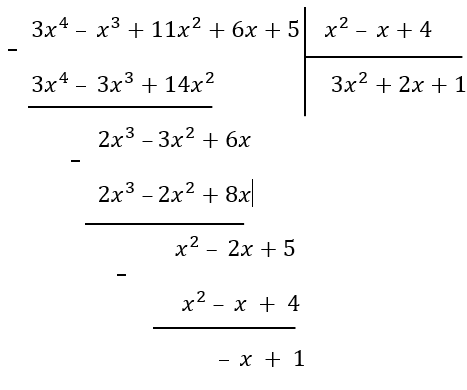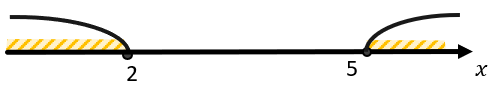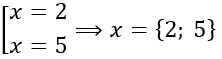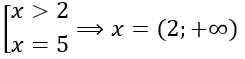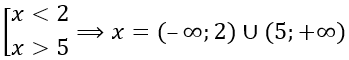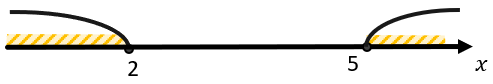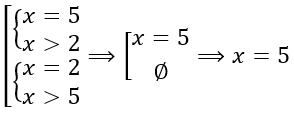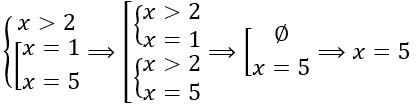Вычисления и уравнения
Десятичные дроби и действия с ними
Такие дроби принято записывать в строчку, а не как обыкновенную дробь.
ЗАПИСЬ ДЕСЯТИЧНОЙ ДРОБИ:
-
Сначала выделяют целую часть, ставят запятую, а потом записывают числитель дробной части.
Например:
\(7\frac{38}{100} = 7,38\)
-
Если дробь правильная, то целая часть равна 0:
Например:
\(\frac{6}{10} = 0,6\)
-
После запятой должно стоять столько цифр, сколько нулей стоит после единицы в знаменателе дроби. Например, если в знаменателе 10, то после запятой будет одна цифра.
-
Если в знаменателе 1000, то после запятой должно быть три цифры. Если в числителе дроби цифр меньше, чем нулей в знаменателе, тогда после запятой ставят нужное количество нулей, а уже потом записывают числитель:
Например:
\(\frac{56}{1000}\)
в знаменателе три нуля, а в числителе только две цифры. Чтобы уравнять количество цифр и нулей, представим дробь как
\(\frac{056}{1000}\)
Ноль в начале числителя никак на него не влияет, но помогает нам записать дробь в виде десятичной. Получается, что:
\(\frac{56}{1000} = \frac{056}{1000} = 0,056\)
ЧТЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ:
-
Читают десятичные дроби в соответствии с количеством цифр после запятой. Если цифра одна, то знаменатель соответствует числу 10. Тогда мы говорим, что доля десятичная. Если цифры две, то знаменатель соответствует числу 100, доля такой дроби – сотая. Так же называют тысячную долю, десятитысячную, миллионную и так далее.
Например:
\(19\frac{32}{100} = 19,32\) – девятнадцать целых, 32 сотых;
\(2\frac{9}{1000} = 2\frac{009}{1000} = 2,009\) – две целых, 9 тысячных;
\(\frac{3}{10} = 0,3\) – три десятых.
-
Если приписать или убрать ноль в конце дроби, то она не изменится.
Например:
\(0,80 = 0,8\) (80 сотых = 8 десятых);
\(0,0780 = 0,078\) (780 десятитысячных = 78 тысячных).
СРАВНЕНИЕ ДСЯТИЧНЫХ ДРОБЕЙ:
Чтобы сравнить дроби, их нужно привести к одинаковому количеству знаков после запятой.
Например:
Сравним 0,07 и 0,5.
У первой дроби после запятой две цифры, у второй только одна. Значит второй дроби нужно ее добавить так, чтобы дробь не изменилась. Мы можем приписать ноль в конце дроби.
Получим 0,07 и 0,50. Теперь мы сравниваем две дроби со знаменателем 100. Становится понятно, что 7<50, значит 0,07<0,50, значит 0,07<0,5.
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:
Сложим две десятичные дроби:
\(1,8 + 3,062\)
СПОСОБ 1:
-
Чтобы найти сумму или разность десятичных дробей, можно представить их как обыкновенные.
\(1\frac{8}{10} + 3\frac{62}{1000}\)
-
Если дроби имеют разные знаменатели, приведем их к одному. Проще всего приписать к одной дроби (и к числителю, и к знаменателю) одинаковое количество недостающих нулей:
\(1\frac{800}{1000} + 3\frac{62}{1000}\)
-
Теперь сложим дроби как смешанные:
\(1\frac{800}{1000} + 3\frac{62}{1000} = 4\frac{800 + 62}{1000} = 4\frac{862}{1000}\)
-
Переведем дробь обратно в десятичную:
\(4\frac{862}{1000} = 4,862\)
СПОСОБ 2:
-
Сумму или разность десятичных дробей можно найти столбиком. Запишем одно число под другим так, чтобы запятая одной дроби находилась по запятой другой:
-
Уравняем количество знаков (чисел) после запятой:
-
Сложим числа в столбик не обращая внимание на запятую.
-
Поставим запятую суммы под запятыми слагаемых:
СПОСОБ 3:
Можно воспользоваться тем фактом, что число состоит из целой и дробной частей и сложить сначала одно, потом другое.
-
Представим дроби в ином виде:
\(1,8 = 1 + 0,8\)
\(3,062 = 3 + 0,062\)
-
Сложим целые части:
\(1 + 3 = 4\)
-
Сложим дробные части:
\(0,8 + 0,062 = 0,862\)
-
Сложим полученные значения:
\(4 + 0,862 = 4,862\)
УМНОЖЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:
Умножение десятичной дроби на натуральное число:
Например:
\(1,81 \bullet 3\)
1. Чтобы умножить десятичную дробь на число, нужно найти их произведение в столбик, не обращая внимания на запятую:
2. В полученном произведении отделить запятой столько знаков справа, сколько отделено у дроби:
Умножение десятичной дроби на десятичную дробь:
Например:
\(1,81 \bullet 0,03\)
-
Чтобы умножить десятичную дробь на десятичную, нужно найти их произведение в столбик, не обращая внимания на запятую:
-
В полученном произведении отделить запятой столько знаков справа, сколько в сумме отделено у множителей:
Умножение десятичной дроби на 10, 100, 1000 и т.д.:
Чтобы умножить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков вправо, сколько нулей стоит в множителе после единицы.
Например:
\(2,34 \bullet 10 = 23,4\)
\(0,687 \bullet 1000 = 687\)
\(7,095 \bullet 100 = 709,5\)
Умножение десятичной дроби на 0,1, 0,01, 0,001 и т.д.:
Чтобы умножить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков влево, сколько знаков отделяет запятая в множителе:
\(183,7 \bullet 0,01 = 1,837\)
\(0,22 \bullet 0,1 = 0,022\)
\(619 \bullet 0,001 = 0,619\)
ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ:
Деление десятичной дроби на число:
Например:
\(2,52 : 4\)
-
Найдем частное в столбик, не обращая внимание на запятую:
-
В полученном частном отделим запятой столько знаков справа, сколько отделяется в делимом:
Деление десятичной дроби на десятичную дробь:
Например:
\(0,252 : 0,4\)
-
В делителе и делимом перенести вправо запятую на столько знаков, сколько их после запятой в делителе.
\(0,252 : 0,4 = 2,52 : 4\)
-
Выполнить деление на натуральное число.
Деление десятичной дроби на 10, 100, 1000 и т.д.:
Чтобы разделить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков влево, сколько знаков отделяет запятая в множителе.
-
Разделить на 10 = умножить на 0,1
-
Разделить на 100 = умножить на 0,01
-
Разделить на 1000 = умножить на 0,001
Деление десятичной дроби на 0,1, 0,01, 0,001 и т.д.:
Чтобы разделить десятичную дробь на такое число, нужно в десятичной дроби перенести запятую на столько знаков вправо, сколько нулей стоит в множителе после единицы.
-
Разделить на \(0,1\ =\) умножить на 10
-
Разделить на\(\ 0,01\ =\) умножить 100
-
Разделить на \(0,001\ = \ \)умножить на 1000
Обыкновенные дроби и действия с ними
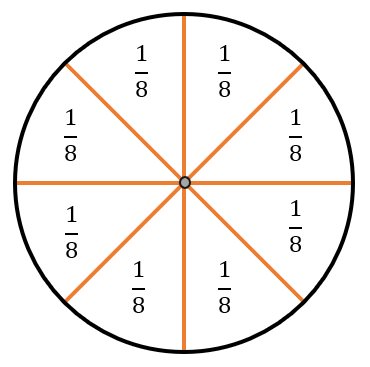
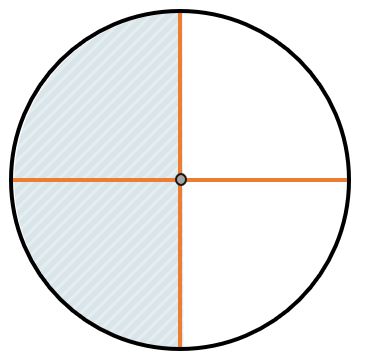
Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).
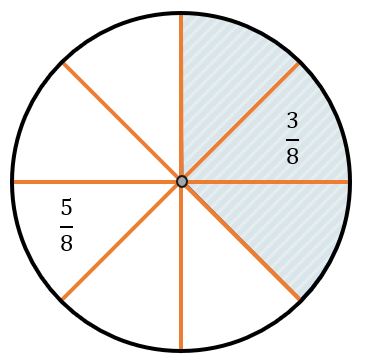
Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)
Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.
Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.
ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:
Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).
Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.
Например:
\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)
\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)
\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:
-
Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.
\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Например:
\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)
\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)
-
Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.
Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:
\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)
Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.
Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.
АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:
-
Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.
-
Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.
-
Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.
-
Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.
Например:
\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)
УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:
-
Обратные числа:
Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:
\(\frac{a}{1} = a : 1 = a\)
Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).
Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.
-
Умножение дробей:
Представим умножение дроби на число как сумму дробей:
\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)
Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:
\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)
-
Деление дробей:
Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.
Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:
\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)
Таким же образом делят дроби на дроби:
\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)
Смешанные дроби и действия с ними
Неправильная дробь – это дробь, числитель которой больше знаменателя. В таком случае у дроби выделяется целая часть и её можно записать в виде смешанной.
Например,
\(\frac{7}{4} = \frac{4}{4} + \frac{3}{4} = 1 + \frac{3}{4} = 1\frac{3}{4}\)
1 – целая часть, а \(\frac{3}{4}\) – дробная часть смешанного числа \(1\frac{3}{4}\).
АЛГОРИТМ ПЕРЕВОДА НЕПРАВИЛЬНОЙ ДРОБИ В СМЕШАННУЮ:
-
Разделить числитель на знаменатель в столбик с остатком.
-
Неполное частное будет целой частью.
-
Остаток (если он есть) станет числителем дробной части смешанной дроби, а делитель - знаменателем.
Например,
Переведем неправильную дробь \(\frac{48}{9}\) в смешанную:
Неполное частное \(= 5\), остаток \(= 3,\) делитель \(= 9\), тогда эту неправильную дробь можно записать как: \(5\frac{3}{9}\).
АЛГОРИТМ ПЕРЕВОДА СМЕШАННОЙ ДРОБИ В НЕПРАВИЛЬНУЮ:
-
Перемножить целую часть со знаменателем дробной части.
-
К полученному произведению прибавить числитель дробной части.
-
Записать полученную сумму в числитель неправильной дроби, а знаменатель оставить без изменений.
Например,
Переведем смешанную дробь \(4\frac{5}{7}\) в неправильную:
Числитель неправильной дроби будет равен
\((4 \bullet 7) + 5 = 28 + 5 = 33\).
Знаменатель останется прежний и будет равен 7.
Получим: \(4\frac{5}{7} = \frac{33}{7}\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ СМЕШАННЫХ ДРОБЕЙ:
При сложении и вычитании смешанных чисел отдельно складывают целые части, отдельно дробные по правилам сложения обыкновенных дробей.
-
Если суммой дробных частей является неправильная дробь, то из нее выделяют целую часть и прибавляют к сумме целых частей.
Например:
\(5\frac{3}{8} + 2\frac{6}{8} = (5 + 2) + (\frac{3}{8} + \frac{6}{8}) = 7 + \frac{9}{8} = 7 + 1\frac{1}{8} = 8\frac{1}{8}\)
-
Если при вычитании дробная часть уменьшаемого меньше дробной части вычитаемого, то поступают так:
\(7\frac{3}{5}\ –\ 2\frac{4}{5} = (7 + \frac{3}{5})\ –\ 2\frac{4}{5} = (6 + 1 + \frac{3}{5})\ –\ 2\frac{4}{5} = (6 + 1\frac{3}{5})\ –\ 2\frac{4}{5} = (6 + \frac{8}{5})\ –\ 2\frac{4}{5} = 6\frac{8}{5} + 2\frac{4}{5}\)
Таким образом мы выделили из целой части единицу и прибавили её к дробной. Теперь можно считать разность:
\(7\frac{3}{5}\ –\ 2\frac{4}{5} = 6\frac{8}{5} + 2\frac{4}{5} = (6\ –\ 2) + (\frac{8}{5}\ –\ \frac{4}{5}) = 4 + \frac{4}{5} = 4\frac{4}{5}\)
-
Так же поступают при вычитании смешанной дроби из целого числа.
Например:
\(3\ –\ 1\frac{2}{6} = (2 + \frac{6}{6})\ –\ 1\frac{2}{6} = (2\ –\ 1) + (\frac{6}{6}\ –\ \frac{2}{6}) = 1\frac{4}{6}\)
Линейные уравнения
С помощью преобразований его можно привести к виду \(\text{ax} = b\), где \(a \neq 0,\ b\) ‒ некоторые числа.
Для решения достаточно поделить обе части равенства на a: \(x = \frac{b}{a}\)
\(3\left( x - 5 \right) - 5 = - x\)
1. Приведем выражение к виду \(\text{ax} = b\). Для этого раскроем скобки и соберем слагаемые, содержащие переменные, с одной стороны равенства, а не содержащие – с другой:
\(3x - 15 - 5 = - x\ \)
\(3x - 20 = - x\ \)
\(4x - 20 = 0\ \)
\(4x = 20\)
2. Разделим обе части равенства на коэффициент при x:
\(x = 5\)
Ответ: 5
Уравнение будет линейным, даже если в нем присутствуют дроби. Главное, чтобы переменной не было в знаменателе.
\(\frac{x}{3} - 1 = \frac{5}{2}\)
1. Умножим обе части равенства на общий знаменатель дробей, входящих в уравнение, чтобы избавиться от дробей:
\(\left. \ \frac{x}{3} - 1 = \frac{5}{2} \right| \cdot 6\)
\(2x - 6 = 15\)
2. Приведем выражение к виду \(\text{ax} = b\):
\(2x = 21\)
3. Разделим обе части равенства на коэффициент при x:
\(x = 10,5\)
Ответ: 10,5
КОРНИ ЛИНЕЙНОГО УРАВНЕНИЯ
Количество корней уравнения зависит от коэффициентов a и b следующим образом:
1. При \(\mathbf{a}\mathbf{\neq 0}\):
\(ax\ = \ b\)
\(x\ = \ \frac{b}{a}\)
Один корень уравнения
Например:
\(5x\ = \ 10\)
\(x\ = \ \frac{10}{5}\)
\(x\ = \ 2\)
2. При \(\mathbf{a = 0,\ b \neq 0}\):
\(0x\ = \ b\)
\(x \neq \frac{b}{0}\)
Корней нет
3. При \(\mathbf{a = 0,\ }\mathbf{b}\mathbf{=}\mathbf{0}\):
\(0x = 0\)
Такое равенство соблюдается, когда \(x\) – любое число.
Квадратные уравнения
В общем виде оно выглядит следующим образом:
\(ax^{2} + bx + c = 0,\) где \(a \neq 0,\ b,\ c\) – некоторые числа.
ДИСКРИМИНАНТ:
Корни уравнения можно определить с помощью дискриминанта \(D = b^{2} - 4ac\) по формулам:
\(\left\lbrack \begin{matrix} \ \\ \ x_{1} = \frac{- b + \sqrt{D}\ }{2a} \\ \ \\ \ x_{1} = \frac{- b - \sqrt{D}\ }{2a}\ \\ \ \\ \end{matrix} \right.\ \)
- Если дискриминант больше нуля – уравнение имеет два корня.
- Если дискриминант равен нулю – уравнение имеет один корень.
- Если дискриминант меньше нуля – корней нет.
\(x^{2} = 6x\ –\ 5\)
-
Способ 1:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
\(x^{2}\ –\ 6x\ + 5 = 0\)
2. Определим дискриминант полученного уравнения:
\(D = 6^{2} - 4 \cdot 1 \cdot 5 = 16 = 4^{2}\)
3. С помощью дискриминанта найдем корни по формулам:
\(\left\lbrack \begin{matrix} \ \\ \ x_{1} = \frac{6 + 4\ }{2} \\ \ \\ \ x_{1} = \frac{6 - 4\ }{2}\ \\ \ \\ \end{matrix} \right.\ \) \(\left\lbrack \begin{matrix} x_{1} = 5 \\ {\text{\ \ \ }x}_{2} = 1 \\ \end{matrix} \right.\ \)
Ответ: 5; 1.
СОКРАЩЁННЫЙ ДИСКРИМИНАНТ:
Существует второй способ решения квадратного уравнения. В случае, если коэффициент \(b\) – четное число, запишем его как \(2k\). Квадратное уравнение примет следующий вид:
\(ax^{2} + 2kx + c = 0\),\(\ a \neq 0,\ k,\ c\) – некоторые числа.
Тогда вместо дискриминанта D будем использовать сокращённый дискриминант \(\frac{D}{4}\), а формула его нахождения будет следующей:
\(\frac{D}{4} = k^{2}\ –\ ac\)
Корни уравнения определим так же через сокращённый дискриминант:
\(\left\lbrack \begin{matrix} \ \\ \ x_{1} = \frac{- k + \sqrt{\frac{D}{4}}\ }{a} \\ \ \\ \ x_{1} = \frac{- k - \sqrt{\frac{D}{4}}\ }{a}\ \\ \ \\ \end{matrix} \right.\ \)
-
Способ 2:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
\(x^{2}\ –\ 6x\ + 5 = 0\)
2. Выделим коэффициент k:
\(x^{2}\ –\ 2 \bullet 3x\ + 5 = 0\)
\(k = 3\)
3. Определим сокращённый дискриминант полученного уравнения:
\(\frac{D}{4} = 3^{2} - 1 \cdot 5 = 4 = 2^{2}\)
4. С помощью сокращённого дискриминанта найдем корни по формулам:
\(\left\lbrack \begin{matrix} \ \\ \ x_{1} = \frac{3 + 2\ }{1} \\ \ \\ \ x_{1} = \frac{3 - 2\ }{1}\ \\ \ \\ \end{matrix} \right.\ \) \(\left\lbrack \begin{matrix} x_{1} = 5 \\ {\text{\ \ \ }x}_{2} = 1 \\ \end{matrix} \right.\ \)
Ответ: 5; 1.
Как мы видим, ответ остался прежним, но числа, используемые при вычислениях, стали меньше. Это значит, что при работе с большими коэффициентами решение через сокращённый дискриминант уменьшает вероятность вычислительной ошибки.
ТЕОРЕМА ВИЕТА:
В некоторых случаях (например, \(a = 1\)) корни проще искать по теореме Виета, решая подбором систему уравнений:
\(\left\{ \begin{matrix} \ \\ x_{1} \cdot x_{2} = \frac{c}{a}\ \\ \ \\ \text{\ \ \ \ \ \ x}_{1} + x_{2} = - \frac{b}{a}\ \\ \ \\ \end{matrix} \right.\ \)
Важно, что теорему Виета можно использовать при любом ненулевом коэффициенте а, формула представлена в общем виде. Однако если \(a = 1,\) то чаще всего нужно работать с целыми числами, а не с дробными, что упрощает подбор.
Следствия из теоремы Виета:
Используя теорему Виета, можно увидеть взаимосвязь между коэффициентами b и c и знаками корней уравнения.
Коэффициент c показывает, будут ли одинаковыми знаки корней:
-
Если\(\ c > 0\), то корни\(\ x_{1}\) и \(x_{2}\ \) имеют одинаковый знак.
-
Если коэффициент \(c < 0\), корни \(x_{1}\) и \(x_{2}\) будут разных знаков.
Коэффициент b показывает, какой именно знак у корней, если он один, либо какой корень положительный, а какой отрицательный, если знаки разные.
-
Если \(x_{1} + x_{2} = - b > 0\) (т.е. сумма корней положительна), то возможны 2 варианта:
а) либо оба корня положительны;
б) либо модуль положительного корня больше модуля отрицательного.
-
Если\(\ x_{1} + x_{2} = - \ b < 0\) (т.е. сумма корней отрицательна), то опять же есть 2 варианта:
а) либо все корни отрицательны;
б) либо модуль положительного корня меньше модуля отрицательного.
\(x^{2} - 5x + 6 = 0\)
1. Составим систему:
\(\left\{ \begin{matrix} \ \\ \ x_{1} \cdot x_{2} = 6 \\ \ \\ \text{\ \ \ }x_{1} + x_{2} = 5\ \\ \ \\ \end{matrix} \right.\ \)
Из следствий из т. Виета видим, что \(c > 0\), значит у корней одинаковые знаки.
Коэффициент \(b > 0\), значит оба корня положительные
2. Подберем \(x_{1},\ \ x_{2}\) так, чтобы оба равенства выполнялись.
Видим, что произведение больше нуля, значит, либо оба числа отрицательные, либо оба положительные. Сумма положительна, значит, оба положительные.
Произведение корней раскладываем всеми способами на множители:
\(6 = 2 \cdot 3 = 1 \cdot 6\)
Через сумму делаем проверку:
\(2 + 3 = 5\)
\(1 + 6 = 7\)
В данном случае подходят числа
\(x_{1} = 2,\ \ x_{2} = 3\).
Ответ: 2; 3.
ЧАСТНЫЕ СЛУЧАИ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ:
-
Если \(a + b + c = 0\), то \(x_{1} = 1,\ \ x_{2} = \frac{c}{a}\)
\(x^{2}\ + 3x\ –\ 4 = 0\)
1. Сложим все коэффициенты уравнения, чтобы проверить, является ли это уравнение примером частного случая. Действительно, коэффициенты в сумме дают 0:
\(1 + 3\ –\ 4 = 0\)
2. Тогда по правилу: \(x_{1} = 1,\ \ x_{2} = \frac{c}{a}\) получаем:
\(\left\lbrack \frac{x_{1} = 1}{x_{2} = \frac{–4}{1}\ = \ –4} \right.\ \)
Ответ: 1; -4.
-
Если \(a + c = b\), то \(x_{1} = \ –1,\ \ x_{2} = \ –\ \frac{c}{a}\)
\(x^{2}\ + 9x\ + 8 = 0\)
1. Сложим коэффициенты a и c, чтобы проверить уравнение на соответствие второму частному случаю. Действительно \(a + c = b\):
\(1 + 8 = 9\)
2. Тогда по правилу: \(x_{1} = \ –1,\ \ x_{2} = \ –\ \frac{c}{a}\) получаем:
\(\left\lbrack \frac{x_{1} = \ –1}{x_{2} = \ –\ \frac{8}{1}\ = \ –8} \right.\ \)
Ответ: – 1; – 8.
НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
Неполное квадратное уравнение вида
\(ax^{2} + bx = 0.\)
Если отсутствует свободный член, то:
1.Раскладываем левую часть на множители:
\(x(ax + b) = 0\)
2. Приравниваем каждый из множителей к нулю:
\(\left\lbrack \begin{matrix} \ \\ \begin{matrix} \ \\ x = 0 \\ ax + b = 0 \\ \ \\ \end{matrix} \\ \end{matrix} \right.\ \)
3. Решаем каждое из полученных уравнений, получаем:
\(\left\lbrack \begin{matrix} \ \\ x = 0 \\ x = - \frac{b}{a} \\ \end{matrix} \right.\ \)
Неполное квадратное уравнение вида
\(ax^{2} + c = 0.\)
Если отсутствует слагаемое с переменной в первой степени, то:
1.Делим левую и правую часть на коэффициент \(a \neq 0.\)
\(x^{2} + \frac{c}{a} = 0\)
2. Смотрим на знак слагаемого без переменной.
Если \(\frac{c}{a} < 0\), то раскладываем по формуле разности квадратов, приравниваем каждую из скобок к нулю и решаем полученные уравнения.
Если \(\frac{c}{a} = 0\), то получаем единственное решение \(x = 0.\)
Если \(\frac{c}{a} > 0\), то решений нет.
Уравнения высших степеней
Такие уравнения можно решать несколькими способами в зависимости от максимальной степени аргумента – высшей степени – и вида уравнения.
Важно отметить, что в первую очередь данное в условии уравнение полезно преобразовать, в частности – привести подобные слагаемые. Иногда сложные на первый взгляд уравнения после упрощений становятся квадратными или даже линейными.
Далее мы рассмотрим наиболее распространённые типы уравнений, которые имеют переменную в степени больше двух.
КУБИЧЕСКИЕ УРАВНЕНИЯ:
Кубические уравнения имеют такой общий вид:
\(\text{ax}^{3} + \text{bx}^{2} + \text{cx} + d = 0\), где \(a,\ b,\ c,\ d\) - некоторые числа, \(a \neq 0\)
-
1. Чаще всего удобно решать кубические уравнения через метод группировки.
Решим следующее уравнение таким методом:
\(x^{3} + x^{2}\ –\ 9x\ –9 = 0\)
1. Сгруппируем между собой слагаемые следующим образом:
\(\ {(x}^{3} + x^{2})\ (–\ 9x\ –9) = 0\)
\(x^{2}(x + 1)\ –\ 9(x + 1) = 0\)
2. Выделим общий множитель:
\((x + 1)(x^{2}–\ 9) = 0\)
3. Приравняем каждый множитель к нулю. Получим:
\(x + 1 = 0\) или \(x^{2}–\ 9 = 0\)
\(x = \ –1\)
\(x = 3\)
\(x = \ –3\)
Ответ: – 3; – 1; 3.
-
2. Существуют кубические уравнения, вид которых отличен от общего, но аргумент в третьей степени там так же присутствует.
Это уравнения вида:
\({(x + a)}^{3} = b\)
где a и b – какие-либо числа или выражения
Тогда мы решаем такие уравнения методом извлечения корня соответствующей степени.
Решим следующее уравнения таким методом:
\({(x + 6)}^{3} = 64\)
1. Извлечем корень третьей степени с каждой стороны уравнения:
\(\sqrt[3]{({x + 6)}^{3}} = \sqrt[3]{64}\)
\(x + 6 = 4\)
2. С помощью простейших алгебраических действий решим линейное уравнение:
\(x = 4\ –\ 6\)
\(x = - 2\)
Ответ: –2.
Аналогично решаются и другие подобные уравнения высших степеней нечетной кратности (если степень 3,5,7 и далее). Уравнения с четной степенью решаются похожим образом через извлечение корня соответствующей степени, однако в таком случае появляется модуль и необходимо рассматривать два уравнения в совокупности.
УРАВНЕНИЯ ЧЕТВЕРТОЙ СТЕПЕНИ:
Как видно из названия, старшая степень таких уравнений – четвертая. Они имеют вид:
\(\text{ax}^{4} + \text{bx}^{3} + cx^{2} + dx + e = 0\), где \(a,\ b,\ c,\ d,\ e\) - некоторые числа, \(a \neq 0\)
Если в уравнении четвертой степени коэффициенты при третьей и первой степени равны нулю, то такие уравнения называются биквадратными и имеют вид:
\(\text{ax}^{4} + \text{bx}^{2} + c = 0\)
Такие уравнения решаются методом замены:
1. Пусть \(x^{2} = t\), получим:
\(\text{at}^{2} + bt + c = 0\)
2. Решим обычное квадратное уравнение, получим два корня – t1 и t2.
3. Проведем обратную замену:
\(\left\lbrack \frac{x = \pm {\sqrt{t}}_{1}}{x = \pm {\sqrt{t}}_{2}} \right.\ \)
Решим следующее уравнение таким методом:
\({3x}^{4}\ –\ 8x^{2}\ –\ 3 = 0\)
1. Пусть \(x^{2} = t\):
\({3t}^{2}\ –\ 8t\ –\ 3 = 0\)
2. Решим квадратное уравнение:
\(D = 64\ –\ 4 \bullet (–3) \bullet 3 = 64 + 36 = 10^{2}\)
\(t_{1\ } = \ \frac{8 + 10}{6} = 3\)
\(t_{2\ } = \ \frac{8\ –10}{6} = \ –\frac{1}{3}\)
3. Сделаем обратную замену:
\(x^{2} = 3\); \(x = \pm \sqrt{3}\)
\(x^{2} = \ –\ \frac{1}{3}\) – корней нет
Ответ: – \(\sqrt{3}\); \(\sqrt{3}\).
ДЕЛЕНИЕ МНОГОЧЛЕНА НА ВЫРАЖЕНИЕ:
При работе с уравнениями большой степени иногда нужно понизить степень для удобства вычислений, либо уравнение дробно-рациональное и имеет и в числителе, и в знаменателе многочлены высокой степени. В таком случае можно поделить одно выражение на другое в столбик, используя те же правила, что и при делении обычных чисел, например:
\(\frac{{3x}^{4}\ –\ x^{3} + 11x^{2} + 7x + 4}{x^{2}\ –\ x + 4}\)
1. Поделим первое слагаемое делимого на первое слагаемое делителя, получим первое слагаемое для нашего частного. Теперь перемножим полученное слагаемое \((3x^{2})\) с делителем:
\(3x^{2}{(x}^{2}\ –\ x + 4\)) = \({3x}^{4}\ –\ {3x}^{3} + 12x^{2}\)
2. Вычтем из делимого получившийся многочлен. Теперь будем делить первое слагаемого этой разности на делитель, аналогично первому пункту. Снова перемножим слагаемое с делителем
\(2x{(x}^{2}\ –\ x + 4)\) = \(2x^{3}\ –2x^{2} + 8x\)
3. Видим, что теперь разность равна самому делителю, значит последнее слагаемое частного будет равно 1:
4. Теперь получаем более простое выражение:
\(\frac{{3x}^{4}\ –\ x^{3} + 11x^{2} + 7x + 4}{x^{2}\ –\ x + 4} = {3x}^{2} + 2x + 1\)
ДЕЛЕНИЕ МНОГОЧЛЕНА НА ВЫРАЖЕНИЕ С ОСТАТКОМ:
Если мы немного изменим делитель, чтобы получить, например, вот такое выражение:
\(\frac{{3x}^{4}\ –\ x^{3} + 11x^{2} + 6x + 5}{x^{2}\ –\ x + 4}\)
То мы уже не получим ноль в конце решения в столбик. У нас появится остаток:
Остаток запишем следующим образом:
делимое = (делитель) х (частное) + (остаток)
В данном случае:
\({3x}^{4}\ –\ x^{3} + 11x^{2} + 6x + 5 =\)
\((x^{2}\ –\ x + 4)(\ {3x}^{2} + 2x + 1)\ –\ x\ + \ 1\)
Дробно - рациональные уравнения
Данный тип уравнений отличается тем, что содержит в знаменателе выражение с переменной. Поэтому может возникнуть опасная ситуация – переменная примет такое значение, что знаменатель обратится в ноль. Чтобы этого не произошло, заранее исключим из рассмотрения нули знаменателя и определяем область допустимых значений.
АЛГОРИТМ РЕШЕНИЯ ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ:
\(\frac{1}{x - 2} = \frac{2}{x + 4}\)
1. Определим область допустимых значений:
\(\left\{ \begin{matrix} \ \\ \ x - 2 \neq 0 \\ \ \\ \ x + 4 \neq 0\ \\ \end{matrix}\text{\ \ \ \ \ \ \ \ }\left\{ \begin{matrix} \ \\ \ x \neq 2 \\ \ \\ \ \ \ x \neq - 4 \\ \end{matrix} \right.\ \right.\ \)
То есть решением данного уравнения может быть любое число кроме 2 и ‒4.
2. Умножим обе части равенства на общий знаменатель всех дробей и сократим одинаковые выражения в числителе и знаменателе там, где это возможно:
\(\left. \ \frac{1}{x - 2} = \frac{2}{x + 4}\ \right| \cdot (x\ –2)\left( x\ + 4 \right)\)
\(\frac{(x\ –2)\left( x\ + 4 \right)}{x - 2} = \frac{2(x\ –2)\left( x\ + 4 \right)}{x + 4}\)
\(x + 4 = 2(x\ –2)\)
3. Упрощаем уравнение с помощью разрешенных преобразований:
\(x + 4 = 2x\ –4\)
4. Определяем тип получившегося уравнения (линейное, квадратное или кубическое) и решаем подходящим методом. В данном случае видим линейное уравнение. Переносим иксы в одну сторону, числа в другую:
\(8 = x\)
5. Проверяем полученный корень (корни) на принадлженость к области допустимых значений. Корень принадлежит ОДЗ, если при его подстановке в уравнение знаменатели не обращаются в ноль:
Ответ: 8.
\(\frac{x - 3}{x - 5} + \frac{1}{x} = \frac{x + 5}{x\left( x - 5 \right)}\)
1. Определим область допустимых значений:
\(\left\{ \begin{matrix} \ \\ \ x - 5 \neq 0 \\ \ \\ \ x \neq 0 \\ \ \\ \ \ \ \ x(x - 5) \neq 0\ \\ \end{matrix}\text{\ \ \ \ \ }\left\{ \begin{matrix} \ \\ \ x \neq 5 \\ \ \\ \ \ x \neq 0\ \\ \end{matrix} \right.\ \right.\ \)
2. Умножим обе части равенства на общий знаменатель всех дробей и сократим одинаковые выражения в числителе и знаменателе там, где это возможно:
\(\left. \ \frac{x - 3}{x - 5} + \frac{1}{x} = \frac{x + 5}{x\left( x - 5 \right)} \right| \cdot x\left( x - 5 \right)\)
\(\frac{\left( x - 3 \right)x\left( x - 5 \right)}{x - 5} + \frac{x\left( x - 5 \right)}{x} = \frac{x\left( x + 5 \right)\left( x - 5 \right)}{x\left( x - 5 \right)}\)
\(\left( x - 3 \right)x + x - 5 = x + 5\)
3. Упрощаем уравнение с помощью разрешенных преобразований:
\(x^{2} - 3x + x - 5 = x + 5\)
\(x^{2} - 2x - 5 - x - 5 = 0\)
\(x^{2} - 3x - 10 = 0\)
4. Определяем тип получившегося уравнения (линейное, квадратное или кубическое) и решаем подходящим методом. В данном случае получилось квадратное уравнение, причем коэффициент при \(x^{2}\) равен 1. Значит, удобно использовать теорему Виета:
\(\left\{ \begin{matrix} \ \\ \text{\ \ \ }x_{1} \cdot x_{2} = - 10 \\ \ \\ x_{1} + x_{2} = 3\ \\ \end{matrix} \right.\ \)
Подходит пара чисел -2 и 5.
5. Исключаем те значения корней, которые обращают в ноль знаменатель, то есть не входят в область допустимых значений (ОДЗ).
Ответ: ‒2
При подстановке корней в уравнение должно получиться верное равенство. Это свойство можно использовать для проверки полученных ответов.
Системы и совокупности уравнений с одной переменной
СИСТЕМА:
Ключевым моментом в решении систем уравнений является понимание самой сути системы. Система означает, что необходимо учитывать решения нескольких уравнений или нескольких неравенств при записи решения. То есть нужно решить и первое, и второе уравнение/неравенство, ответом самой системы будет пересечение этих ответов.
Рассмотрим несколько простейших систем.
\(\left\{ \begin{matrix} x = 2 \\ x = 5 \\ \end{matrix} \right.\ \Longrightarrow \varnothing\)
Решением системы являются все значения переменной, при которых выполняются все перечисленные условия. Может ли x одновременно равняться и 2, и 5? Нет, поэтому у этой системы решений нет.
Часто системы усложняются неравенствами.
\(\left\{ \begin{matrix} x > 2 \\ x = 5 \\ \end{matrix} \right.\ \Longrightarrow x = 5\)
В этой системе требуется, чтобы x был одновременно и равен 5, и был больше 2. При каких значениях это возможно? Только при \(x = 5\).
Рассмотрим ещё одну систему:
\(\left\{ \begin{matrix} x < 2 \\ x > 5 \\ \end{matrix} \right.\ \Longrightarrow \varnothing\)
Мы видим 2 отрезка, у которых нет пересечения, поэтому корней данная система не имеет.
СОВОКУПНОСТЬ:
Также иногда вам придётся работать с совокупностью. Совокупность предполагает вариативность: может выполняться ИЛИ то, ИЛИ другое условие.
Например:
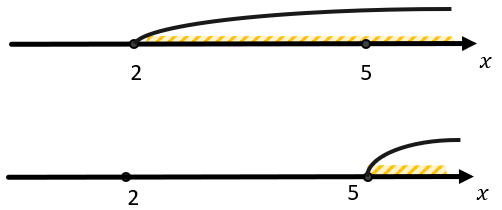
В ответ пойдут обе точки: и 2, и 5. Обратите внимание, что если у нас в ответе конечное количество точек, то их принято писать в фигурных скобочках.
Там подходят или 5, или те x, которые больше 2. Но 5 больше 2, значит, нам просто подходит промежуток от 2 до бесконечности.
Здесь мы будем рассматривать объединение: если x является корнем хотя бы одного уравнения, неравенства из совокупности, значит, он уже является решением.
КОМБИНАЦИИ СИСТЕМ И СОВОКУПНОСТЕЙ:
Но и это ещё не всё. Иногда совокупность включает в себя систему или система включает себя совокупность. Давайте посмотрим.
Такая ситуация называется «совокупность двух систем». То есть в ответ пойдут все x, которые удовлетворяют первой системе, и все x, которые удовлетворяют второй системе. Поэтому для того, чтобы её решить, нужно сначала решить внутренние системы, а затем в ответ написать все полученные в них корни.
Следующий пример немного другой:
Итак, у нас есть система. Это означает, что должно выполняться 2 условия:
1. x должен быть больше 2.
2. x должен быть равен либо 1, либо 5.
В таких случаях необходимо рассмотреть каждый корень из второго условия на соответствие первому, то есть перейти к совокупности двух систем.
Простейшие неравенства
Неравенства используются для сравнения чисел и выражений. Можно сравнивать числа и делать вывод об их расположении на числовой прямой относительно друг друга. Неравенство \(7 > 5\) означает, что число 7 лежит правее числа 5 на координатной оси:
Так же можно сравнивать самые разные выражения, например
\(x \geq 5\), или \(x^{2} + 2x > 4x + 5\).
В таком случае говорят о множестве решений неравенства, то есть о всех значениях переменной, для которой данное неравенство выполняется (в некоторых случаях это множество может состоять из одной точки или вообще быть пустым).
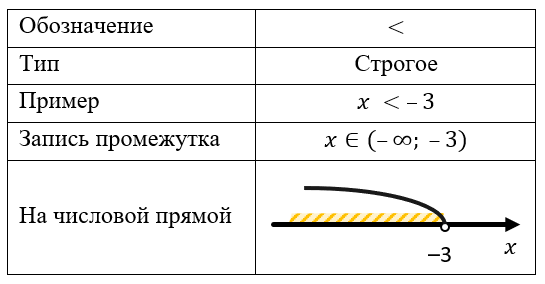
ОБОЗНАЧЕНИЕ НЕРАВЕНСТВ:
Неравенства можно обозначать четырьмя способами:
-
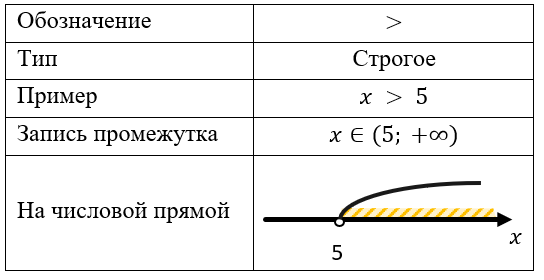
Больше
-
Меньше
-
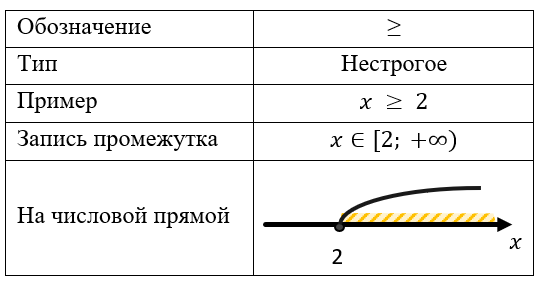
Больше или равно:
-
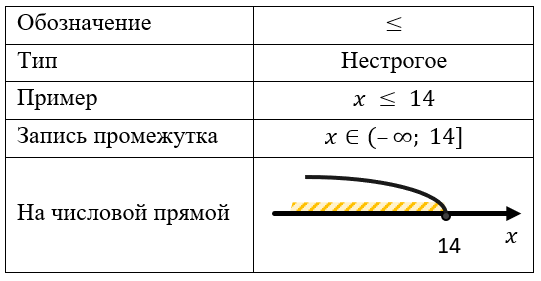
Меньше или равно:
Если неравенство строгое, то граничная точка в решение не входит (поэтому ее «выкалывают» на координатной оси).
У нестрого неравенства граничная точка в решение входит.
ДВОЙНЫЕ НЕРАВЕНСТВА:
Виды двойных неравенств не отличаются от видов обыкновенных, разница лишь в том, что промежуток обозначается уже двумя числами, а не одним.
Например:
\(1 < x \leq 4\)
Эта запись обозначает, что x больше 1 и при этом меньше либо равно 4.
1. Числовой промежуток будет записываться в соответствии со строгостью знаков к определенным числам. Скобка возле числа 1 будет круглой, а возле числа 4 – квадратной:
\(x \in (1;4\rbrack\)
2. Аналогично строгости знаков и виду скобок на числовой прямой будут закрашены или не закрашены точки. Число 1 будет отмечаться выколотой точкой, а число 4 закрашенной. Тогда на координатной прямой это двойное неравенство будет выглядеть так:
ПРАВИЛА ПРЕОБРАЗОВАНИЯ НЕРАВЕНСТВ:
1. Любое слагаемое в неравенстве можно перенести из одной части уравнения в другую, изменив его знак на противоположный:
\({x + 5 > 0 }{x > \ –5}\)
2. Можно умножать и делить левую и правую части уравнения на одно и то же положительное число:
\({2y > \left. \ 16 \right| : 2 }{y > 8}\)
3. Можно умножать и делить левую и правую части уравнения на одно и то же отрицательное число, заменяя при этом знак неравенства на противоположный:
\({–\frac{t}{2} \leq \left. \ 10 \right| \bullet \left( –2 \right) }{t \geq \ –20}\)
4. Для двойных неравенств соблюдаются те же правила, с разницей в том, что алгебраические преобразования производятся сразу над всеми его частями:
\({2 \leq x + 5 \leq 8 }{–3 \leq x \leq 3}\)
5. Как и в уравнениях можно раскрывать скобки и упрощать выражения во всех частях неравенства или, наоборот, раскладывать на множители.
Решить неравенство:
\(5(1\ –\ x) < 12\)
1. Преобразуем неравенства так, чтобы с одной стороны было только выражение, содержащее переменную, а с другой только число:
\(5(1\ –\ x) < 12\)
\(5\ –\ 5x < 12\)
\(–5x < 7\)
2. Делим на коэффициент перед переменной, при необходимости меняя знак на противоположный:
\(–5x < \left. \ 7 \right| : (–5)\)
\(x > \ –1,4\)
Ответ: \(x \in (–1,4; + \infty)\).
Рациональные неравенства
МЕТОД ИНТЕРВАЛОВ:
Для решения рациональных неравенств применяется метод интервалов. Рассмотрим его алгоритм:
-
Переносим все слагаемые влево.
-
Раскладываем левую часть на множители.
-
Приравняем каждый множитель к нулю и выразим переменную. Эти значения переменной являются нулями функции.
-
Отмечаем на координатной оси нули числителя и знаменателя (если он есть). Нули знаменателя всегда «выколотые» точки.
-
Ноль функции, полученный из множителя, стоящего в четной степени, образует «петлю» на координатной прямой.
-
Определяем знак неравенства в крайнем правом промежутке (можно подставить пробную точку из каждого промежутка в преобразованное неравенство).
-
Определяем знаки в остальных промежутках, двигаясь справа налево. Для соседних промежутков, включая петлю, знаки чередуются.
-
Выбираем нужные промежутки и записываем ответ.
Решите неравенство:
\(x^{2} + 8x\ –\ 5 \geq \ –5\)
1. Переносим все слагаемые влево:
\(x^{2} + 8x\ –\ 5 \geq \ –5\)
\(x^{2} + 8x\ –\ 5\ + 5 \geq 0\)
\(x^{2} + 8x \geq 0\)
2. Раскладываем левую часть на множители:
\(x^{2} + 8x \geq 0\)
\(x(x + 8) \geq 0\)
3. Чтобы найти нули неравенства, нужно приравнять каждый множитель к 0. Получившиеся значения отметим на координатной прямой. Точки будут выколотыми или закрашенными в соответствии со строгостью знака неравенства:
\(x\left( x + 8 \right) \geq 0\)
\(x = 0\ \ или\ \ x = \ –8\)
4. Мы получили три интервала. Нам нужно найти те интервалы, на которых x будет обращать неравенство в верное. Определим знак неравенства в самом крайнем промежутке. В этот промежуток входят все числа больше, либо равные 0. Допустим, \(x = \ 1\), тогда
\(x\left( x + 8 \right) = \ 1(1 + 8) = 9\)
9 – число положительное. Значит на самом крайнем промежутке x будет обращать выражение \(x\left( x + 8 \right)\ \)в положительное число:
5. Все промежутки справа налево будут менять знак, переходя через точки 0 и –8. Поэтому получаются следующие знаки промежутков:
6. Неравенство \(x\left( x + 8 \right) \geq 0\) должно быть больше, либо равно нулю. Значит решением такого неравенства будут положительные промежутки:
\(x \in (–\infty;\ –8\rbrack \cup \lbrack 0; + \infty)\)
Ответ: \(x \in (–\infty;\ –8\rbrack \cup \lbrack 0; + \infty)\).
Решите неравенство:
\({4x}^{2} + 20x + 25 > 0\)
1. Все слагаемые уже перенесены влево.
2. Разложим левую часть на множители. Здесь мы видим ФСУ – квадрат суммы:
\({4x}^{2} + 20x + 25 > 0\)
\({(2x + 5)}^{2} > 0\)
3. Найдем нули функции:
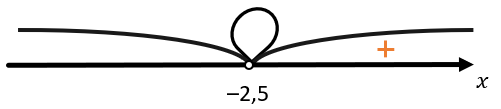
\({\left( 2x + 5 \right)^{2} = 0 }{2x + 5 = 0 }{2x = \ –5 }{x = \ –2,5}\)
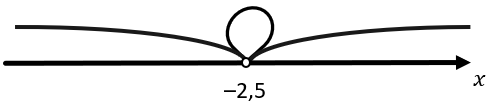
Если один из множителей стоит в четной степени, то ноль функции, образованный приравниванием этого множителя к нулю, образует «петлю». Эта петля – промежуток, который включает в себя одно число – именно этот ноль функции, в данном случае «петля» равна – 2,5:
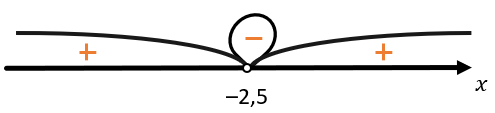
4. Таким образом у нас появилось три промежутка. Отметим знак самого правого из них. Для удобства представим, что x = 0, т.к. 0 как раз входят в этот промежуток:
\({(2x + 5)}^{2} = 5^{2} = 25\)
25 – положительное число, значит и промежуток является положительным:
5. При переходе через ноль функции знак поменяется именно в петле. Тогда для самого левого промежутка знак снова станет положительным:
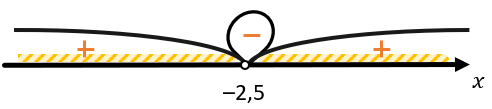
6. Выберем промежутки, которые обращают наше выражение в положительное:
\(x \in (–\infty;–2,5) \cup (–2,5; + \infty)\)
То есть наше выражение обращается в неположительное, только если \(x = \ –2,5.\ \ \)Поэтому число \(–2,5\ \)– единственное число, которое не идет в ответ.
Ответ: \(x \in (–\infty;–2,5) \cup (–2,5; + \infty)\).
Решим неравенство:
\(\frac{x^{2}(x\ –\ 5)}{x\ –\ 8} \leq 0\)
1. Так как пункты 1 и 2 алгоритма уже выполнены, сразу переходим к пункту 3:
Нули числителя: \(x = 0\ и\ x = 5\ \ \)
Нули знаменателя: \(x = 8\)
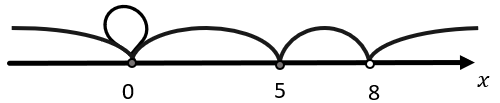
Отмечаем полученные точки на координатной прямой. Нули числителя будут закрашиваться в соответствии со знаком неравенства, а нули знаменателя всегда выколоты, независимо от знака.
При этом 0 на координатной прямой образует петлю аналогично примеру №2, потому что ноль функции \(x = 0\ \)был найден через множитель \(x^{2}\):
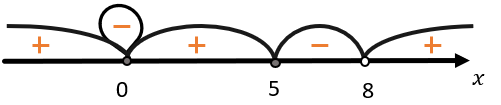
2. В крайнем правом промежутке можно рассмотреть точку \(x = 10:\)
\(\frac{x^{2}(x\ –\ 5)}{x\ –\ 8} = \frac{10^{2}(10\ –\ 5)}{10\ –\ 8} = \frac{100 \bullet 5}{2} = 250\)
После подстановки получаем, что выражение больше 0.
3. Определяем знаки в оставшихся промежутках с учетом петли:
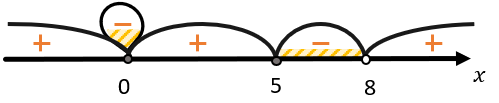
4. Необходимо отметить промежутки, которые обращают выражение в отрицательное число или равно нулю:
т.к. само число 0 обращает всё выражение в 0, то оно тоже подходит для ответа:
\(x \in \left\{ 0 \right\} \cup \lbrack 5;8)\)
Ответ: \(x \in \left\{ 0 \right\} \cup \lbrack 5;8)\).

Содержание